2023-2024学年北京市海淀区师达中学数学八年级第一学期期末学业水平测试模拟试题含答案

这是一份2023-2024学年北京市海淀区师达中学数学八年级第一学期期末学业水平测试模拟试题含答案，共8页。试卷主要包含了下列因式分解结果正确的是，下列二次根式，最简二次根式是，点P等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
考生须知：
1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)
1．近期，受不良气象条件影响，我市接连出现重污染天气，细颗粒物（PM2.5）平均浓度持续上升，严重威胁人民群众的身体健康，PM2.5是直径小于或等于2.5微米（1微米相当于1毫米的千分之一）的颗粒物，可直接进入肺部把2.5微米用科学记数法表示为（ ）
A．2.5×10﹣6米B．25×10﹣5米
C．0.25×10﹣4米D．2.5×10﹣4米
2．在实数，0，，506，，中，无理数的个数是（ ）
A．2个B．3个C．4个D．5个
3．小军同学在网格纸上将某些图形进行平移操作，他发现平移前后的两个图形所组成的图形可以是轴对称图形.如图所示，现在他将正方形从当前位置开始进行一次平移操作，平移后的正方形的顶点也在格点上，则使平移前后的两个正方形组成轴对称图形的平移方向有( )
A．3个B．4个C．5个D．无数个
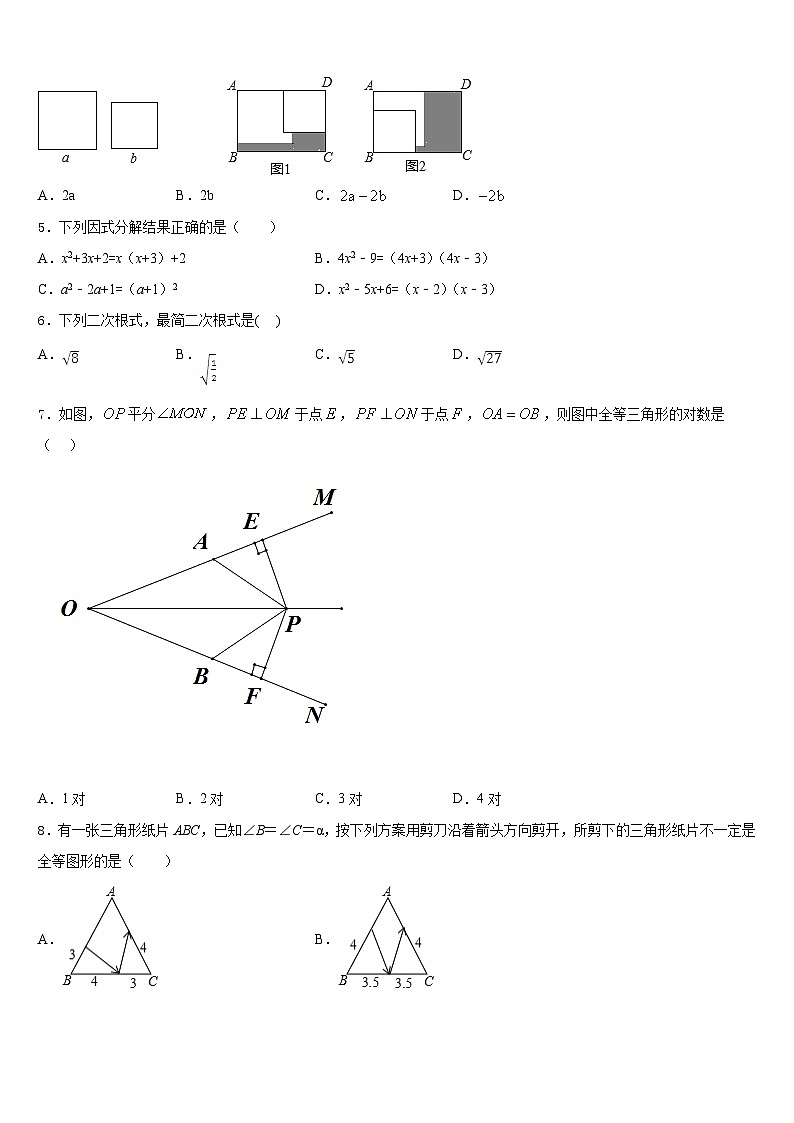
4．在矩形ABCD内，将两张边长分别为a和的正方形纸片按图1，图2两种方式放置图1，图2中两张正方形纸片均有部分重叠，矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为，图2中阴影部分的面积为当时，的值为
A．2aB．2bC．D．
5．下列因式分解结果正确的是（ ）
A．x2+3x+2=x（x+3）+2B．4x2﹣9=（4x+3）（4x﹣3）
C．a2﹣2a+1=（a+1）2D．x2﹣5x+6=（x﹣2）（x﹣3）
6．下列二次根式，最简二次根式是( )
A．B．C．D．
7．如图，平分，于点，于点，，则图中全等三角形的对数是（ ）
A．1对B．2对C．3对D．4对
8．有一张三角形纸片ABC，已知∠B＝∠C＝α，按下列方案用剪刀沿着箭头方向剪开，所剪下的三角形纸片不一定是全等图形的是（ ）
A．B．
C．D．
9．点P（1，﹣2）关于y轴对称的点的坐标是（ ）
A．（1，2）B．（﹣1，2）C．（﹣1，﹣2）D．（﹣2，1）
10．如图，在等腰中，，是斜边的中点，交边、于点、，连结，且，若，，则的面积是( )
A．2B．2.5C．3D．3.5
二、填空题(每小题3分,共24分)
11．如图，在△ABC 中，AB=AC=12，BC=8， BE 是高，且点 D、F 分别是边 AB、BC 的中点，则△DEF 的周长等于_____________________．
12．已知关于的方程无解，则m=________．
13．如图，已知点D、点E分别是等边三角形ABC中BC、AB边的中点，AD=5，点F是AD边上的动点，则BF+EF的最小值为______．
14．如图，在△ABC中，AB=AC=24厘米，BC=16厘米，点D为AB的中点，点P在线段BC上以4厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．当点Q的运动速度为_______厘米/秒时，能够在某一时刻使△BPD与△CQP全等．
15．如图，等边的边长为，则点的坐标为__________．
16．如图，在中，,，的垂直平分线与交于点，与交于点，连接.若，则的长为____________.
17．观察表格，结合其内容中所蕴含的规律和相关知识可知b=__________；
18．若关于，的方程组的解是，则__________．
三、解答题(共66分)
19．（10分）如图，已知A（﹣4，﹣1），B（﹣5，﹣4），C（﹣1，﹣3），△ABC经过平移得到的△A′B′C′，△ABC中任意一点P（x1，y1）平移后的对应点为P′（x1+6，y1+4）．
（1）请在图中作出△A′B′C′；
（2）写出点A′、B′、C′的坐标；
（3）求△ABC的面积．
20．（6分）某公司开发的960件新产品必须加工后才能投放市场，现有甲、乙两个工厂都想加工这批产品，已知甲工厂单独加工48件产品的时间与乙工厂单独加工72件产品的时间相等，而且乙工厂每天比甲工厂多加工8件产品，在加工过程中，公司需每天支付50元劳务费请工程师到厂进行技术指导.
(1)甲、乙两个工厂每天各能加工多少件产品？
(2)该公司要选择既省时又省钱的工厂加工产品，乙工厂预计甲工厂将向公司报加工费用为每天800元，请问：乙工厂向公司报加工费用每天最多为多少元时，有望加工这批产品？
21．（6分）某县教育行政部门为了了解八年级学生每学期参加综合实践活动的情况，随机抽样调查了该县八年级学生一个学期参加综合实践活动的天数，并用得到的数据绘制了下面两幅不完整的统计图(如图)．
请你根据图中提供的信息，回答下列问题：
（1）求出参加抽样调查的八年级学生人数，并将频数直方图补充完整．
（2）在这次抽样调查中，众数和中位数分别是多少?
（3）如果该县共有八年级学生人，请你估计“活动时间不少于天”的大约有多少人？
22．（8分）（1）在如图所示的平面直角坐标系中表示下面各点：
A（0，3）；B（5，0）；C（3，﹣5）；D（﹣3，﹣5）；E（3，5）；
（2）A点到原点的距离是 ；
（3）将点C向x轴的负方向平移6个单位，它与点 重合；
（4）连接CE，则直线CE与y轴是什么位置关系；
（5）点D分别到x、y轴的距离是多少．
23．（8分）化简:
(1)(-2ab)(3a2-2ab-4b2);
(2)3x(2x-3y)-(2x-5y)·4x.
24．（8分）王华由，，，，，这些算式发现：任意两个奇数的平方差都是8的倍数
（1）请你再写出两个（不同于上面算式）具有上述规律的算式；
（2）请你用含字母的代数式概括王华发现的这个规律（提示：可以使用多个字母）；
（3）证明这个规律的正确性.
25．（10分）如图，在△ABC中，AD是BC边上的高，BE平分∠ABC交AC边于E，两线相交于F点．
（1）若∠BAC=60°，∠C=70°，求∠AFB的大小；
（2）若D是BC的中点，∠ABE=30°，求证：△ABC是等边三角形．
26．（10分）将矩形ABCD绕点A顺时针旋转α（0°＜α＜360°），得到矩形AEFG．
（1）如图，当点E在BD上时．求证：FD＝CD；
（2）当α为何值时，GC＝GB？画出图形，并说明理由．
参考答案
一、选择题(每小题3分,共30分)
1、A
2、A
3、C
4、B
5、D
6、C
7、C
8、D
9、C
10、B
二、填空题(每小题3分,共24分)
11、1
12、－3或1
13、5
14、4或6
15、
16、1
17、1
18、1
三、解答题(共66分)
19、（1）见解析；（2）A′（2，3）、B′（1，0）、C′（5，1）；（3）.
20、 (1)甲工厂每天加工16件产品，则乙工厂每天加工24件；(2)乙工厂向公司报加工费用每天最多为1225元时，有望加工这批产品.
21、（1）调查的初一学生人数200人；补图见解析；（2）中位数是4（天），众数是4（天）；（3）估计“活动时间不少于5天”的大约有2700人．
22、（1）作图见解析；（2）1 ；（1）D ；（4）平行 ；（5）点D到x轴的距离是5 ； 点D到y轴的距离是1
23、 (1) -6a3b+4a2b2+8ab3；(2) -2x2+11xy.
24、（1），；（2）；（3）见解析.
25、（1）115°；（2）证明见解析
26、 (1)见解析;(2)见解析.
列举
猜想与发现
3，4，5
32=4+5
5，12，13
52=12+13
7，24，25
72=24+25
…
…
17，b，c
172=b+c