数学九年级上册21.2.3 因式分解法教课ppt课件

这是一份数学九年级上册21.2.3 因式分解法教课ppt课件，共22页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂检测，两个因式的积等于零，至少有一个因式为零，解法一因式分解得，平方差公式，开方得等内容，欢迎下载使用。

1.理解用因式分解法解方程的依据.2.会用因式分解法解一元二次方程.3.会根据方程的特点选用恰当的方法解一元二次方程.
我们已经学过哪些解一元二次方程的方法?
直接开平方法，配方法，公式法.
多项式的因式分解有哪些方法？
ma + mb + mc = m(a+ b+ c);a2 ±2ab+b2=(a ± b)2；a2 -b2=(a + b)(a-b).
根据物理学规律，如果把一个物体从地面以10 m/s的速度竖直上抛，那么物体经过x s离地面的高度(单位：m)为 10x－4.9x2.根据上述规律，物体经过多少秒落回地面(结果保留小数点后两位)?
设物体经过x s落回地面，这时它离地面的高度为0 m， 即 10x－4.9x2＝0. ①
问题：请用用配方法或公式法解方程① .
∵ a=4.9,b=-10,c=0.
∴ b2－4ac = (－10)2－4×4.9×0 =100.
公式法解方程10x-4.9x2=0.
配方法解方程10x-4.9x2=0.
10x-4.9x2=0.
除配方法或公式法以外，能否找到更简单的方法解方程①？
知识点1 用因式分解法解方程
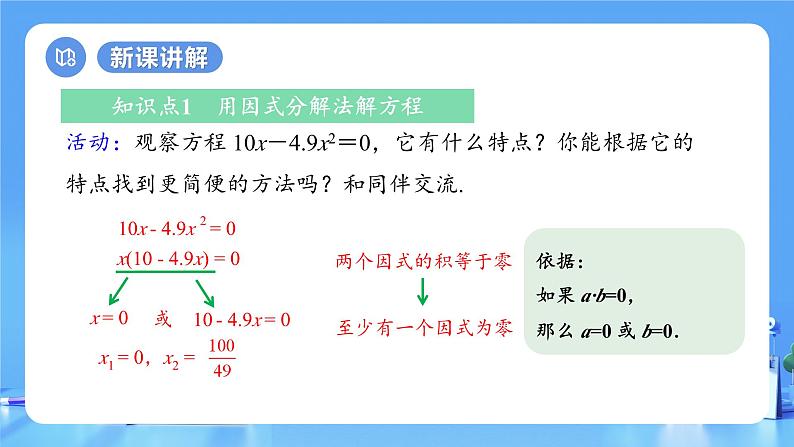
活动：观察方程 10x－4.9x2＝0，它有什么特点？你能根据它的特点找到更简便的方法吗？和同伴交流.
10x - 4.9x 2 = 0
x1 = 0，x2 =
或　10 - 4.9x = 0
x(10 - 4.9x) = 0
依据：如果 a·b=0，那么 a=0 或 b=0．
思考：解方程10x－4.9x2＝0时，二次方程是如何降为一次的？
可以发现，上面的解法中，不是用开平方降次，而是先因式分解，使方程化为两个一次式的乘积等于0的形式，再使这两个一次式分别等于0，从而实现降次．这种解一元二次方程的方法叫做因式分解法．
因式分解法的依据：如果 a·b=0，那么 a=0 或 b=0．
例1 解方程：x(x－2)＋x－2＝0．
解法一用到了整体思想，解法二用到了十字相乘法．
(x－2)(x＋1)＝0．
于是得x－2＝0，或x＋1＝0，
∴x1＝2，x2＝－1．
解法二：整理，得x2－x－2＝0，
因式分解，得(x－2)(x＋1)＝0．
解：移项、合并同类项，得4x2－1＝0．
因式分解，得(2x＋1)(2x－1)＝0．
于是得2x＋1＝0，或2x－1＝0，
用因式分解法解一元二次方程的步骤
注意：不能随意在方程两边约去含未知数的代数式，如x(x－1)＝x，若约去x，则会丢失x＝0这个根．
1．移项：将方程的右边化为0；
2．分解：将方程的左边分解为两个一次式的乘积；
3．转化：令每个一次式分别为0，得到两个一元一次方程；
4．求解：解这两个一元一次方程，它们的解就是一元二次方程的解．
知识点2 用适当的方法解一元二次方程
活动 和同伴交流，用适当的方法解下列方程：(1) 3x(x + 5)= 5(x + 5)； (2) (5x + 1)2 = 1；
即 3x − 5 = 0 或 x + 5 = 0.
分析：该式左右两边可以提取公因式，所以用因式分解法解答较快.
解：化简 (3x − 5) (x + 5) = 0.
分析：方程一边以平方形式出现，另一边是常数，可用直接开平方法.
解：开平方,得 5x + 1 = ±1.
(3) x2 − 12x = 4 ; (4) 3x2 = 4x + 1.
解：化为一般形式 3x2 - 4x - 1 = 0. ∵Δ=b2 - 4ac = 28 > 0,
分析：二次项系数为1，一次项系数为偶数，可用配方法来解题较快.
解：配方，得 x2 − 12x + 62 = 4 + 62,即 (x − 6)2 = 40.
分析：二次项的系数不为1，且不能直接开平方，也不能直接因式分解，所以适合公式法.
若一元二次方程可化为 (mx+n)2=p(m≠0，p≥0) 的形式，则宜选用直接开平方法； 若一元二次方程的二次项系数为 1，一次项系数为偶数，则宜选用配方法； 若一元二次方程整理后右边为 0，且左边能进行因式分解，则宜选用因式分解法； 若直接开平方法、配方法、因式分解法都不简便，则宜选用公式法.
如果 a · b =0，那么a=0或b=0.
将方程左边因式分解，右边=0.
因式分解的方法有ma + mb + mc = m(a+ b+ c);a2 ±2ab+b2=(a ± b)2；a2 -b2=(a + b)(a-b).
1．移项；2．分解；3．转化；4．求解
1．下列方程，最适合用因式分解法解的是（　　）A．(x－1)(x－2)＝3 　 　 　　 B．2(x－1)2＝x2－1C．x2＋2x－1＝0 　　　　　 D．x2＋4x＝2
解析：选项A，整理得x2－3x－1＝0，方程左边不能进行因式分解，故不适合；选项B，原方程可化为2(x－1)2＝(x＋1)(x－1)，移项后方程左边可提取公因式(x－1)，能进行因式分解；选项C，方程左边不能进行因式分解，故不适合；选项D，整理得x2＋4x－2＝0，方程左边不能进行因式分解，故不适合．
3．解下列方程：（1） （2）
解：（1）化为一般式x2－2x＋1＝0．因式分解，得(x－1)(x－1)＝0．∴x－1＝0，∴x1＝x2＝1．
(2x＋11)(2x－11)＝0．
∴2x＋11＝0，或2x－11＝0，
4．由多项式乘法：(x＋a)(x＋b)＝x2＋(a＋b)x＋ab，将该式从右到左使用，即可得到“十字相乘法”进行因式分解的公式：x2＋(a＋b)x＋ab＝(x＋a)(x＋b)．示例：分解因式：x2＋5x＋6＝x2＋(2＋3)x＋2×3＝(x＋2)(x＋3)．（1）尝试．分解因式：x2＋6x＋8＝(x＋ )(x＋ )；
（2）应用． 请用上述方法解方程：x2－3x－4＝0．
解：（2）∵x2－3x－4＝x2＋(－4＋1)x＋(－4)×1＝(x－4)(x＋1)＝0，
∴x－4＝0，或x＋1＝0，
∴x1＝4，x2＝－1．