人教版7年级下学期数学期末测试卷09

这是一份人教版7年级下学期数学期末测试卷09，共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1．在实数、、0、、3.1010010001…（相邻两个1之间的0依次增加1个）中，无理数的个数为（ ）
A．2个B．3个C．4个D．5个
2．下列各图中，∠1与∠2是对顶角的是（ ）
A．B．C．D．
3．下列命题是真命题的是( )
A．同角的补角相等
B．两条直线被第三条直线所截，同位角相等
C．两个无理数的和仍是无理数
D．有公共顶点且相等的两个角是对顶角
4．直线，将正按如图方式放置，点在直线上，若，则的度数是（ ）
A．B．C．D．
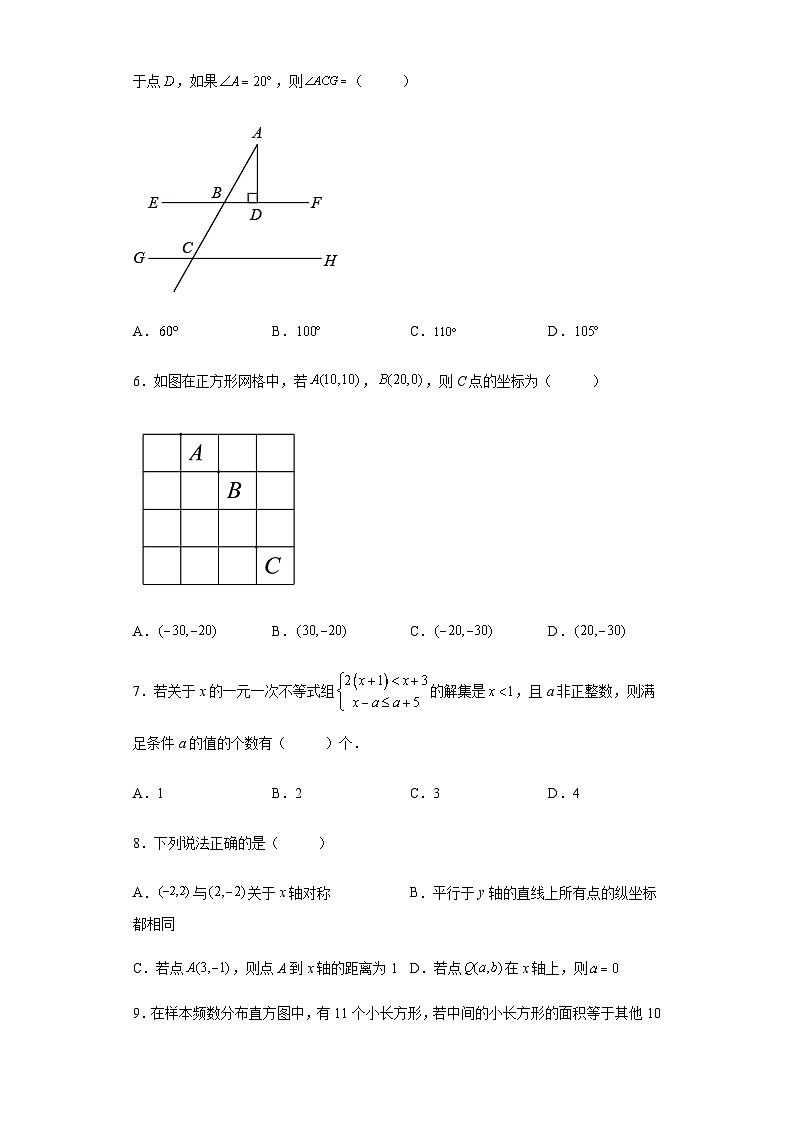
5．如图所示，直线，射线分别交直线，于点和点，于点，如果，则（ ）
A．B．C．D．
6．如图在正方形网格中，若，，则C点的坐标为（ ）
A．B．C．D．
7．若关于x的一元一次不等式组的解集是，且a非正整数，则满足条件a的值的个数有（ ）个．
A．1B．2C．3D．4
8．下列说法正确的是（ ）
A．与关于x轴对称B．平行于y轴的直线上所有点的纵坐标都相同
C．若点，则点A到x轴的距离为1D．若点在x轴上，则
9．在样本频数分布直方图中，有11个小长方形，若中间的小长方形的面积等于其他10个小长方形面积之和的，且中间一组的频数为40，则样本容量为（ ）
A．0.2B．160C．0.25D．200
10．如果a>b，那么下列不等式不成立的是( )
A．a-5> b-5B．-5a>-5b
C．D．-5a<-5b
11．已知方程组则x＋y的值为（ ）
A．8B．15C．－6D．
12．下列调查中，最适宜采用普查方式的是（ ）
A．对全国初中学生视力状况的调查B．了解江苏省义务教育阶段男女学生比例情况
C．旅客上飞机前的安全检查D．了解某种品牌手机电池的使用寿命
13．已知，，且，则的值为（ ）
A．2或8B．2或-8C．-2或8D．-2或-8
14．下列说法：①立方根等于它本身的数有，0，1；②负数没有立方根；③；④任何正数都有两个立方根，且它们互为相反数；⑤平方根等于它本身的数有0和1，正确的个数是（ ）
A．1个B．2个C．3个D．4个
15．定义一种新运算：，则不等式组的负整数解有（ ）
A．1个B．2个C．3个D．4个
二、填空题
16．正数a的平方根是和m，则________．
17．如图，将面积为5的三角形沿方向平移至三角形的位置，平移的距离是边长的两倍，那么图中的四边形的面积为____________．
18．已知直线轴，点的坐标为，并且线段，则点的坐标为__________．
19．某市为进一步加快文明城市的建设，园林局尝试种植A、B两种树种．经过试种后发现，种植A种树苗a棵，种下后成活了棵，种植B种树苗b棵，种下后成活了（b-2）棵．第一阶段两种树苗共种植40棵，且两种树苗的成活棵树相同，则种植A种树苗_________棵．第二阶段，该园林局又种植A种树苗m棵，B种树苗n棵，若m=2n，在第一阶段的基础上进行统计，则这两个阶段种植A种树苗成活棵数_________种植B种树苗成活棵数（填“＞”“＜”或“＝”）．
20．以方程组的解为坐标的点在第_____________象限．
三、解答题
21．（1）解方程组
（2）解不等式组，并把它的解集在数轴上表示出来．
22．如图，CE平分，F为CA延长线上一点，交AB于点G，，，求的度数．
23．为庆祝中国共产党建党100周年，某中学开展“学史明理、学史增信、学史崇德、学史力行”知识竞赛，现随机抽取部分学生的成绩分成A、B、C、D、E五个等级进行统计，并绘制成两幅不完整的统计图，请根据图中提供的信息，解答下列问题：
(1)本次调查中共抽取______名学生；
(2)补全条形统计图；
(3)在扇形统计图中，求B等级所对应的扇形圆心角的度数；
(4)若该校有1000名学生参加此次竞赛，估计这次竞赛成绩为A和B等级的学生共有多少名？
24．在平面直角坐标系中，A、B、C三点的坐标分别为（-6，7）、（-3，0）、（0，3）．
(1)画出△ABC；
(2)在△ABC中，点C经过平移后的对应点为C′（5，4），将△ABC作同样的平移得到△A′B′C′，画出平移后的△A′B′C′，并写出点 A′的坐标 ；
(3)P（-3，m）为△ABC 中一点，将点P 向右平移4个单位后，再向下平移7个单位得到点Q（n，-3），则 m＝ ，n＝ ．
25．某超市从厂家购进A、B两种型号的水杯，两次购进水杯的情况如下表：
(1)求每个A种型号的水杯和每个B种型号的水杯各多少元；
(2)该超市决定再次购进A、B两种型号的水杯共600个，总费用不超过15200元，那么该超市这次最少可以购进多少个A种型号的水杯？
26．
(1)填空：如图①，AB∥CD，猜想∠BPD与∠B，∠D的关系，并说明理由．
解：过点P作EF∥AB，如图所示
∴∠B＋∠BPE=180°（______________________________）．
∵AB∥CD，AB∥EF
∴EF∥CD（如果两条直线都和第三条直线平行，那么（_____________________）．
∴∠EPD＋∠D=180°
∴∠B＋∠BPE＋∠EPD＋∠D=________，
即∠BPD＋∠B＋∠D=360°
(2)仿照上面的解题方法，观察图②，已知AB∥CD，猜想图中∠BPD与∠B，∠D的关系，并说明理由．
(3)观察图③和④，已知AB∥CD，猜想图中∠BPD与∠B，∠D的关系，不需要说明理由．
进货批次
A型水杯（个）
B型水杯（个）
总费用（元）
一
100
200
8000
二
200
300
13000
答案
1．A
2．C
3．A
4．C
5．C
6．B
7．C
8．C
9．D
10．B
11．A
12．C
13．D
14．A
15．B
16．
17．20
18．或．
19． 22 >
20．四
21.解：（1）
由②得：，
将③代入①得：，
解得:
将代入③得：，
故方程组的解为：
（2）
解不等式①得：
解不等式②得：
故不等式组的解集为，
解集在数轴上表示如下：
22.解：∵CE平分，
∴，，
∵，
∴，
∵，
∴，
故的度数是25°．
23.(1)解：（人）．
本次调查中共抽取名学生．
(2)解：等级的人数为：，
等级的人数为：．
故补全条形统计图如下：
(3)解：，
．
答：等级所对应的扇形的圆心角的度数为．
(4)解：（人）．
答：这次竞赛成绩和等级的学生共有名．
24.(1)如图，△ABC即为所求；
(2)如图，△A′B′C′即为所求，A′（﹣1，8）；
(3)∵P(-3,m)为△ABC中一点，将点P向右平移4个单位后，再向下平移7个单位得到点Q(n,-3)，
∴n=﹣3+4=1，m-7=﹣3，
∴n=1，m=4．
故答案为：4，1．
25.(1)设每个A种型号的水杯和每个B种型号的水杯各x元，y元．
根据题意 得，
解得
答：每个A种型号的水杯和每个B种型号的水杯各20元，30元．
(2)设该超市这次可以购进m个A种型号的水杯．
根据题意 得．
解得．
答：该超市这次最少可以购进280个A种型号的水杯．
26.(1)过点P作EF∥AB，如图所示：
∴∠B+∠BPE=180°（两直线平行，同旁内角互补），
∵AB∥CD，EF∥AB，
∴CD∥EF（如果两条直线都和第三条直线平行，那么这两条直线也互相平行），
∴∠EPD+∠D=180°，
∴∠B+∠BPE+∠EPD+∠D=360°，
∴∠B+∠BPD+∠D=360°．
故答案为：两直线平行，同旁内角互补；这两条直线互相平行；360°．
(2)猜想∠BPD=∠B+∠D；
理由：过点P作EP∥AB，如图所示：
∵EP∥AB，
∴∠B=∠BPE（两直线平行，内错角相等），
∵AB∥CD，EP∥AB，
∴CD∥EP（如果两条直线都和第三条直线平行，那么这两条直线也互相平行），
∴∠EPD=∠D，
∴∠BPD=∠B+∠D．
(3)图③结论：∠D=∠BPD+∠B，
理由是：过点P作EP∥AB，如图所示：
∵EP∥AB，
∴∠B=∠BPE（两直线平行，内错角相等），
∵AB∥CD，EP∥AB，
∴CD∥EP（如果两条直线都和第三条直线平行，那么这两条直线也互相平行），
∴∠EPD=∠D，
∴∠BPD=∠B+∠D；
图④结论∠B=∠BPD+∠D，
过点P作EP∥AB，如图所示：
理由是：∵EP∥AB，
∴∠B=∠BPE（两直线平行，内错角相等），
∵AB∥CD，EP∥AB，
∴CD∥EP（如果两条直线都和第三条直线平行，那么这两条直线也互相平行），
∴∠EPD=∠D，
∴∠B=∠BPD+∠D．