人教版数学 九下 第29章 投影与视图 单元精选能力测试卷

人教版数学 九下 第29章 投影与视图

单元九下能力测试卷

一．选择题（共30分）

1.圆锥的主视图与左视图都是边长为的等边三角形，则圆锥的侧面展开图扇形的圆心角是

1.  B.  C.  D.

2.如图为一根圆柱形的空心钢管，它的主视图是

1.                   B.
   C.                 D.

3.如图，一个正方体纸盒的六个面上填有不同的数或式，从不同方向看到的情形如图所示，如果相对两个面上的数或式的值互为相反数，则的值为(   )

A.1 B.-1 C.0 D.2022

4.如图，夜晚，小亮从点A处经过路灯C的正下方沿直线走到点B处，他的影长y随他与点A之间的距离x的变化而变化，那么表示y与x之间的函数关系的图象大致为(   )

A. B. C D.

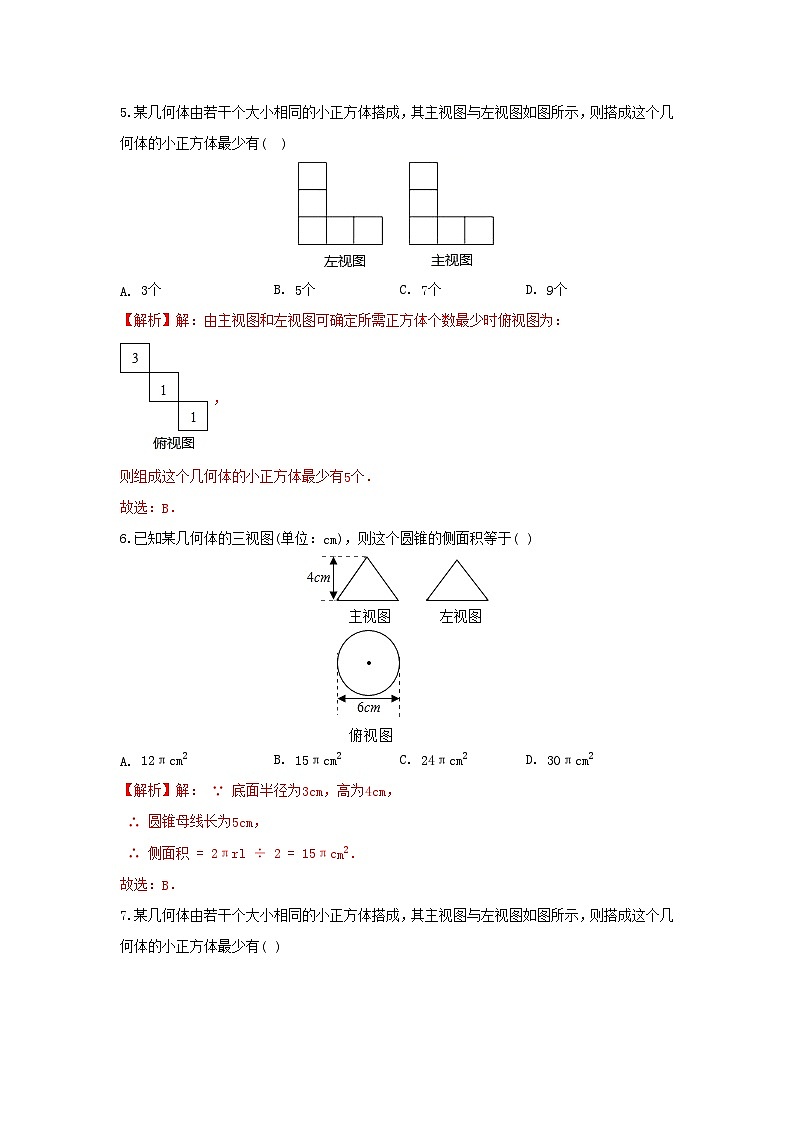
5.某几何体由若干个大小相同的小正方体搭成，其主视图与左视图如图所示，则搭成这个几何体的小正方体最少有

1. 
   个 B. 个 C. 个 D. 个

6.已知某几何体的三视图单位：，则这个圆锥的侧面积等于

1. 
    B.  C.  D.

7.某几何体由若干个大小相同的小正方体搭成，其主视图与左视图如图所示，则搭成这个几何体的小正方体最少有
 

A. 个 B. 个 C. 个 D. 个

8.如图，某剧院舞台上的照明灯P射出的光线形成“锥体”，该“锥体”截面图的“锥角”是60°.已知舞台ABCD是边长为6m的正方形，要使灯光恰好能照射到整个舞台，则照明灯P悬挂的高度是(   )

1.                                                              m B.m C.m D.m

9.用小立方块搭成的几何体，从正面看和从上面看的形状图如下，则组成这样的几何体需要的立方块个数为(   )21·

A.最多需要8块，最少需要6块 B.最多需要9块，最少需要6块

C.最多需要8块，最少需要7块 D.最多需要9块，最少需要7块

10.如图,路灯距地面8 m,身高1.6 m的小明从点A处沿所在的直线行走14 m到,点B处时,人影的长度(   )

A。变长3.5m  B.变长2.5m  C.变短3.5m  D.变短2.5m

二、填空题（共24分）

11.如图，是一个由若干个小正方体搭成的几何体的主视图与视图，设搭这样的几何体最多需要m块小立方块，最少需要n块小立方块，则m+n=_____．

12．有高度相同的一段方木和一段圆木，体积之比是1:1．在高度不变的情况下，如果将方木加工成尽可能大的圆柱，将圆木加工成尽可能大的长方体，则得到的圆柱和长方体的体积之比为____．

13. 如图是一个三棱柱的三视图，在△EFG中，EF＝6 cm，EG＝10 cm，∠EGF＝30°，则AB的长为________cm.

14.在同一时刻两根垂直于水平地面的木杆在太阳光下的影子如图所示，其中木杆AB＝2.5 m，它的影子BC＝2 m，木杆PQ的影子有一部分落在了墙上(MN)，PM＝1.6 m，MN＝1 m，则木杆PQ的长度为________．

15.一个几何体的主视图和俯视图如图所示，若这个几何体最多由m个小正方体组成，最少由n个小正方体组成，则m＋n＝________

16.如图，小芸用灯泡O照射一个矩形相框ABCD，在墙上形成影子A′B′C′D′．现测得OA＝20cm，OA′＝50cm，相框ABCD的面积为80cm2，则影子A′B′C′D′的面积为_____cm2．

三、解答题（共66分）．

17.（6分）学校食堂厨房的桌子上整齐地摆放着若干个相同规格的碟子，每一摞碟子的个数与碟子的高度的关系如下表:

（1）当桌子上放有x个碟子时，请写出碟子的高度；(用含x的式子表示)
（2）分别从三个方向上看，其三视图如图所示，厨房师傅想把它们整齐叠成一摞，求叠成一摞后的高度.2·1·

.

18.（8分）在生活中需测量一些球(如足球、篮球…)的直径,某校研究性学习小组,通过实验发现下面的测量方法:如图所示,将球放在水平的桌面上,在阳光的斜射下,得到球的影子长度为.设光线分别与球相切于点,则线段即为球的直径.若测得,请你计算球的直径.

19.（8分）一个几何体是由若干个棱长为的小正方体堆积而成的，从不同方向看到的几何体的形状图如下．
在从上面看得到的形状图中标出相应位置小正方体的个数；
这个几何体的表面积是______．

20.（10分）如图是一个几何体从三个方向看所得到的形状图．

(1)写出这个几何体的名称；

(2)画出它的一种表面展开图；

(3)若从正面看的高为4cm，从上面看三角形的边长都为3 cm，求这个几何体的侧面积．

21．（10分）)按要求完成下列问题．

(1)如图①，它是由6个同样大小的正方体摆成的几何体．将正方体①移走后，新几何体的三视图与原几何体的三视图相比，哪一个视图没有发生改变？

(2)如图②，请你借助虚线网格(甲)画出该几何体的俯视图．

(3)如图③，它是由几个小正方形组成的俯视图，小正方形上的数字表示该位置上的正方体的个数，请你借助虚线网格(乙)画出该几何体的主视图．

(4)如图④，它是由8个大小相同的正方体组成的几何体的主视图和俯视图，请你借助虚线网格(丙)画出该几何体的左视图．

22.（12分）如图所示，一幢楼房AB背后有一台阶CD，台阶每层高0.2米，且AC＝14.5米，NF＝0.2米．设太阳光线与水平地面的夹角为α，当α＝56.3°时，测得楼房在地面上的影长AE＝10米，现有一只小猫睡在台阶的NF这层上晒太阳．

(1)求楼房的高度约为多少米？

(2)过了一会儿，当α＝45°时，问小猫能否还晒到太阳？请说明理由．(参考数据：sin 56.3°≈0.83，cos 56.3°≈0.55，tan 56.3°≈1.5)

23.（12分）如图，抛物线与轴交于点，，与轴交于点．
试求，，的坐标；
将绕中点旋转，得到．
求点的坐标；
判断四边形的形状，并说明理由；
在该抛物线对称轴上是否存在点，使与相似？若存在，请直接写出所有满足条件的点的坐标；若不存在，请说明理由．