2018年天津市中考数学试卷

这是一份2018年天津市中考数学试卷，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
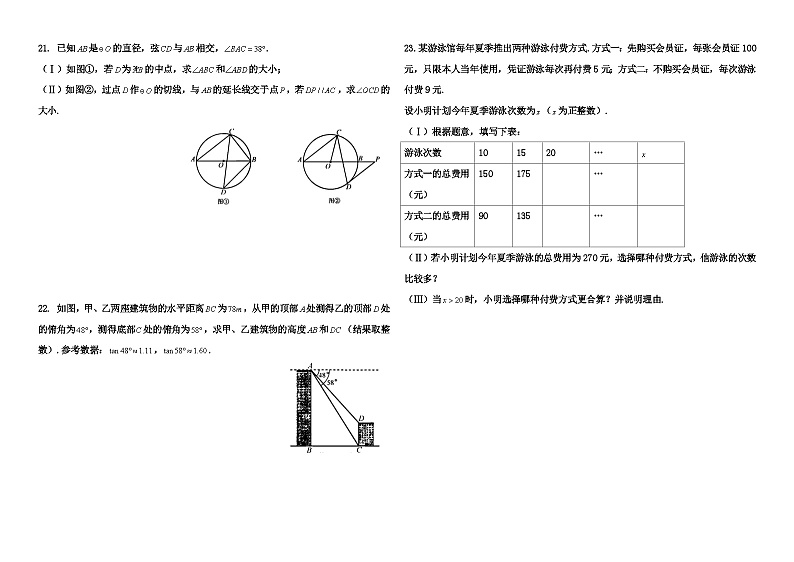
2018年天津市初中毕业生学业考试试卷  数　　学一、选择题（本大题共12小题，每小题3分，共36分）1. 计算的结果等于（  ）A．5         B．       C．9       D．2. 的值等于（  ）A．         B．       C．1       D．3. 今年“五一”假期，我市某主题公园共接待游客77800人次，将77800用科学计数法表示为（  ）A．         B．       C．        D． 4.下列图形中，可以看作是中心对称图形的是（  ）A．  B．   C.   D．5.下图是一个由5个相同的正方体组成的立体图形，它的主视图是（  ）  A．    B．    C.      D．6.估计的值在（  ）A．5和6之间       B．6和7之间     C. 7和8之间       D．8和9之间7.计算的结果为（  ）A．1         B．3       C.         D．8.方程组的解是（  ）A．         B．       C.         D．9.若点，，在反比例函数的图像上，则，，的大小关系是（  ）A．         B．       C.         D．10.如图，将一个三角形纸片沿过点的直线折叠，使点落在边上的点处，折痕为，则下列结论一定正确的是（  ）A．         B．       C.     D．                             11.如图，在正方形中，，分别为，的中点，为对角线上的一个动点，则下列线段的长等于最小值的是（  ）A．         B．       C.         D．12.已知抛物线（，，为常数，）经过点，，其对称轴在轴右侧，有下列结论：①抛物线经过点；②方程有两个不相等的实数根；③.其中，正确结论的个数为（  ）A．0         B．1       C.2         D．3二、填空题（本大题共6小题，每小题3分，共18分）13.计算的结果等于          ．14.计算的结果等于          ．15.不透明袋子中装有11个球，其中有6个红球，3个黄球，2个绿球，这些球除颜色外无其他差别.从袋子中随机取出1个球，则它是红球的概率是          ．16.将直线向上平移2个单位长度，平移后直线的解析式为          ．17.如图，在边长为4的等边中，，分别为，的中点，于点，为的中点，连接，则的长为          ．                           18.如图，在每个小正方形的边长为1的网格中，的顶点，，均在格点上.（1）的大小为          （度）；（2）在如图所示的网格中，是边上任意一点.为中心，取旋转角等于，把点逆时针旋转，点的对应点为.当最短时，请用无刻度的直尺，画出点，并简要说明点的位置是如何找到的（不要求证明）          ． 三、解答题 （本大题共7小题，共66分.解答应写出文字说明、演算步骤或推理过程.）  19. 解不等式组请结合题意填空，完成本题的解答.（Ⅰ）解不等式（1），得          ．（Ⅱ）解不等式（2），得          ．（Ⅲ）把不等式（1）和（2）的解集在数轴上表示出来：（Ⅳ）原不等式组的解集为           ． 20. 某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡，根据它们的质量（单位：），绘制出如下的统计图①和图②.请根据相关信息，解答下列问题：（Ⅰ）图①中的值为          ；（Ⅱ）求统计的这组数据的平均数、众数和中位数；（Ⅲ） 根据样本数据，估计这2500只鸡中，质量为的约有多少只？             21. 已知是的直径，弦与相交，.（Ⅰ）如图①，若为的中点，求和的大小；（Ⅱ）如图②，过点作的切线，与的延长线交于点，若，求的大小.     22. 如图，甲、乙两座建筑物的水平距离为，从甲的顶部处测得乙的顶部处的俯角为，测得底部处的俯角为，求甲、乙建筑物的高度和（结果取整数）.参考数据：，.   23.某游泳馆每年夏季推出两种游泳付费方式.方式一：先购买会员证，每张会员证100元，只限本人当年使用，凭证游泳每次再付费5元；方式二：不购买会员证，每次游泳付费9元.设小明计划今年夏季游泳次数为（为正整数）.（Ⅰ）根据题意，填写下表：游泳次数101520…方式一的总费用（元）150175 … 方式二的总费用（元）90135 … （Ⅱ）若小明计划今年夏季游泳的总费用为270元，选择哪种付费方式，他游泳的次数比较多？（Ⅲ）当时，小明选择哪种付费方式更合算？并说明理由.          24.在平面直角坐标系中，四边形是矩形，点，点，点.以点为中心，顺时针旋转矩形，得到矩形，点，，的对应点分别为，，.（Ⅰ）如图①，当点落在边上时，求点的坐标；（Ⅱ）如图②，当点落在线段上时，与交于点.①   求证；②   求点的坐标.（Ⅲ）记为矩形对角线的交点，为的面积，求的取值范围（直接写出结果即可）.           25.在平面直角坐标系中，点，点.已知抛物线（是常数），定点为.（Ⅰ）当抛物线经过点时，求定点的坐标；（Ⅱ）若点在轴下方，当时，求抛物线的解析式；（Ⅲ） 无论取何值，该抛物线都经过定点.当时，求抛物线的解析式.                  2018年参考答案（1）C（2）B（3）B（4）A（5）A（6）D（7）C（8）A（9）B（10）D（11）D（12）C二、(13) 2x7 (14) 3(15) 6/11(16) y=x+2 (17) （18）（Ⅰ）90；（Ⅱ）如图，取格点D，E，连接DE交AB于点T；取格点M，N，连接MN交BC延长线于点G；取格点F，连接FG交TC于点P’，则点P’即为所求。（19）（1）；（2）；（3）（4）（20）解：（1）m%=100%-32%-22%-10%-8%=28%，故m=28.（2）观察条形统计图，∵x=；∴这组数据的平均数是1.52.∵在这组数据中，1.8出现了16次，出现的次数最多，∴这组数据的众数为1.8.∵将这组数据按从小到大的顺序排列，其中处于中间的两个数都是1.5，∴这组数据的中位数为1.5.（3）∵在所取的样本中，质量为2.0kg的数量占8%，∴由样本数据，估计这2500只鸡中，质量为2.0kg的数量约占8%.则有：2500×8%=200.∴这2500只鸡中，质量为2.0kg的约有200只.（21）解：（I）∵AB是⊙O直径∴∠ACB=90°∴∠BAC+∠ABC=90°又∵∠BAC=38°∴∠ABC=90°-38°=52°∵弧AD=弧BD∴∠ACD=∠BCD=∠ACB=45°∴∠ABD=∠ACD=45°（Ⅱ）如图，连接OD∵DP切⊙O与点D∴OD⊥DP，即∠ODP=90°∵DP∥AC，∠BAC=38°∴∠P=∠BAC=38°∵∠AOD是△ODP的外角∴∠AOD=∠ODP+∠P=128°∴∠ACD=∠AOD=64°∵OA=OC∴∠ACO =∠A=38°∴∠OCD=∠ACD-∠ACO=64°-38°=26°(22)解：如图，过点D作DE⊥AB，垂足为E则∠AED=∠BED=90°由题意可知，BC=78，∠ADE=48°，∠ACB=58°，∠ABC=90°，∠DCB=90°可得四边形BCDE为矩形∴ED=BC=78，DC=EB在Rt△ABC中，tan∠ACB= ∴AB =BC·tan58°≈78×1.60≈125 在Rt△AED中，tan∠ADE= ∴AE=ED·tan48°∴EB=AB-AE=BC·ED·tan48°≈78×1.60-78×1.11≈38∴DC=EB≈38答：甲建筑物的高度AB约为125m,乙建筑物的高度DC约为38m.(23)解：（Ⅰ）200，,180，.   （Ⅱ）方式一：，解得         方式二：，解得         ,         小明选择方式一游泳次数比较多.   （Ⅲ）设方式一和方式二的总费用的差为元.         则，即         当时，即，得         当时，小明选择这两种方式一样合算.         ,         随的增大而减小.         当时，有，小明选择方式二更合算；           当时，有，小明选择方式一更合算；(24) 解：（I）        ∵点A（5，0），点B（0，3），∴OA=5，OB=3,∵四边形AOBC是矩形，∴AC=BO=3，BC=OA=5，∠OBC=∠C=90°.∵矩形ADEF是由矩形AOBC旋转得到的，∴AD=AO=5.在Rt△ADC中，有AD²=AC²+DC²，∴DC===4.∴BD=BC-DC=1.∴点D的坐标为（1,3）.（II）    ①由四边形ADEF是矩形，得∠ADE=90°.又点D在线段BE上，得∠ADB=90°.由（Ⅰ）知，AD=AO，又AB=AB，∠AOB=90°，∴Rt△ADB≌Rt△AOB；②由△ADB≌△AOB得∠BAD=∠BAO.又在矩形AOBC中，OA∥BC,∴∠CBA=∠OAB.∴∠BAD=∠CBA.∴BH=AH.设BH=t，则AH=t，HC=BC-BH=5-t.在Rt△AHC中，有AH²=AC²+HC²,∴t²=3²+（5-t）².解得t=.∴BH=.∴点H的坐标为（，3）（III） ≤ S ≤ .当D点落在线段AB上时，△KDE的面积最小，为；当D点在BA的延长线上时，△KDE的面积最大，为 .        (25)解：（1）∵抛物线经过点A（1，0），∴，解得.∴抛物线的解析式为.∵，∴顶点P的坐标为（）. （2）抛物线的顶点P的坐标为.由点A（1，0）在x轴正半轴上，点P在轴下方，，知点P在第四象限.  过点P作PQ轴于点Q，则  可知PQ=OQ，即，解得.  当时，点P不在第四象限，舍去.∴∴抛物线解析式为. （3）由可知，  当时，无论取何值，都等于4.  得点H的坐标为（2，4）.  过点A作AD，交射线HP于点D，分别过点D，H作x轴的垂线，垂足分别为E，G则  ∵∴∴∵，∴.∴∴.可得点D的坐标为（-3，1）或（5，-1）.①点D的坐标为（-3，1）时，可得直线DH的解析式为.∵点P 在直线上，∴= .解得当时，点P与点H重合，不符合题意，∴=②当点D的坐标为（5，-1）时，可得直线DH的解析式为.∵点P 在直线上，∴= -.解得（舍），∴综上或故抛物线解析式为或.