人教版八年级数学上册第十二章过关训练课件

这是一份人教版八年级数学上册第十二章过关训练课件，共35页。

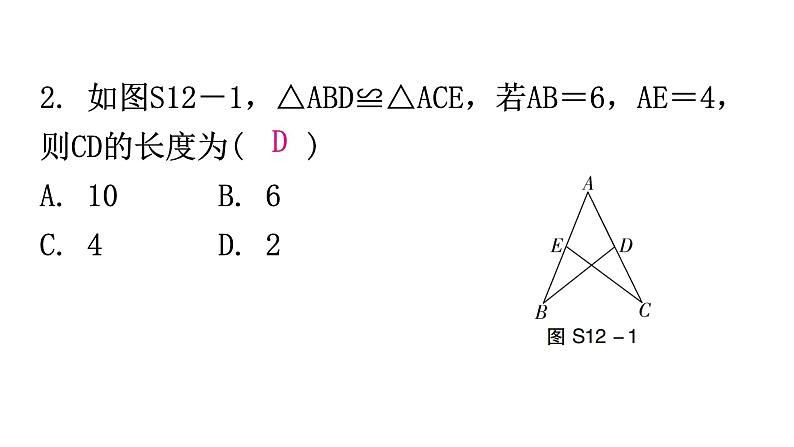
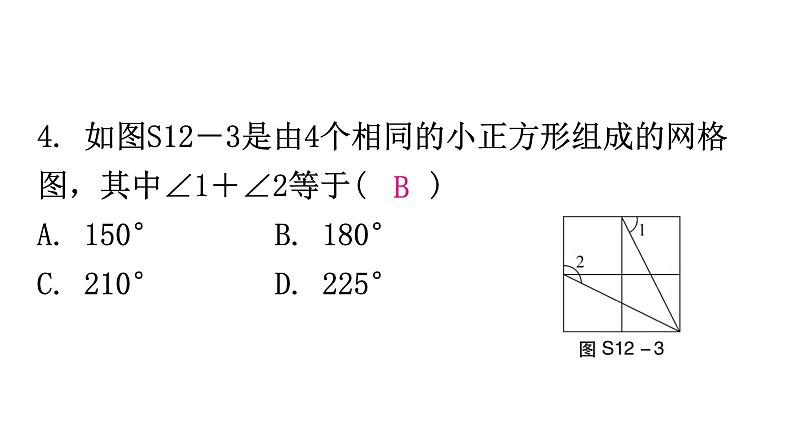
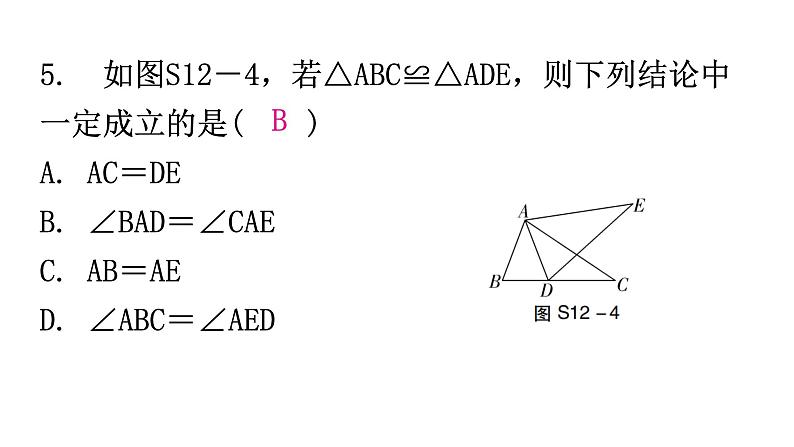
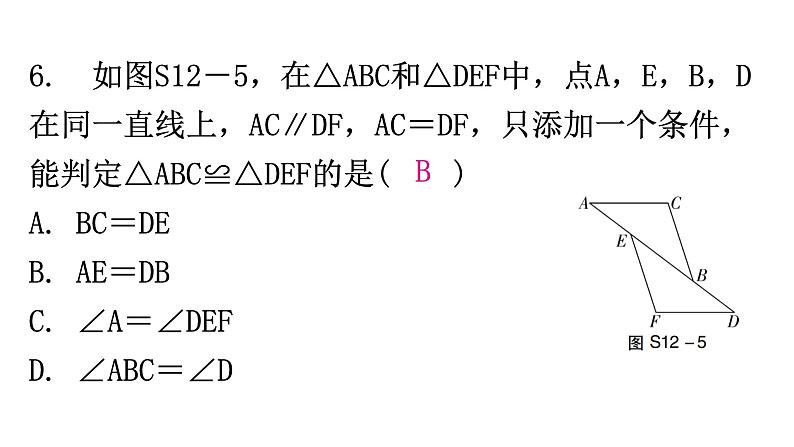
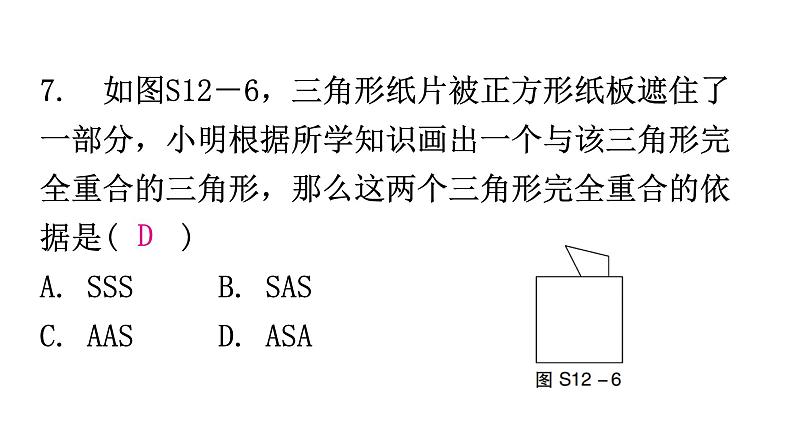
第十二章过关训练一、选择题(本大题共10小题，每题3分，共30分)1. 下列各组的两个图形属于全等图形的是( ) D2. 如图S12－1，△ABD≌△ACE，若AB＝6，AE＝4，则CD的长度为( )A. 10 B. 6 C. 4 D. 2D3. 如图S12－2，△ABC≌△EBD，若∠E＝50°，∠D＝62°，则∠ABC的度数是( )A. 68° B. 62°C. 60° D. 50°A 4. 如图S12－3是由4个相同的小正方形组成的网格图，其中∠1＋∠2等于( )A. 150° B. 180°C. 210° D. 225°B5. 如图S12－4，若△ABC≌△ADE，则下列结论中一定成立的是( )A. AC＝DEB. ∠BAD＝∠CAEC. AB＝AED. ∠ABC＝∠AEDB6. 如图S12－5，在△ABC和△DEF中，点A，E，B，D在同一直线上，AC∥DF，AC＝DF，只添加一个条件，能判定△ABC≌△DEF的是( )A. BC＝DEB. AE＝DBC. ∠A＝∠DEFD. ∠ABC＝∠DB7. 如图S12－6，三角形纸片被正方形纸板遮住了一部分，小明根据所学知识画出一个与该三角形完全重合的三角形，那么这两个三角形完全重合的依据是( )A. SSS B. SASC. AAS D. ASAD8. 如图S12－7，在四边形ABCD中，∠A＝90°，AD＝3，BC＝5，对角线BD平分∠ABC，则△BCD的面积为( )A. 8 B. 7.5C. 15 D. 无法确定B9. 如图S12－8，在平面直角坐标系中，A(2，0)，B(0，4)，若以B，O，C为顶点的三角形与△ABO全等，则点C的坐标不能为( )A. (0，－4)B. (－2，0)C. (2，4)D. (－2，4)A10. 两组邻边分别相等的四边形叫做“筝形”，如图S12－9，四边形ABCD是一个筝形，其中AD＝CD，AB＝CB，在探究筝形的性质时，得到如下结论：①△ABD≌△CBD；②AC⊥BD；③四边形ABCD的面积为2AC·BD，其中正确的结论有( )A. 0个 B. 1个C. 2个 D. 3个C二、填空题(本大题共5小题，每题3分，共15分)11. 如图S12－10，如果图中的两个三角形全等，根据图中所标数据，可以推理得到角α＝__________. 42°12. 如图S12－11，已知∠DCE＝90°，∠DAC＝90°，BE⊥AC于点B，且DC＝EC.若BE＝7，AB＝3，则AD的长为________. 413. 如图S12－12，为了测量A，B两点之间的距离，在地面上找到一点C，连接BC，AC，使∠ACB＝90°，然后在BC的延长线上确定点D，使CD＝BC，那么只要测量出AD的长度就得到A，B两点之间的距离，其中△ABC≌△ADC的依据是__________．SAS14. 如图S12－13，小明与小红玩跷跷板游戏，如果跷跷板的支点O(即跷跷板的中点)与地面的距离是50 cm，当小红从水平位置CD下降30 cm时，这时小明离地面的高度是________cm.8015. 如图S12－14，在长方形ABCD中，AB＝4，AD＝6，延长BC到点E，使CE＝2，连接DE，动点P从点B出发，以每秒2个单位长度的速度沿BC→CD→DA向终点A运动.设点P的运动时间为t s，当t的值为________时，△ABP和△DCE全等.1或7三、解答题(一)(本大题共3小题，每题8分，共24分)16. 如图S12－15，△ABC是等腰三角形，点D，E分别在腰AC，AB上，且BE＝CD，连接BD，CE.求证：BD＝CE.17. 如图S12－16，在△ADF和△BCE中，AF＝BE，AC＝BD，∠A＝∠B，∠B＝32°，∠F＝28°，BC＝5 cm，CD＝1 cm. 求：(1)∠1的度数；(2)AC的长. 解：(1)∵AC＝BD,∴AC－CD＝BD－CD,即AD＝BC.又∵AF＝BE，∠A＝∠B,∴△ADF≌△BCE(SAS).∴∠E＝∠F＝28°.∴∠1＝∠B＋∠E＝32°＋28°＝60°.(2)由（1）知，AD＝BC＝5 cm，∵CD＝1 cm，∴AC＝AD＋CD＝6(cm). 18. 如图S12－17，在△ABC中，∠B＝30°，∠A＝130°.(1)尺规作图：作∠A的平分线，交BC于点D；(不写作法，保留作图痕迹)(2)求∠ADC的度数. 四、解答题(二)(本大题共3小题，每题9分，共27分)19. 如图S12－18，AD∥BC，∠A＝90°，以点B为圆心，BC长为半径画弧，与射线AD相交于点E，连接BE，过点C作CF⊥BE，垂足为F. (1)线段BF＝__________；(填写图中现有的一条线段)(2)证明(1)中的结论. AE20. 如图S12－19，AB＝AC，∠BAC＝90°，BD⊥AE于点D，CE⊥AE于点E，且BD＞CE. 求证：BD＝EC＋ED. 21. 如图S12－20，两根旗杆相距11 m，小华从点B沿BA走向点A，一定时间后到达点M，此时他仰望旗杆的顶点C和D，两次视线的夹角为90°，且CM＝DM.已知旗杆AC的高度为5 m，小华的运动速度为1.5 m/s.(1)小华还需运动多长时间才能到达点A？(2)求旗杆DB的长.(2)由(1)知，△ACM≌△BMD，AM＝6 m,∴DB＝AM＝6 m.答：旗杆DB的长为6 m.五、解答题(三)(本大题共2小题，每题12分，共24分)22. 如图S12－21，在四边形ABCD中，E为BC边的中点. 若AE平分∠BAD，∠AED＝90°，F为AD上一点，且AF＝AB. 求证：(1)△ABE≌△AFE；(2)AD＝AB＋CD.23. 在△ABC中，AB＝AC，D是直线BC上一点，以AD为一边在AD的右侧作△ADE，使AE＝AD，∠DAE＝∠BAC，连接CE，设∠BAC＝α，∠DCE＝β.(1)如图S12－22①，当点D在线段BC上移动时，试证明：△ABD≌△ACE；(2)如图S12－22②，当点D在线段BC的延长线上移动时，探索角α与β之间的数量关系并证明；(3)当点D在线段BC的反向延长线上移动时，请在备用图上根据题意画出图形，并猜想角α与β之间的数量关系是__________，线段BC，DC，CE之间的数量关系是__________________.α＝βBC＋CE＝DC(3)图略.