资料中包含下列文件,点击文件名可预览资料内容





还剩8页未读,
继续阅读
所属成套资源:七年级数学上册尖子生选拔卷(人教版)
成套系列资料,整套一键下载
第四章 几何图形初步(选拔卷)-七年级数学上册尖子生选拔卷(人教版)
展开
这是一份第四章 几何图形初步(选拔卷)-七年级数学上册尖子生选拔卷(人教版),文件包含第四章几何图形初步选拔卷-七年级数学上册尖子生选拔卷人教版原卷版doc、第四章几何图形初步选拔卷-七年级数学上册尖子生选拔卷人教版解析版doc、第四章几何图形初步选拔卷-七年级数学上册尖子生选拔卷人教版答题纸docx、第四章几何图形初步选拔卷-七年级数学上册尖子生选拔卷人教版考试版doc等4份试卷配套教学资源,其中试卷共48页, 欢迎下载使用。
第四章 几何图形初步(人教版)
选拔卷
(考试时间:90分钟 试卷满分:120分)
一、选择题:本题共10个小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
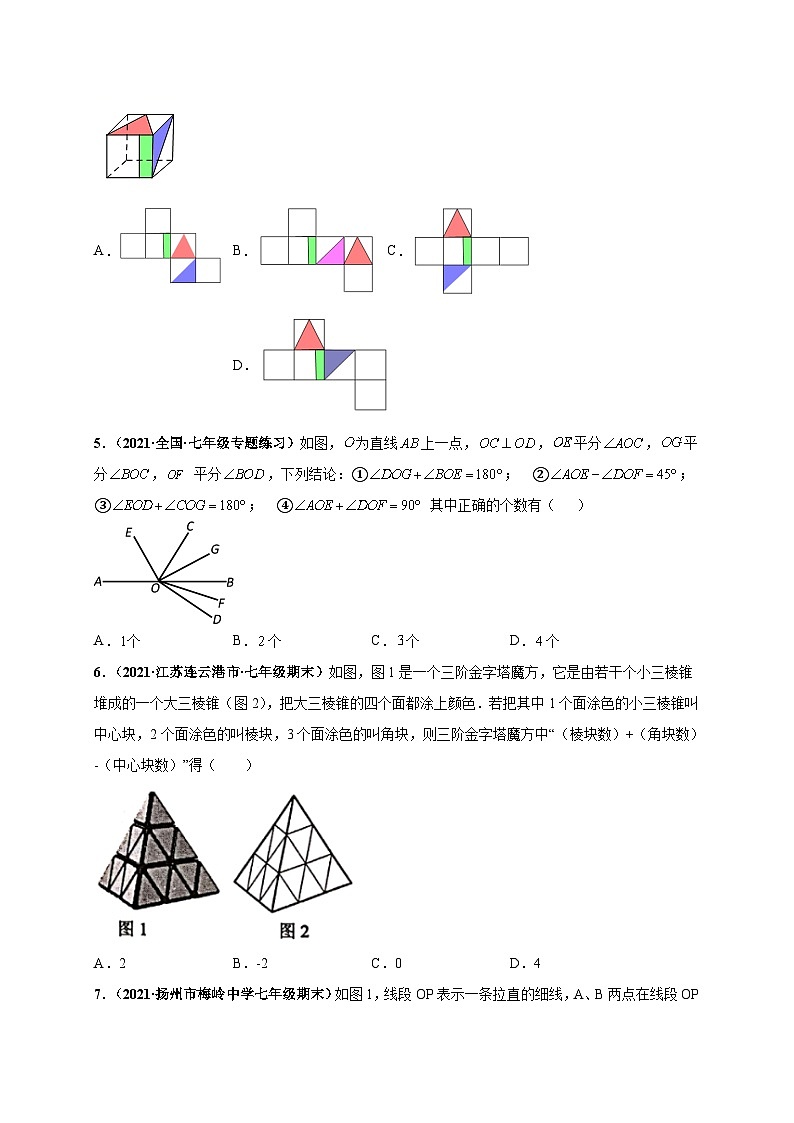
1.(2021·北京二中七年级期末)有5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形折叠后能成为一个封闭的正方体盒子,你不能选择图中A,B,C,D中的( )位置拼接正方形.
A.A B.B C.C D.D
【答案】A
【分析】结合正方体的平面展开图的特征,只要折叠后能围成正方体即可.
【详解】解:如图所示:
根据立方体的展开图可知,不能选择图中A的位置接正方形.故选:A.
【点睛】此题主要考查了应用与设计作图.正方体的平面展开图共有11种,应灵活掌握,不能死记硬背.
2.(2021·浙江省义乌市望道中学七年级月考)如图,已知的顶点在直线上,平分,平分,则的度数是( )
A. B. C. D.
【答案】D
【分析】运用角平分线的定义算出∠FOE=2∠COF,再由∠COE为直角,可求出∠COF的度数,再求出∠AOF的度数,最后可求得∠BOE的度数.
【详解】解:∵平分∴∠AOF=∠FOE
∵平分∴∠AOF=2∠COF∴∠FOE=2∠COF
又∠COE是直角∴∴∠AOF=∠FOE=60°
∴故选:D.
【点睛】此题考查角平分线的定义和角的有关运算.发现组成RT∠COE的两个角:∠FOE=2∠COF是解决问题的关键.
3.(2020·广东省初一月考)如图,是一个带有方形空洞和圆形空洞的儿童玩具,如果用下列几何体作为塞子,那么既可以堵住方形空洞,又可以堵住圆形空洞的几何体是( )
A. B. C. D.
【答案】B
【解析】圆柱从上边看是一个圆,从正面看是一个正方形,既可以堵住方形空洞,又可以堵住圆形空洞,故选B.
考点:简单几何体的三视图.
4.(2021·山西吕梁市·七年级期末)有一种正方体如图所示,下列图形是该正方体的展开图的是( )
A. B. C. D.
【答案】D
【分析】根据题意,三个图形有一个公共顶点,其中绿色长方形与等腰直角三角形有一条公共边,据此逐项分析解题.
【详解】解:A.折叠后,三个图形没有公共顶点,故A不符合题意;
B.折叠后,长方形与普通三角形是相对面,故B不符合题意;C.折叠后,两个三角形是相对面,故C不符合题意;D.折叠后,三个图形有一个公共顶点,其中绿色长方形与等腰直角三角形有一条公共边,故D符合题意,故选:D.
【点睛】本题考查正方体的表面展开图,是重要考点,难度较易,掌握相关知识是解题关键.
5.(2021·全国·七年级专题练习)如图,为直线上一点,,平分,平分, 平分,下列结论:①; ②;
③; ④ 其中正确的个数有( )
A.个 B.个 C.个 D.个
【答案】C
【分析】根据余角和补角的定义以及角平分线的定义,计算出各选项的结果判断即可.
【详解】解:∵平分,平分,∴,,
∴,
∵,∴,∴,∴,
∵,∴,故①正确;
∵,∵平分,平分,
∴,∴,故②正确;
∵,∴,
∴,故③正确;
∵不能证明,故④错误;∴正确的选项有3个;故选:C.
【点睛】本题考查了同角的补角相等,同角的余角相等,角的平分线,以及角的运算,解题的关键是熟练掌握角的平分线性质,余角和补角的定义,从而进行计算.
6.(2021·江苏连云港市·七年级期末)如图,图1是一个三阶金字塔魔方,它是由若干个小三棱锥堆成的一个大三棱锥(图2),把大三棱锥的四个面都涂上颜色.若把其中1个面涂色的小三棱锥叫中心块,2个面涂色的叫棱块,3个面涂色的叫角块,则三阶金字塔魔方中“(棱块数)+(角块数)-(中心块数)”得( )
A.2 B.-2 C.0 D.4
【答案】B
【分析】根据三阶魔方的特征,分别求出棱块数、角块数、中心块数,再计算即可.
【详解】解:如图所示:
∵3个面涂色的小三棱锥为四个顶点处的三棱锥,共4个,∴角块有4个;
∵2个面涂色的小三棱锥为每两个面的连接处,共6个,∴棱块有6个;
∵1个面涂色的小三棱锥为每个面上不与其他面连接的部分,即图中的阴影部分的3个,
∴中心块有:(个);∴(棱块数)+(角块数)(中心块数)=;选:B.
【点睛】本题考查了三阶魔方的特征,认识立体图形,图形的规律;解题的关键是正确的认识三阶魔方的特征,从而进行解题.
7.(2021·扬州市梅岭中学七年级期末)如图1,线段OP表示一条拉直的细线,A、B两点在线段OP上,且OA:AP=1:2,OB:BP=2:7.若先固定A点,将OA折向AP,使得OA重叠在AP上;如图2,再从图2的B点及与B点重叠处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比是( )
A.1:1:2 B.2:2:5 C.2:3:4 D.2:3:5
【答案】B
【分析】根据题意设OB的长度为2a,则BP的长度为7a,OP的长度为9a,从而根据比值可以得到图一中各线段的长,根据题意可以求出折叠后,再剪开各线段的长度,从而可以求得三段细线由小到大的长度比,本题得以解决.
【详解】解:设OB的长度为2a,则BP的长度为7a,OP的长度为9a,
∵OA:AP=1:2,∴OA=3a,AP=6a,
又∵先固定A点,将OA折向AP,使得OA重叠在AP上,如图2,再从图2 的B点及与B点重迭处一起剪开,使得细线分成三段,
∴这三段从小到大的长度分别是:2a、2a、5a,
∴此三段细线由小到大的长度比为:2a:2a:5a=2:2:5,故选:B.
【点睛】本题考查比较线段的长短,解题的关键是理解题意,求出各线段的长度.
8.(2021·四川成都市·成都实外)如图,将长方形纸片ABCD的∠C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若∠BFE=3∠BFH,∠BFH=20°,则∠GFH的度数是( )
A.85° B.90° C.95° D.100°
【答案】D
【分析】根据折叠求出∠CFG=∠EFG=∠CFE,根据∠BFE=3∠BFH,∠BFH=20°,即可求出∠GFH=∠GFE+∠HFE的度数.
【详解】解:∵将长方形纸片ABCD的角C沿着GF折叠(点F在BC上,不与B,使点C落在长方形内部点E处,∴∠CFG=∠EFG=∠CFE,
∵∠BFE=3∠BFH,∠BFH=20°,∴∠BFE=60°,∴∠CFE=120°,∴∠GFE=60°,
∵∠EFH=∠EFB﹣∠BFH,∴∠EFH==40°,∴∠GFH=∠GFE+∠EFH=60°+40°=100°.选:D.
【点睛】本题考查了角的计算,折叠的性质,角度的倍数关系,主要考查学生的推理和计算能力.
9.(2021·河南省淮滨县第一中学七年级期末)如图,直线相交于点,平分,射线将分成了角度数之比为的两个角,则的大小为( )
A. B. C.或 D.或
【答案】C
【分析】设∠DOE=x°,∠BOD=2x°或x°,表示出其他角,根据平角列方程即可.
【详解】解:设∠DOE=x°,射线将分成了角度数之比为的两个角,
当∠DOE:∠BOD=2:1时,∠BOD=x°,=x°,
∵平分,∴=x°,
∵∠COD=180°,∴x+x+90+ x=180,解得,x=45;∠COF=2∠AOC=45°;
当∠BOD: ∠DOE =2:1时,∠BOD=2x°,=2x°,同理, =2x°,
2x+2x+90+ x=180,解得:x=18,∠COF=2∠AOC=72°;故选:C.
【点睛】本题考查了角的运算、角的度量和角平分线,解题关键是根据角度比设未知数,表示出其他角,然后根据平角列方程,注意:分类讨论.
10.(2021·全国·九年级专题练习)如图,点M在线段AN的延长线上,且线段MN=20,第一次操作:分别取线段AM和AN的中点;第二次操作:分别取线段和的中点;第三次操作:分别取线段和的中点;……连续这样操作10次,则每次的两个中点所形成的所有线段之和( )
A. B. C. D.
【答案】A
【分析】根据,分别为的中点,求出的长度,再由的长度求出的长度,找到的规律即可求出的值.
【详解】解:∵,分别为的中点,
∴,
∵分别为的中点,
∴,根据规律得到,
∴,故选A.
【点睛】本题是对线段规律性问题的考查,准确根据题意找出规律是解决本题的关键,相对较难.
二、填空题:本题共8个小题,每题3分,共24分。
11.(2021·河北保定师范附属学校九年级期末)如图2是图1中长方体的三视图,若用S表示面积,,,则
【答案】20
【分析】由主视图和左视图的宽为x,结合两者的面积得出俯视图的长和宽,从而得出答案.
【详解】解:∵S主=5x,S左=4x,且主视图和左视图的宽为x,
∴俯视图的长为5,宽为4,则俯视图的面积S俯=5×4=20.
【点睛】本题主要考查由三视图判断几何体,解题的关键是根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,以及几何体的长、宽、高.
12.(2021·浙江浙江省·)已知三点在同一条直线上,且线段,点分别是线段的中点点F是线段的中点,则_______.
【答案】或
【分析】根据中点定义求出BD、BE的长度,然后分①点C在AB的延长线上时,求出DE的长度,再根据中点定义求出EF的长,然后根据BF=BE-EF代入数据进行计算即可得解;②点C在AB的反向延长线上时,求出DE的长度,再根据中点定义求出EF的长,然后根据BF=BE-EF代入数据进行计算即可得解.
【详解】解:、分别是线段、的中点,,,
,,
①如图1,点在的延长线上时,,
点是线段的中点,,此时,;
②如图2,点在的反向延长线上时,,
点是线段的中点,,此时,,
综上所述,或.故答案为:或.
【点睛】本题考查两点间的距离,线段中点的定义,难点在于要分情况讨论,作出图形更形象直观.
13.(2021·山西运城市·七年级期末)一个几何体由一些大小相同的小正方体搭成,从正面和左面看到的这个几何体的形状如图所示,则搭成该几何体的小正方体的个数最少是___________.
【答案】4
【分析】由主视图和左视图确定俯视图的形状,再判断最少的正方体的个数.
【详解】解:由题中所给出的主视图知物体共3列,且都是最高两层;由左视图知共3行,
所以小正方体的个数最少的几何体为:
第一列第一行1个小正方体,第二列第二行2个小正方体,第三列第三行1个小正方体,其余位置没有小正方体.即组成这个几何体的小正方体的个数最少为:1+2+1=4个.故答案为:4.
【点睛】本题考查了学生对三视图的掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就更容易得到答案.
14.(2020·四川省初一期中)瑞士著名数学家欧拉发现:简单多面体的顶点数V、面数F及棱数E之间满足一种有趣的关系:V+F﹣E=2,这个关系式被称为欧拉公式.比如:正二十面体(如右图),是由20个等边三角形所组成的正多面体,已知每个顶点处有5条棱,则可以通过欧拉公式算出正二十面体的顶点为_____个.那么一个多面体的每个面都是五边形,每个顶点引出的棱都有3条,它是一个_____面体.
【答案】12. 12.
【分析】①设出正二十面体的顶点为n个,则棱有条.利用欧拉公式构建方程即可解决问题.②设顶点数V、棱数E、面数F、每个点都属于三个面,每条边都属于两个面,利用欧拉公式构建方程即可解决问题.
【解析】解:①设出正二十面体的顶点为n个,则棱有条.
由题意F=20,∴n+10﹣=2,解得n=12.
②设顶点数V,棱数E,面数F,每个点属于三个面,每条边属于两个面
由每个面都是五边形,则就有E=,V=
由欧拉公式:F+V﹣E=2,代入:F+﹣=2.化简整理:F=12 所以:E=30,V=20
即多面体是12面体.棱数是30,面数是12,故答案为12,12.
【点睛】本题考查欧拉公式的应用,解题的关键是弄清题意、利用等量关系列出方程是解答本题的关键.
15.(2021·全国·七年级专题练习)如图,点O是钟面的中心,射线正好落在3:00时针的位置.当时钟从2:00走到3:00,则经过___________分钟,时针,分针,与所在的三条射线中,其中一条射线是另外两条射线所夹角的角平分线.
【答案】6或
【分析】分两种情况讨论:当时针为角平分线和OC为角平分线进行计算即可.
【详解】设时针为OB,分针为OA. 当时针为OB为角平分线时,如图1所示:
设经过x分钟,OB为角平分线,则∠AOB=60゜-6x゜+,∠BOC=30゜-,依题意得:60-6x+=30-解得x=6;
当时针为OC为角平分线时,如图2所示:
设经过x分钟,OC为角平分线,则∠AOC=6x゜-90゜,∠BOC=30゜-,
依题意得:6x-90=30-解得x=;
综合上述可得:经过6分钟或分钟时,时针,分针,与所在的三条射线中,其中一条射线是另外两条射线所夹角的角平分线.
故答案为:6或.
【点睛】考查了一元一次方程的应用和角平分线的性质,解题关键是分两种情况讨论:当时针为角平分线和OC为角平分线和利用方程求得其角度.
16.(2020·辽宁皇姑·七年级期末)如图,在平面内,点是直线上一点,,射线不动,射线,同时开始绕点顺时针转动,射线首次回到起始位置时两线同时停止转动,射线,的转动速度分别为每秒和每秒.若转动秒时,射线,,中的一条是另外两条组成角的角平分线,则______秒.
【答案】4或5
【分析】根据已知条件可知,在第t秒时,射线OA转过的角度为40°t,射线OB转过的角度为20°t,然后按照OA、OB、OC三条射线构成相等的角分三种情况讨论:①当OA平分∠BOC;②当OC平分∠AOB;③当OB平分∠AOC,分别列方程即可求出t的值.
【详解】解:根据题意,在第t秒时,射线OA转过的角度为40°t,射线OB转过的角度为20°t,
①当OA,OB转到OA′,OB′的位置时,如图①所示,∠A′OC=∠A′OB′,
∵∠A′OC=180°-40°t,∠A′OB′=∠AOA′-∠AOB-∠BOB′=40°t-60°-20°t=20°t-60°,
∴180°-40°t =20°t-60°,即t=4;
②当OA,OB转到OA′,OB′的位置时,如图②所示,∠A′OC=∠B′OC,
∵∠A′OC=40°t-180°,∠B′OC=180°-∠AOB-∠BOB′=180°-60°-20°t=120°-20°t,
∴40°t-180°=120°-20°t,即t=5;
③当OA,OB转到OA′,OB′的位置时,如图③,∠B′OC=∠A′OB′,
∵∠B′OC=20°t-120°,∠A′OB′=∠A′OC=(180°-∠AOA′)=[180°-(360°-40°t)]=20°t-90°,
∴20°t-120°=20°t-90°,此时方程不成立.
综上所述:t的值为4或5.故答案:4或5.
【点睛】题主要考查角的和、差关系,难点是找出变化过程中的不变量,需要结合图形来计算,在计算分析的过程中注意动手操作,在旋转的过程中得到不变的量.
17.(2021·沙坪坝区·重庆南开中学七年级月考)如图,数轴上有两点,点C从原点O出发,以每秒的速度在线段上运动,点D从点B出发,以每秒的速度在线段上运动.在运动过程中满足,若点M为直线上一点,且,则的值为_______.
【答案】1或
【分析】设点A在数轴上表示的数为a,点B在数轴上表示的数为b,设运动的时间为t秒,由OD=4AC得a与b的关系,再根据点M在直线AB的不同的位置分4种情况进行解答,①若点M在点B的右侧时,②若点M在线段BO上时,③若点M在线段OA上时,④若点M在点A的左侧时,分别表示出AM、BM、OM,由AM-BM=OM得到t、a、b之间的关系,再计算的值即可.
【详解】设运动的时间为t秒,点M表示的数为m
则OC=t,BD=4t,即点C在数轴上表示的数为-t,点D在数轴上表示的数为b-4t,∴AC=-t-a,OD=b-4t,
由OD=4AC得,b-4t=4(-t-a),即:b=-4a,
①若点M在点B的右侧时,如图1所示:
由AM-BM=OM得,m-a-(m-b)=m,即:m=b-a;∴
②若点M在线段BO上时,如图2所示:
由AM-BM=OM得,m-a-(b-m)=m,即:m=a+b;∴
③若点M在线段OA上时,如图3所示:
由AM-BM=OM得,m-a-(b-m)=-m,即:
∵此时m<0,a<0,∴此种情况不符合题意舍去;
④若点M在点A的左侧时,如图4所示:
由AM-BM=OM得,a-m-(b-m)=-m,即:m=b-a=-5a;而m<0,b-a>0,因此,不符合题意舍去,
综上所述,的值为1或.
【点睛】考查数轴表示数的意义,掌握数轴上两点之间距离的计算方法是正确解答的关键,分类讨论和整体代入在解题中起到至关重要的作用.
18.(2021·重庆八中七年级期末)如图,直线AB⊥OC于点O,∠AOP=40°,三角形EOF其中一个顶点与点O重合,∠EOF=100°,OE平分∠AOP,现将三角形EOF以每秒6°的速度绕点O逆时针旋转至三角形E′OF′,同时直线PQ也以每秒9°的速度绕点O顺时针旋转至P′Q′,设运动时间为m秒(0≤m≤20),当直线P′Q′平分∠E′OF′时,则∠COP′=___.
【答案】或
【分析】由题意,分两种情况讨论,当平分时,当平分时作出图形,分别画出对应图,对比开始时刻的角度,通过角度的加减计算即可.
【详解】平分,,
以每秒的速度绕点O逆时针旋转,以每秒的速度点O顺时针旋转,
①如图1中,当平分时,
解得
,
②如图2,当平分时,
解得
故答案为:或
【点睛】本题考查了角度的计算,角平分线的定义,垂直的定义,通过旋转的速度和时间可得旋转的角度,对比旋转之前的图形是解题的关键.
三、解答题:本题共8个小题,19-24每题8分,25-26每题9分,共66分。
19.(2021·广东光明区·)如图,已知平面上两条线段AB,CD及一点P,请利用尺规按下列要求作图:
(1)画射线AC,延长线段CD交线段AB于点E;
(2)连接BD,并用圆规在线段AB上求一点F,使BF=BD(保留画图痕迹);
(3)在直线AB上求作一点Q,使点Q到C,P两点的距离之和最小.
【答案】(1)见解析;(2)见解析;(3)见解析
【分析】(1)根据射线的定义,线段的延长线的定义画出图形即可.(2)以B为圆心,BD为半径作弧,交AB于点F,点F即为所求作.(3)连接PC交AB于点Q,点Q即为所求作.
【详解】解:(1)如图,射线AC,射线CE即为所求作.
(2)如图,线段BF即为所求作.(3)如图,点Q即为所求作.
【点睛】本题考查基本作图,两点之间线段最短等知识,解题的关键是明确概念,熟练掌握基本作图,属于中考常考题型.
20.(2021·西安爱知初级中学七年级月考)某种产品的形状是长方体,长为,它的展开图如图:
(1)求该长方体的宽和高;(2)某厂家要为该产品做一个包装纸箱,使每箱能装2件这种产品,并且要求没有空隙且要使该纸箱所用材料尽可能少(厚度忽略不计),请求出该纸箱的体积.
【答案】(1)长方体的宽和高分别为:cm,2cm;(2)该纸箱的体积为:cm3.
【分析】(1)设长方体的高为cm,则宽为cm,结合展开图可得再解方程可得答案;
(2)由每箱能装2件这种产品,并且要求没有空隙且要使该纸箱所用材料尽可能少,则应该让的面重叠在一起,从而可得这个长方体的纸盒的长,宽,高分别为8cm,6cm,4cm,从而可得答案.
【详解】解:(1)设长方体的高为cm,则宽为cm,所以: 解得:
所以长方体的宽和高分别为:cm,2cm.
(2)由长方体的长和宽和高分别为:,cm,2cm.
而每箱能装2件这种产品,并且要求没有空隙且要使该纸箱所用材料尽可能少,
则应该让的面重叠在一起,此时这个长方体的纸盒的长,宽,高分别为8cm,6cm,4cm.
所以该纸箱的体积为:cm3.
【点睛】本题考查的是一元一次方程的应用,长方体的认识,掌握利用长方体的展开图的特点列方程是解题的关键.
21.(2021·广东光明区·)定义:数轴上的三点,如果其中一个点与近点距离是它与远点距离的,则称该点是其他两个点的“倍分点”.例如数轴上点A,B,C所表示的数分别为﹣1,0,2,满足AB=BC,此时点B是点A,C的“倍分点”.已知点A,B,C,M,N在数轴上所表示的数如图所示.
(1)A,B,C三点中,点 是点M,N的“倍分点”;
(2)若数轴上点M是点D,A的“倍分点”,则点D对应的数有 个,分别是 ;
(3)若数轴上点N是点P,M的“倍分点”,且点P在点N的右侧,求此时点P表示的数.
【答案】(1)B;(2)4;﹣2,﹣4,1,﹣7;(3)或24
【分析】(1)利用“倍分点”的定义即可求得答案;
(2)设D点坐标为x,利用“倍分点”的定义,分两种情况讨论即可求出答案;
(3)利用“倍分点”的定义,结合点P在点N的右侧,分两种情况讨论即可求出答案.
【详解】解:(1)∵BM=0-(-3)=3,BN=6-0=6,∴BM=BN,∴点B是点M,N的“倍分点”;
(2)AM=-1-(-3)=2,设D点坐标为x,
①当DM=AM时,DM=1,∴|x-(-3)|=1,解得:x=-2或-4,
②当AM=DM时,DM=2AM=4,∴|x-(-3)|=4,解得:x=1或-7,
综上所述,则点D对应的数有4个,分别是-2,-4,1,-7,故答案为:4;-2,-4,1,-7;
(3)MN=6-(-3)=9,当PN=MN时,PN=×9=,
∵点P在点N的右侧,∴此时点P表示的数为,
当MN=PN时,PN=2MN=2×9=18,
∵点P在点N的右侧,∴此时点P表示的数为24,
综上所述,点P表示的数为或24.
【点睛】本题考查了数轴结合新定义“倍分点”,正确理解“倍分点”的含义是解决问题的关键.
22.(2021·江苏·汇文实验初中七年级月考)七年级学生小聪和小明完成了数学实验《钟面上的数学》后,制作了一个模拟钟面,如图所示,点O为模拟钟面的圆心,M、O、N在一条直线上,指针OA、OB分别从OM、ON出发绕点O转动,OA顺时针转动,OB逆时针转动,OA运动速度为每秒转动15°,OB运动速度为每秒转动5°,当一根指针与起始位置重合时,运动停止,设转动的时间为t秒(t>0),请你试着解决他们提出的下列问题:
(1)OA顺时针转动,OB逆时针转动,当t= 秒时,OA与OB第一次重合;
(2)OA顺时针转动,OB逆时针转动,当t=3秒时,∠AOB= °;
(3)若他们同时顺时针转动,t为何值时,OA与OB的夹角为20°?
(4)若他们同时顺时针转动,t为何值时,ON平分OA与OB的夹角?OA平分OB与ON的夹角?
【答案】(1) 9;(2)120;(3)16或20;(4)9,14.4.
【分析】(1)当OA与OB第一次重合时,OA与OB转过的角度之和为180°,据此得到方程,求解即可;
(2)当秒时,,,根据角的和差即可求解;
(3)设t秒后,OA与OB的夹角为20°,分类讨论:当OA与OB重合之前、当OA与OB重合之后,利用角的和差即可求解;(4)由题意可得,,,根据角平分线的定义即可求解.
【详解】解:(1)设t秒后,OA与OB第一次重合,
根据题意可得:,解得,故答案为:9;
(2)当秒时,,,
∴,故答案为:120;
(3)设t秒后,OA与OB的夹角为20°,
①当OA与OB重合之前,由题意可得:,解得;
②当OA与OB重合之后,由题意可得:,解得,
∴秒或秒时,OA与OB的夹角为20°;
(4)由题意可知,
∴,,,
当ON平分OA与OB的夹角时,即,∴,解得;
当OA平分OB与ON的夹角时,即,∴,解得.
【点睛】本题考查一元一次方程的实际应用、角的和差等,根据题意列出方程是解题的关键.
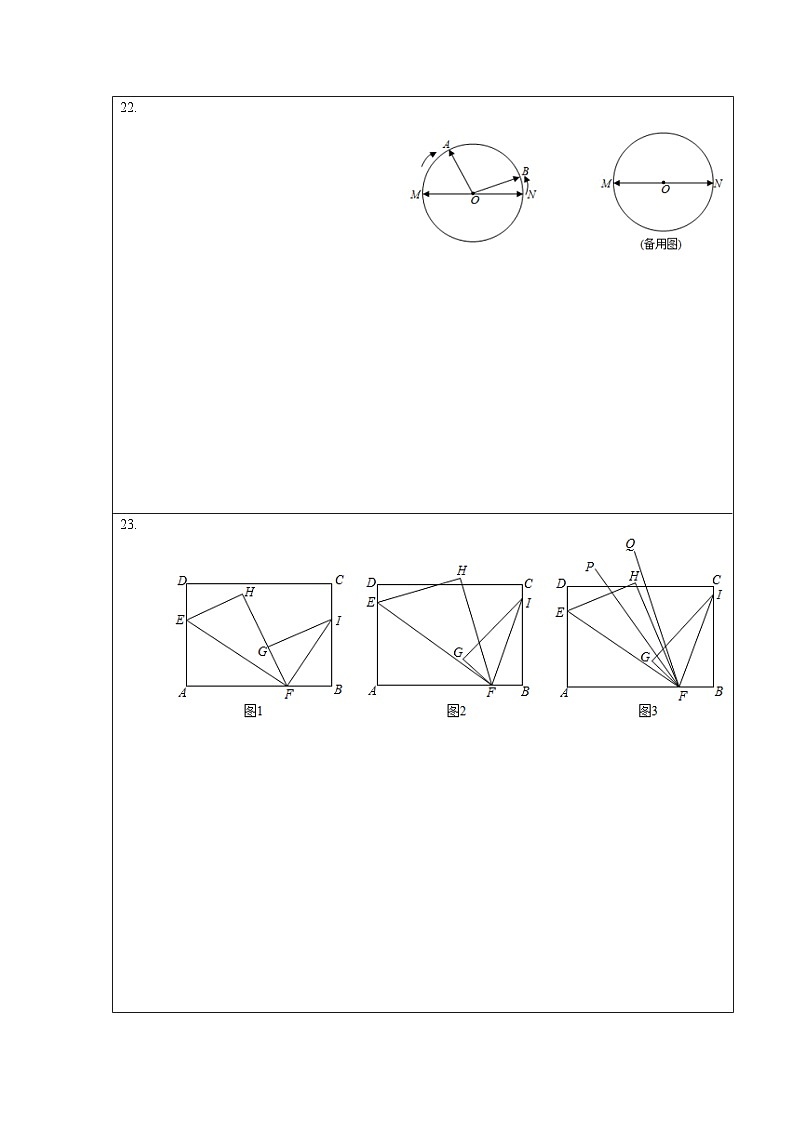
23.(2021·湖南长沙市·明德华兴中学)已知长方形纸片ABCD, E、F分别是AD、AB上的一点,点I在射线BC上、连接EF,FI,将∠A沿EF所在的直线对折,点A落在点H处,∠B沿FI所在的直线对折,点B落在点G处.(1)如图1,当HF与GF重合时,则∠EFI=_________°;(2)如图2,当重叠角∠HFG=30°时,求∠EFI的度数;(3)如图3,当∠GFI=α,∠EFH=β时,∠GFI绕点F进行逆时针旋转,且∠GFI总有一条边在∠EFH内,PF是∠GFH的角平分线,QF是∠EFI的角平分线,旋转过程中求出∠PFQ的度数(用含α,β的式子表示).
【答案】(1);(2);(3).
【分析】(1)根据折叠的性质可得∠HFE=∠AFE,∠IFG=∠IFB,再根据∠HFE+∠AFE+∠IFG+∠IFB=180°,即可得到∠EFI=∠HFE+∠IFH=90°;(2)令,,推导出x与y的和即可求得答案;
(3)先求出∠GFH,∠GFP,∠QFI,根据,即可得到答案.
【详解】(1)由折叠的性质得∠HFE=∠AFE,∠IFG=∠IFB,
∵∠HFE+∠AFE+∠IFG+∠IFB=180°,∴∠EFI=∠HFE+∠IFH=90°;
(2)令,∵30°∴30°+x,30+y,
∴180°,
即90°,∴45°,∴75°;
(3),,
∴180°,∴90°,
又∵,
.
【点睛】本题主要考查了角平分线的性质,角的计算,解题的关键在于能够熟练掌握相关知识进行求解.
24.(2021·湖南·长沙市雅礼实验中学七年级开学考试)已知∠AOD=40°,射线OC从OD出发,绕点O以20°/秒的速度逆时针旋转,旋转时间为t秒(t≤7).射线OE、OF分别平分∠AOC、∠AOD.
(1)如图①,如果t=4秒,求∠EOA的度数;
(2)如图①,若射线OC旋转时间为t秒,求∠EOF的度数(用含t的代数式表示);
(3)射线OC从OD出发时,射线OB也同时从OA出发,绕点O以10°/秒的速度逆时针旋转,射线OC、OB在旋转过程中(t≤7),若∠BOD=∠EOB,请你借助图②和备用图进行分析后,直接写出的值.
【答案】(1)60°;(2);(3)或
【分析】(1)根据角分线的定义、旋转的过程即可求解;
(2)根据旋转的过程和角分线的定义进行角的计算即可;
(3)分两种情况讨论:OB落在不同位置时进行角的计算即可.
【详解】解:(1)如图①,根据题意,得∠DOC=4×20°=80°
∴∠AOC=∠AOD+∠DOC=40°+80°=120°,
∵射线OE平分∠AOC,∴,
答:∠EOA的度数为60°.
(2)根据题意,得∠COD=(20t)°∴∠AOC=(40+20t)°
∵射线OE、OF分别平分∠AOC、∠AOD,
∴,∠AOF=20°,
∴∠EOF=∠AOE﹣∠AOF=(10t)°,
答:∠EOF的度数为.
(3)∵射线OE、OF分别平分∠AOC、∠AOD,
根据题意,得∴,
①如图②:当OB落在OF和OD之间时,∠BOD=40﹣10t,40﹣10t=10,解得t=3.
②如图3:当OB落在OD和OE之间时,∠BOD=10t﹣40,10t﹣40=10解得t=5.
当t=3时,的值为,当t=5时,的值为.答:的值为或.
【点睛】此题考查了几何图形中角的和差倍分运算,角平分线的定义以及一元一次方程的应用,掌握角平分线的定义以及和差的关系是解题的关键.
25.(2021·湖北武汉市·七年级期中)(问题背景)在数轴上,点表示数在原点的左边,点表示的数在原点的右边,如图1,所示,则有:①;②线段的长度等于.
(问题解决)点、点、点在数轴上的位置如图2所示,三点对应的数分别为,、.
①线段的长度为_________;
②若点为线段的中点,则点表示的数是________;
③化简:.
(关联运用)①已知:点、点、点、点在数轴上的位置如图3所示,点对应的数为,点对应的数为,若定长线段沿数轴正方向以每秒个单位长度匀速运动,经过原点需要1秒,完全经过线段需要2秒,求的值;②已知,当式子取最小值时,相应的的取值范围是_________,式子的最小值是__________.(用含、的式子表示)
【答案】(问题解决)①8;②t+1;③;(关联运用)①;②;
【分析】(问题解决)①根据题意,及数轴上两点间的距离解题;②根据中点公式及两点间的距离解题;
③先判断每个绝对值内的数的正负性,再结合绝对值的性质化简即可;
(关联运用)①设表示的数为,则表示的数为,分别计算t秒时点E、F表示的数,再根据与重合时或和重合时,列式解题即可;
②数轴上动点到四个点的距离之和最小,即点处在四个点的中间区域,即,再代入式子,化简绝对值解题即可.
【详解】(问题解决)①由问题背景:线段AB的长为,可知MN=故答案:8;
②Q为MN中点设为x,则MQ=,MQ=,,故答案为:t+1;
③观察数轴可知,
(关联运用)①∵经过原点需要1秒,∴,
设表示的数为,则表示的数为,秒时,:,:,
当与重合时,,;当和重合时,,.
由题知:,,,.
②表示到、、、(数轴上从左至右排列)之间的距离之和(注意:距离和最小,在最中间), 则当时,距离之和有最小值故答案为:;.
【点睛】本题考查数轴上两点间的距离,其中涉及数轴上的动点问题,线段的中点、绝对值的化简等知识,是重要考点,难度一般,掌握相关知识是解题关键.
26.(2021·浙江杭州·七年级期中)已知将一副三角板()如图1摆放,点O、A、C在一条直线上.将直角三角板绕点O逆时针方向转动,变化摆放如图位置.
(1)如图1,当点O、A、C在同一条直线上时,_______度;如图2,若要恰好平分,则_______度;(2)如图3,当三角板摆放在内部时,作射线平分,射线平分,如果三角板在内绕点O任意转动,的度数是否发生变化?如果不变,求其值;如果变化,说明理由.(3)当三角板从图1的位置开始,绕点O逆时针方向旋转一周,保持射线平分、射线平分(),在旋转过程中,(2)中的结论是否保持不变?如果保持不变,请说明理由;如果变化,请说明变化的情况和结果(即旋转角度a在什么范围内时的度数是多少).
【答案】(1)60,75;(2),理由见详解;(3)①当时,;②当时,或120°,③当时,;④当时,或60°;⑤当时,
【分析】(1)由题意易得,然后根据角平分线的定义及角的和差关系可进行求解;
(2)由题意易得,,进而可得,然后问题可求解;
(3)设旋转角度为,根据题意可得:,①当时,②当时,即为平角,③当时,④当时,则,⑤当时,然后进行分类求解即可.
【详解】解:(1)由题意得:,∴,
∵恰好平分,∴,
∴;故答案为60,75;
(2)的度数不发生变化,理由如下:
∵射线平分,射线平分,∴,
∵,∴,
∴,∴;
(3)设旋转角度为,根据题意可得:,
∵射线平分,射线平分,∴,
①当时,如图所示:
∴,
②当时,即为平角,可分为:当点M在OB上,如图所示:
∴,∴;
当点M在BO的延长线时,如图所示:
∴;
③当时,如图所示:
∴,
∴,解得:,
∴;
④当时,则,如图所示:
∴当ON平分在∠BOD的左边时,则,当ON平分在∠BOD的右边时,则;
⑤当时,如图所示:
∴,
∴.
【点睛】本题主要考查角平分线的定义及平角的意义,熟练掌握角平分线的定义及平角的意义是解题关键.
第四章 几何图形初步(人教版)
选拔卷
(考试时间:90分钟 试卷满分:120分)
一、选择题:本题共10个小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(2021·北京二中七年级期末)有5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形折叠后能成为一个封闭的正方体盒子,你不能选择图中A,B,C,D中的( )位置拼接正方形.
A.A B.B C.C D.D
【答案】A
【分析】结合正方体的平面展开图的特征,只要折叠后能围成正方体即可.
【详解】解:如图所示:
根据立方体的展开图可知,不能选择图中A的位置接正方形.故选:A.
【点睛】此题主要考查了应用与设计作图.正方体的平面展开图共有11种,应灵活掌握,不能死记硬背.
2.(2021·浙江省义乌市望道中学七年级月考)如图,已知的顶点在直线上,平分,平分,则的度数是( )
A. B. C. D.
【答案】D
【分析】运用角平分线的定义算出∠FOE=2∠COF,再由∠COE为直角,可求出∠COF的度数,再求出∠AOF的度数,最后可求得∠BOE的度数.
【详解】解:∵平分∴∠AOF=∠FOE
∵平分∴∠AOF=2∠COF∴∠FOE=2∠COF
又∠COE是直角∴∴∠AOF=∠FOE=60°
∴故选:D.
【点睛】此题考查角平分线的定义和角的有关运算.发现组成RT∠COE的两个角:∠FOE=2∠COF是解决问题的关键.
3.(2020·广东省初一月考)如图,是一个带有方形空洞和圆形空洞的儿童玩具,如果用下列几何体作为塞子,那么既可以堵住方形空洞,又可以堵住圆形空洞的几何体是( )
A. B. C. D.
【答案】B
【解析】圆柱从上边看是一个圆,从正面看是一个正方形,既可以堵住方形空洞,又可以堵住圆形空洞,故选B.
考点:简单几何体的三视图.
4.(2021·山西吕梁市·七年级期末)有一种正方体如图所示,下列图形是该正方体的展开图的是( )
A. B. C. D.
【答案】D
【分析】根据题意,三个图形有一个公共顶点,其中绿色长方形与等腰直角三角形有一条公共边,据此逐项分析解题.
【详解】解:A.折叠后,三个图形没有公共顶点,故A不符合题意;
B.折叠后,长方形与普通三角形是相对面,故B不符合题意;C.折叠后,两个三角形是相对面,故C不符合题意;D.折叠后,三个图形有一个公共顶点,其中绿色长方形与等腰直角三角形有一条公共边,故D符合题意,故选:D.
【点睛】本题考查正方体的表面展开图,是重要考点,难度较易,掌握相关知识是解题关键.
5.(2021·全国·七年级专题练习)如图,为直线上一点,,平分,平分, 平分,下列结论:①; ②;
③; ④ 其中正确的个数有( )
A.个 B.个 C.个 D.个
【答案】C
【分析】根据余角和补角的定义以及角平分线的定义,计算出各选项的结果判断即可.
【详解】解:∵平分,平分,∴,,
∴,
∵,∴,∴,∴,
∵,∴,故①正确;
∵,∵平分,平分,
∴,∴,故②正确;
∵,∴,
∴,故③正确;
∵不能证明,故④错误;∴正确的选项有3个;故选:C.
【点睛】本题考查了同角的补角相等,同角的余角相等,角的平分线,以及角的运算,解题的关键是熟练掌握角的平分线性质,余角和补角的定义,从而进行计算.
6.(2021·江苏连云港市·七年级期末)如图,图1是一个三阶金字塔魔方,它是由若干个小三棱锥堆成的一个大三棱锥(图2),把大三棱锥的四个面都涂上颜色.若把其中1个面涂色的小三棱锥叫中心块,2个面涂色的叫棱块,3个面涂色的叫角块,则三阶金字塔魔方中“(棱块数)+(角块数)-(中心块数)”得( )
A.2 B.-2 C.0 D.4
【答案】B
【分析】根据三阶魔方的特征,分别求出棱块数、角块数、中心块数,再计算即可.
【详解】解:如图所示:
∵3个面涂色的小三棱锥为四个顶点处的三棱锥,共4个,∴角块有4个;
∵2个面涂色的小三棱锥为每两个面的连接处,共6个,∴棱块有6个;
∵1个面涂色的小三棱锥为每个面上不与其他面连接的部分,即图中的阴影部分的3个,
∴中心块有:(个);∴(棱块数)+(角块数)(中心块数)=;选:B.
【点睛】本题考查了三阶魔方的特征,认识立体图形,图形的规律;解题的关键是正确的认识三阶魔方的特征,从而进行解题.
7.(2021·扬州市梅岭中学七年级期末)如图1,线段OP表示一条拉直的细线,A、B两点在线段OP上,且OA:AP=1:2,OB:BP=2:7.若先固定A点,将OA折向AP,使得OA重叠在AP上;如图2,再从图2的B点及与B点重叠处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比是( )
A.1:1:2 B.2:2:5 C.2:3:4 D.2:3:5
【答案】B
【分析】根据题意设OB的长度为2a,则BP的长度为7a,OP的长度为9a,从而根据比值可以得到图一中各线段的长,根据题意可以求出折叠后,再剪开各线段的长度,从而可以求得三段细线由小到大的长度比,本题得以解决.
【详解】解:设OB的长度为2a,则BP的长度为7a,OP的长度为9a,
∵OA:AP=1:2,∴OA=3a,AP=6a,
又∵先固定A点,将OA折向AP,使得OA重叠在AP上,如图2,再从图2 的B点及与B点重迭处一起剪开,使得细线分成三段,
∴这三段从小到大的长度分别是:2a、2a、5a,
∴此三段细线由小到大的长度比为:2a:2a:5a=2:2:5,故选:B.
【点睛】本题考查比较线段的长短,解题的关键是理解题意,求出各线段的长度.
8.(2021·四川成都市·成都实外)如图,将长方形纸片ABCD的∠C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若∠BFE=3∠BFH,∠BFH=20°,则∠GFH的度数是( )
A.85° B.90° C.95° D.100°
【答案】D
【分析】根据折叠求出∠CFG=∠EFG=∠CFE,根据∠BFE=3∠BFH,∠BFH=20°,即可求出∠GFH=∠GFE+∠HFE的度数.
【详解】解:∵将长方形纸片ABCD的角C沿着GF折叠(点F在BC上,不与B,使点C落在长方形内部点E处,∴∠CFG=∠EFG=∠CFE,
∵∠BFE=3∠BFH,∠BFH=20°,∴∠BFE=60°,∴∠CFE=120°,∴∠GFE=60°,
∵∠EFH=∠EFB﹣∠BFH,∴∠EFH==40°,∴∠GFH=∠GFE+∠EFH=60°+40°=100°.选:D.
【点睛】本题考查了角的计算,折叠的性质,角度的倍数关系,主要考查学生的推理和计算能力.
9.(2021·河南省淮滨县第一中学七年级期末)如图,直线相交于点,平分,射线将分成了角度数之比为的两个角,则的大小为( )
A. B. C.或 D.或
【答案】C
【分析】设∠DOE=x°,∠BOD=2x°或x°,表示出其他角,根据平角列方程即可.
【详解】解:设∠DOE=x°,射线将分成了角度数之比为的两个角,
当∠DOE:∠BOD=2:1时,∠BOD=x°,=x°,
∵平分,∴=x°,
∵∠COD=180°,∴x+x+90+ x=180,解得,x=45;∠COF=2∠AOC=45°;
当∠BOD: ∠DOE =2:1时,∠BOD=2x°,=2x°,同理, =2x°,
2x+2x+90+ x=180,解得:x=18,∠COF=2∠AOC=72°;故选:C.
【点睛】本题考查了角的运算、角的度量和角平分线,解题关键是根据角度比设未知数,表示出其他角,然后根据平角列方程,注意:分类讨论.
10.(2021·全国·九年级专题练习)如图,点M在线段AN的延长线上,且线段MN=20,第一次操作:分别取线段AM和AN的中点;第二次操作:分别取线段和的中点;第三次操作:分别取线段和的中点;……连续这样操作10次,则每次的两个中点所形成的所有线段之和( )
A. B. C. D.
【答案】A
【分析】根据,分别为的中点,求出的长度,再由的长度求出的长度,找到的规律即可求出的值.
【详解】解:∵,分别为的中点,
∴,
∵分别为的中点,
∴,根据规律得到,
∴,故选A.
【点睛】本题是对线段规律性问题的考查,准确根据题意找出规律是解决本题的关键,相对较难.
二、填空题:本题共8个小题,每题3分,共24分。
11.(2021·河北保定师范附属学校九年级期末)如图2是图1中长方体的三视图,若用S表示面积,,,则
【答案】20
【分析】由主视图和左视图的宽为x,结合两者的面积得出俯视图的长和宽,从而得出答案.
【详解】解:∵S主=5x,S左=4x,且主视图和左视图的宽为x,
∴俯视图的长为5,宽为4,则俯视图的面积S俯=5×4=20.
【点睛】本题主要考查由三视图判断几何体,解题的关键是根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,以及几何体的长、宽、高.
12.(2021·浙江浙江省·)已知三点在同一条直线上,且线段,点分别是线段的中点点F是线段的中点,则_______.
【答案】或
【分析】根据中点定义求出BD、BE的长度,然后分①点C在AB的延长线上时,求出DE的长度,再根据中点定义求出EF的长,然后根据BF=BE-EF代入数据进行计算即可得解;②点C在AB的反向延长线上时,求出DE的长度,再根据中点定义求出EF的长,然后根据BF=BE-EF代入数据进行计算即可得解.
【详解】解:、分别是线段、的中点,,,
,,
①如图1,点在的延长线上时,,
点是线段的中点,,此时,;
②如图2,点在的反向延长线上时,,
点是线段的中点,,此时,,
综上所述,或.故答案为:或.
【点睛】本题考查两点间的距离,线段中点的定义,难点在于要分情况讨论,作出图形更形象直观.
13.(2021·山西运城市·七年级期末)一个几何体由一些大小相同的小正方体搭成,从正面和左面看到的这个几何体的形状如图所示,则搭成该几何体的小正方体的个数最少是___________.
【答案】4
【分析】由主视图和左视图确定俯视图的形状,再判断最少的正方体的个数.
【详解】解:由题中所给出的主视图知物体共3列,且都是最高两层;由左视图知共3行,
所以小正方体的个数最少的几何体为:
第一列第一行1个小正方体,第二列第二行2个小正方体,第三列第三行1个小正方体,其余位置没有小正方体.即组成这个几何体的小正方体的个数最少为:1+2+1=4个.故答案为:4.
【点睛】本题考查了学生对三视图的掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就更容易得到答案.
14.(2020·四川省初一期中)瑞士著名数学家欧拉发现:简单多面体的顶点数V、面数F及棱数E之间满足一种有趣的关系:V+F﹣E=2,这个关系式被称为欧拉公式.比如:正二十面体(如右图),是由20个等边三角形所组成的正多面体,已知每个顶点处有5条棱,则可以通过欧拉公式算出正二十面体的顶点为_____个.那么一个多面体的每个面都是五边形,每个顶点引出的棱都有3条,它是一个_____面体.
【答案】12. 12.
【分析】①设出正二十面体的顶点为n个,则棱有条.利用欧拉公式构建方程即可解决问题.②设顶点数V、棱数E、面数F、每个点都属于三个面,每条边都属于两个面,利用欧拉公式构建方程即可解决问题.
【解析】解:①设出正二十面体的顶点为n个,则棱有条.
由题意F=20,∴n+10﹣=2,解得n=12.
②设顶点数V,棱数E,面数F,每个点属于三个面,每条边属于两个面
由每个面都是五边形,则就有E=,V=
由欧拉公式:F+V﹣E=2,代入:F+﹣=2.化简整理:F=12 所以:E=30,V=20
即多面体是12面体.棱数是30,面数是12,故答案为12,12.
【点睛】本题考查欧拉公式的应用,解题的关键是弄清题意、利用等量关系列出方程是解答本题的关键.
15.(2021·全国·七年级专题练习)如图,点O是钟面的中心,射线正好落在3:00时针的位置.当时钟从2:00走到3:00,则经过___________分钟,时针,分针,与所在的三条射线中,其中一条射线是另外两条射线所夹角的角平分线.
【答案】6或
【分析】分两种情况讨论:当时针为角平分线和OC为角平分线进行计算即可.
【详解】设时针为OB,分针为OA. 当时针为OB为角平分线时,如图1所示:
设经过x分钟,OB为角平分线,则∠AOB=60゜-6x゜+,∠BOC=30゜-,依题意得:60-6x+=30-解得x=6;
当时针为OC为角平分线时,如图2所示:
设经过x分钟,OC为角平分线,则∠AOC=6x゜-90゜,∠BOC=30゜-,
依题意得:6x-90=30-解得x=;
综合上述可得:经过6分钟或分钟时,时针,分针,与所在的三条射线中,其中一条射线是另外两条射线所夹角的角平分线.
故答案为:6或.
【点睛】考查了一元一次方程的应用和角平分线的性质,解题关键是分两种情况讨论:当时针为角平分线和OC为角平分线和利用方程求得其角度.
16.(2020·辽宁皇姑·七年级期末)如图,在平面内,点是直线上一点,,射线不动,射线,同时开始绕点顺时针转动,射线首次回到起始位置时两线同时停止转动,射线,的转动速度分别为每秒和每秒.若转动秒时,射线,,中的一条是另外两条组成角的角平分线,则______秒.
【答案】4或5
【分析】根据已知条件可知,在第t秒时,射线OA转过的角度为40°t,射线OB转过的角度为20°t,然后按照OA、OB、OC三条射线构成相等的角分三种情况讨论:①当OA平分∠BOC;②当OC平分∠AOB;③当OB平分∠AOC,分别列方程即可求出t的值.
【详解】解:根据题意,在第t秒时,射线OA转过的角度为40°t,射线OB转过的角度为20°t,
①当OA,OB转到OA′,OB′的位置时,如图①所示,∠A′OC=∠A′OB′,
∵∠A′OC=180°-40°t,∠A′OB′=∠AOA′-∠AOB-∠BOB′=40°t-60°-20°t=20°t-60°,
∴180°-40°t =20°t-60°,即t=4;
②当OA,OB转到OA′,OB′的位置时,如图②所示,∠A′OC=∠B′OC,
∵∠A′OC=40°t-180°,∠B′OC=180°-∠AOB-∠BOB′=180°-60°-20°t=120°-20°t,
∴40°t-180°=120°-20°t,即t=5;
③当OA,OB转到OA′,OB′的位置时,如图③,∠B′OC=∠A′OB′,
∵∠B′OC=20°t-120°,∠A′OB′=∠A′OC=(180°-∠AOA′)=[180°-(360°-40°t)]=20°t-90°,
∴20°t-120°=20°t-90°,此时方程不成立.
综上所述:t的值为4或5.故答案:4或5.
【点睛】题主要考查角的和、差关系,难点是找出变化过程中的不变量,需要结合图形来计算,在计算分析的过程中注意动手操作,在旋转的过程中得到不变的量.
17.(2021·沙坪坝区·重庆南开中学七年级月考)如图,数轴上有两点,点C从原点O出发,以每秒的速度在线段上运动,点D从点B出发,以每秒的速度在线段上运动.在运动过程中满足,若点M为直线上一点,且,则的值为_______.
【答案】1或
【分析】设点A在数轴上表示的数为a,点B在数轴上表示的数为b,设运动的时间为t秒,由OD=4AC得a与b的关系,再根据点M在直线AB的不同的位置分4种情况进行解答,①若点M在点B的右侧时,②若点M在线段BO上时,③若点M在线段OA上时,④若点M在点A的左侧时,分别表示出AM、BM、OM,由AM-BM=OM得到t、a、b之间的关系,再计算的值即可.
【详解】设运动的时间为t秒,点M表示的数为m
则OC=t,BD=4t,即点C在数轴上表示的数为-t,点D在数轴上表示的数为b-4t,∴AC=-t-a,OD=b-4t,
由OD=4AC得,b-4t=4(-t-a),即:b=-4a,
①若点M在点B的右侧时,如图1所示:
由AM-BM=OM得,m-a-(m-b)=m,即:m=b-a;∴
②若点M在线段BO上时,如图2所示:
由AM-BM=OM得,m-a-(b-m)=m,即:m=a+b;∴
③若点M在线段OA上时,如图3所示:
由AM-BM=OM得,m-a-(b-m)=-m,即:
∵此时m<0,a<0,∴此种情况不符合题意舍去;
④若点M在点A的左侧时,如图4所示:
由AM-BM=OM得,a-m-(b-m)=-m,即:m=b-a=-5a;而m<0,b-a>0,因此,不符合题意舍去,
综上所述,的值为1或.
【点睛】考查数轴表示数的意义,掌握数轴上两点之间距离的计算方法是正确解答的关键,分类讨论和整体代入在解题中起到至关重要的作用.
18.(2021·重庆八中七年级期末)如图,直线AB⊥OC于点O,∠AOP=40°,三角形EOF其中一个顶点与点O重合,∠EOF=100°,OE平分∠AOP,现将三角形EOF以每秒6°的速度绕点O逆时针旋转至三角形E′OF′,同时直线PQ也以每秒9°的速度绕点O顺时针旋转至P′Q′,设运动时间为m秒(0≤m≤20),当直线P′Q′平分∠E′OF′时,则∠COP′=___.
【答案】或
【分析】由题意,分两种情况讨论,当平分时,当平分时作出图形,分别画出对应图,对比开始时刻的角度,通过角度的加减计算即可.
【详解】平分,,
以每秒的速度绕点O逆时针旋转,以每秒的速度点O顺时针旋转,
①如图1中,当平分时,
解得
,
②如图2,当平分时,
解得
故答案为:或
【点睛】本题考查了角度的计算,角平分线的定义,垂直的定义,通过旋转的速度和时间可得旋转的角度,对比旋转之前的图形是解题的关键.
三、解答题:本题共8个小题,19-24每题8分,25-26每题9分,共66分。
19.(2021·广东光明区·)如图,已知平面上两条线段AB,CD及一点P,请利用尺规按下列要求作图:
(1)画射线AC,延长线段CD交线段AB于点E;
(2)连接BD,并用圆规在线段AB上求一点F,使BF=BD(保留画图痕迹);
(3)在直线AB上求作一点Q,使点Q到C,P两点的距离之和最小.
【答案】(1)见解析;(2)见解析;(3)见解析
【分析】(1)根据射线的定义,线段的延长线的定义画出图形即可.(2)以B为圆心,BD为半径作弧,交AB于点F,点F即为所求作.(3)连接PC交AB于点Q,点Q即为所求作.
【详解】解:(1)如图,射线AC,射线CE即为所求作.
(2)如图,线段BF即为所求作.(3)如图,点Q即为所求作.
【点睛】本题考查基本作图,两点之间线段最短等知识,解题的关键是明确概念,熟练掌握基本作图,属于中考常考题型.
20.(2021·西安爱知初级中学七年级月考)某种产品的形状是长方体,长为,它的展开图如图:
(1)求该长方体的宽和高;(2)某厂家要为该产品做一个包装纸箱,使每箱能装2件这种产品,并且要求没有空隙且要使该纸箱所用材料尽可能少(厚度忽略不计),请求出该纸箱的体积.
【答案】(1)长方体的宽和高分别为:cm,2cm;(2)该纸箱的体积为:cm3.
【分析】(1)设长方体的高为cm,则宽为cm,结合展开图可得再解方程可得答案;
(2)由每箱能装2件这种产品,并且要求没有空隙且要使该纸箱所用材料尽可能少,则应该让的面重叠在一起,从而可得这个长方体的纸盒的长,宽,高分别为8cm,6cm,4cm,从而可得答案.
【详解】解:(1)设长方体的高为cm,则宽为cm,所以: 解得:
所以长方体的宽和高分别为:cm,2cm.
(2)由长方体的长和宽和高分别为:,cm,2cm.
而每箱能装2件这种产品,并且要求没有空隙且要使该纸箱所用材料尽可能少,
则应该让的面重叠在一起,此时这个长方体的纸盒的长,宽,高分别为8cm,6cm,4cm.
所以该纸箱的体积为:cm3.
【点睛】本题考查的是一元一次方程的应用,长方体的认识,掌握利用长方体的展开图的特点列方程是解题的关键.
21.(2021·广东光明区·)定义:数轴上的三点,如果其中一个点与近点距离是它与远点距离的,则称该点是其他两个点的“倍分点”.例如数轴上点A,B,C所表示的数分别为﹣1,0,2,满足AB=BC,此时点B是点A,C的“倍分点”.已知点A,B,C,M,N在数轴上所表示的数如图所示.
(1)A,B,C三点中,点 是点M,N的“倍分点”;
(2)若数轴上点M是点D,A的“倍分点”,则点D对应的数有 个,分别是 ;
(3)若数轴上点N是点P,M的“倍分点”,且点P在点N的右侧,求此时点P表示的数.
【答案】(1)B;(2)4;﹣2,﹣4,1,﹣7;(3)或24
【分析】(1)利用“倍分点”的定义即可求得答案;
(2)设D点坐标为x,利用“倍分点”的定义,分两种情况讨论即可求出答案;
(3)利用“倍分点”的定义,结合点P在点N的右侧,分两种情况讨论即可求出答案.
【详解】解:(1)∵BM=0-(-3)=3,BN=6-0=6,∴BM=BN,∴点B是点M,N的“倍分点”;
(2)AM=-1-(-3)=2,设D点坐标为x,
①当DM=AM时,DM=1,∴|x-(-3)|=1,解得:x=-2或-4,
②当AM=DM时,DM=2AM=4,∴|x-(-3)|=4,解得:x=1或-7,
综上所述,则点D对应的数有4个,分别是-2,-4,1,-7,故答案为:4;-2,-4,1,-7;
(3)MN=6-(-3)=9,当PN=MN时,PN=×9=,
∵点P在点N的右侧,∴此时点P表示的数为,
当MN=PN时,PN=2MN=2×9=18,
∵点P在点N的右侧,∴此时点P表示的数为24,
综上所述,点P表示的数为或24.
【点睛】本题考查了数轴结合新定义“倍分点”,正确理解“倍分点”的含义是解决问题的关键.
22.(2021·江苏·汇文实验初中七年级月考)七年级学生小聪和小明完成了数学实验《钟面上的数学》后,制作了一个模拟钟面,如图所示,点O为模拟钟面的圆心,M、O、N在一条直线上,指针OA、OB分别从OM、ON出发绕点O转动,OA顺时针转动,OB逆时针转动,OA运动速度为每秒转动15°,OB运动速度为每秒转动5°,当一根指针与起始位置重合时,运动停止,设转动的时间为t秒(t>0),请你试着解决他们提出的下列问题:
(1)OA顺时针转动,OB逆时针转动,当t= 秒时,OA与OB第一次重合;
(2)OA顺时针转动,OB逆时针转动,当t=3秒时,∠AOB= °;
(3)若他们同时顺时针转动,t为何值时,OA与OB的夹角为20°?
(4)若他们同时顺时针转动,t为何值时,ON平分OA与OB的夹角?OA平分OB与ON的夹角?
【答案】(1) 9;(2)120;(3)16或20;(4)9,14.4.
【分析】(1)当OA与OB第一次重合时,OA与OB转过的角度之和为180°,据此得到方程,求解即可;
(2)当秒时,,,根据角的和差即可求解;
(3)设t秒后,OA与OB的夹角为20°,分类讨论:当OA与OB重合之前、当OA与OB重合之后,利用角的和差即可求解;(4)由题意可得,,,根据角平分线的定义即可求解.
【详解】解:(1)设t秒后,OA与OB第一次重合,
根据题意可得:,解得,故答案为:9;
(2)当秒时,,,
∴,故答案为:120;
(3)设t秒后,OA与OB的夹角为20°,
①当OA与OB重合之前,由题意可得:,解得;
②当OA与OB重合之后,由题意可得:,解得,
∴秒或秒时,OA与OB的夹角为20°;
(4)由题意可知,
∴,,,
当ON平分OA与OB的夹角时,即,∴,解得;
当OA平分OB与ON的夹角时,即,∴,解得.
【点睛】本题考查一元一次方程的实际应用、角的和差等,根据题意列出方程是解题的关键.
23.(2021·湖南长沙市·明德华兴中学)已知长方形纸片ABCD, E、F分别是AD、AB上的一点,点I在射线BC上、连接EF,FI,将∠A沿EF所在的直线对折,点A落在点H处,∠B沿FI所在的直线对折,点B落在点G处.(1)如图1,当HF与GF重合时,则∠EFI=_________°;(2)如图2,当重叠角∠HFG=30°时,求∠EFI的度数;(3)如图3,当∠GFI=α,∠EFH=β时,∠GFI绕点F进行逆时针旋转,且∠GFI总有一条边在∠EFH内,PF是∠GFH的角平分线,QF是∠EFI的角平分线,旋转过程中求出∠PFQ的度数(用含α,β的式子表示).
【答案】(1);(2);(3).
【分析】(1)根据折叠的性质可得∠HFE=∠AFE,∠IFG=∠IFB,再根据∠HFE+∠AFE+∠IFG+∠IFB=180°,即可得到∠EFI=∠HFE+∠IFH=90°;(2)令,,推导出x与y的和即可求得答案;
(3)先求出∠GFH,∠GFP,∠QFI,根据,即可得到答案.
【详解】(1)由折叠的性质得∠HFE=∠AFE,∠IFG=∠IFB,
∵∠HFE+∠AFE+∠IFG+∠IFB=180°,∴∠EFI=∠HFE+∠IFH=90°;
(2)令,∵30°∴30°+x,30+y,
∴180°,
即90°,∴45°,∴75°;
(3),,
∴180°,∴90°,
又∵,
.
【点睛】本题主要考查了角平分线的性质,角的计算,解题的关键在于能够熟练掌握相关知识进行求解.
24.(2021·湖南·长沙市雅礼实验中学七年级开学考试)已知∠AOD=40°,射线OC从OD出发,绕点O以20°/秒的速度逆时针旋转,旋转时间为t秒(t≤7).射线OE、OF分别平分∠AOC、∠AOD.
(1)如图①,如果t=4秒,求∠EOA的度数;
(2)如图①,若射线OC旋转时间为t秒,求∠EOF的度数(用含t的代数式表示);
(3)射线OC从OD出发时,射线OB也同时从OA出发,绕点O以10°/秒的速度逆时针旋转,射线OC、OB在旋转过程中(t≤7),若∠BOD=∠EOB,请你借助图②和备用图进行分析后,直接写出的值.
【答案】(1)60°;(2);(3)或
【分析】(1)根据角分线的定义、旋转的过程即可求解;
(2)根据旋转的过程和角分线的定义进行角的计算即可;
(3)分两种情况讨论:OB落在不同位置时进行角的计算即可.
【详解】解:(1)如图①,根据题意,得∠DOC=4×20°=80°
∴∠AOC=∠AOD+∠DOC=40°+80°=120°,
∵射线OE平分∠AOC,∴,
答:∠EOA的度数为60°.
(2)根据题意,得∠COD=(20t)°∴∠AOC=(40+20t)°
∵射线OE、OF分别平分∠AOC、∠AOD,
∴,∠AOF=20°,
∴∠EOF=∠AOE﹣∠AOF=(10t)°,
答:∠EOF的度数为.
(3)∵射线OE、OF分别平分∠AOC、∠AOD,
根据题意,得∴,
①如图②:当OB落在OF和OD之间时,∠BOD=40﹣10t,40﹣10t=10,解得t=3.
②如图3:当OB落在OD和OE之间时,∠BOD=10t﹣40,10t﹣40=10解得t=5.
当t=3时,的值为,当t=5时,的值为.答:的值为或.
【点睛】此题考查了几何图形中角的和差倍分运算,角平分线的定义以及一元一次方程的应用,掌握角平分线的定义以及和差的关系是解题的关键.
25.(2021·湖北武汉市·七年级期中)(问题背景)在数轴上,点表示数在原点的左边,点表示的数在原点的右边,如图1,所示,则有:①;②线段的长度等于.
(问题解决)点、点、点在数轴上的位置如图2所示,三点对应的数分别为,、.
①线段的长度为_________;
②若点为线段的中点,则点表示的数是________;
③化简:.
(关联运用)①已知:点、点、点、点在数轴上的位置如图3所示,点对应的数为,点对应的数为,若定长线段沿数轴正方向以每秒个单位长度匀速运动,经过原点需要1秒,完全经过线段需要2秒,求的值;②已知,当式子取最小值时,相应的的取值范围是_________,式子的最小值是__________.(用含、的式子表示)
【答案】(问题解决)①8;②t+1;③;(关联运用)①;②;
【分析】(问题解决)①根据题意,及数轴上两点间的距离解题;②根据中点公式及两点间的距离解题;
③先判断每个绝对值内的数的正负性,再结合绝对值的性质化简即可;
(关联运用)①设表示的数为,则表示的数为,分别计算t秒时点E、F表示的数,再根据与重合时或和重合时,列式解题即可;
②数轴上动点到四个点的距离之和最小,即点处在四个点的中间区域,即,再代入式子,化简绝对值解题即可.
【详解】(问题解决)①由问题背景:线段AB的长为,可知MN=故答案:8;
②Q为MN中点设为x,则MQ=,MQ=,,故答案为:t+1;
③观察数轴可知,
(关联运用)①∵经过原点需要1秒,∴,
设表示的数为,则表示的数为,秒时,:,:,
当与重合时,,;当和重合时,,.
由题知:,,,.
②表示到、、、(数轴上从左至右排列)之间的距离之和(注意:距离和最小,在最中间), 则当时,距离之和有最小值故答案为:;.
【点睛】本题考查数轴上两点间的距离,其中涉及数轴上的动点问题,线段的中点、绝对值的化简等知识,是重要考点,难度一般,掌握相关知识是解题关键.
26.(2021·浙江杭州·七年级期中)已知将一副三角板()如图1摆放,点O、A、C在一条直线上.将直角三角板绕点O逆时针方向转动,变化摆放如图位置.
(1)如图1,当点O、A、C在同一条直线上时,_______度;如图2,若要恰好平分,则_______度;(2)如图3,当三角板摆放在内部时,作射线平分,射线平分,如果三角板在内绕点O任意转动,的度数是否发生变化?如果不变,求其值;如果变化,说明理由.(3)当三角板从图1的位置开始,绕点O逆时针方向旋转一周,保持射线平分、射线平分(),在旋转过程中,(2)中的结论是否保持不变?如果保持不变,请说明理由;如果变化,请说明变化的情况和结果(即旋转角度a在什么范围内时的度数是多少).
【答案】(1)60,75;(2),理由见详解;(3)①当时,;②当时,或120°,③当时,;④当时,或60°;⑤当时,
【分析】(1)由题意易得,然后根据角平分线的定义及角的和差关系可进行求解;
(2)由题意易得,,进而可得,然后问题可求解;
(3)设旋转角度为,根据题意可得:,①当时,②当时,即为平角,③当时,④当时,则,⑤当时,然后进行分类求解即可.
【详解】解:(1)由题意得:,∴,
∵恰好平分,∴,
∴;故答案为60,75;
(2)的度数不发生变化,理由如下:
∵射线平分,射线平分,∴,
∵,∴,
∴,∴;
(3)设旋转角度为,根据题意可得:,
∵射线平分,射线平分,∴,
①当时,如图所示:
∴,
②当时,即为平角,可分为:当点M在OB上,如图所示:
∴,∴;
当点M在BO的延长线时,如图所示:
∴;
③当时,如图所示:
∴,
∴,解得:,
∴;
④当时,则,如图所示:
∴当ON平分在∠BOD的左边时,则,当ON平分在∠BOD的右边时,则;
⑤当时,如图所示:
∴,
∴.
【点睛】本题主要考查角平分线的定义及平角的意义,熟练掌握角平分线的定义及平角的意义是解题关键.
相关资料
更多









