人教版九年级上册24.2.1 点和圆的位置关系同步练习题

这是一份人教版九年级上册24.2.1 点和圆的位置关系同步练习题，共6页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
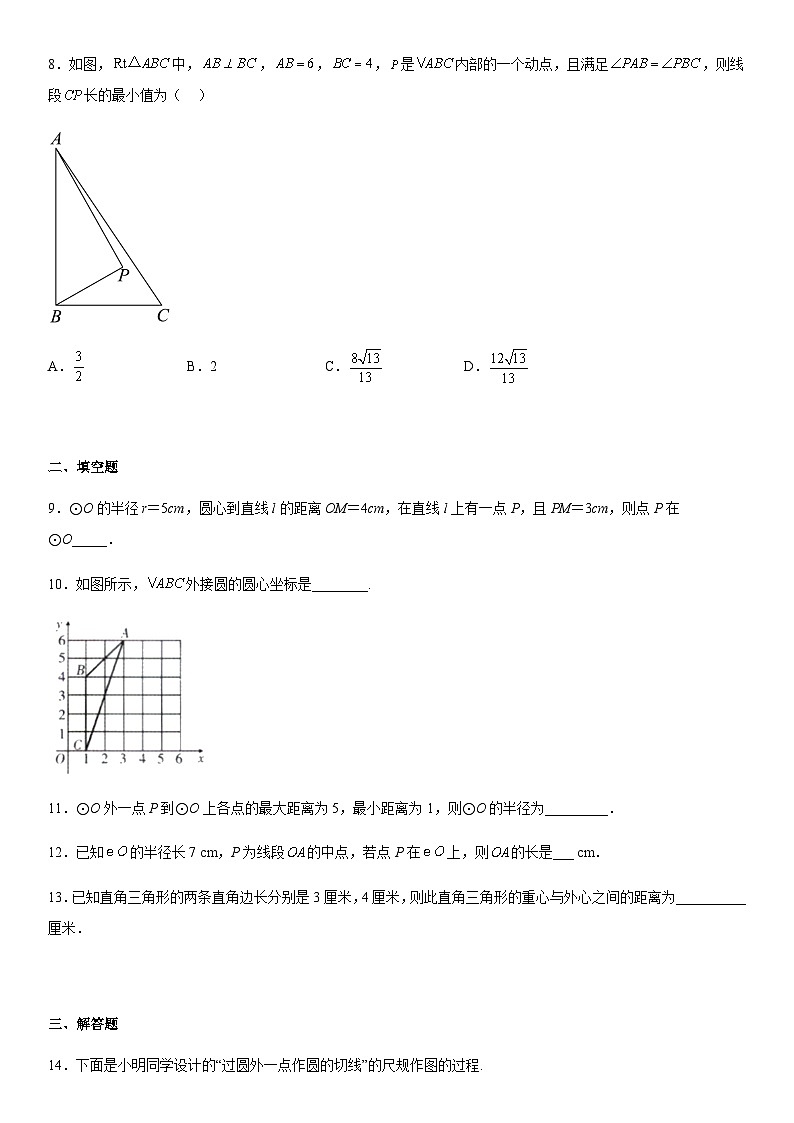
人教版九年级上册数学24.2.1点和圆的位置关系 课时作业一、单选题1．已知⊙O的半径为4cm，点P在⊙O上，则OP的长为（    ）A．1cm B．2cm C．4cm D．8cm2．圆心为O的两个同心圆，半径分别是2和3，若，则点P在（    ）A．大圆上 B．小圆内 C．大圆外 D．大圆内、小圆外3．如图，⊙O的半径为5cm，直线l到点O的距离OM=3cm，点A在l上，AM=3.8cm，则点A与⊙O的位置关系是(     )A．在⊙O内 B．在⊙O上 C．在⊙O外 D．以上都有可能4．下列说法正确的是（    ）A．等弧所对的圆心角相等 B．同弦所对的圆周角相等C．经过三点可以作一个圆 D．相等的圆心角所对的弧相等5．已知⊙O半径为4，圆心O在坐标原点上，点P的坐标为（3，4），则点P与⊙O的位置关系是（　　）A．点P在⊙O内 B．点P在⊙O上 C．点P在⊙O外 D．不能确定6．下列命题正确的是（    ）A．两点之间，射线最短 B．对角线互相垂直平分的四边形是矩形C．正六边形的外角和大于正五边形的外角和 D．不在同一直线上的三个点确定一个圆7．下列四个命题中，正确的有（        ）A．圆的对称轴是直径 B．半径相等的两个半圆是等弧C．三角形的外心到三角形各边的距离相等 D．经过三个点一定可以作圆8．如图，中，，，，是内部的一个动点，且满足，则线段长的最小值为（    ）A． B．2 C． D． 二、填空题9．⊙O的半径r＝5cm，圆心到直线l的距离OM＝4cm，在直线l上有一点P，且PM＝3cm，则点P在⊙O_____．10．如图所示，外接圆的圆心坐标是________.11．⊙O外一点P到⊙O上各点的最大距离为5，最小距离为1，则⊙O的半径为_________．12．已知的半径长7 cm，P为线段的中点，若点P在上，则的长是___ cm．13．已知直角三角形的两条直角边长分别是3厘米，4厘米，则此直角三角形的重心与外心之间的距离为__________厘米． 三、解答题14．下面是小明同学设计的“过圆外一点作圆的切线”的尺规作图的过程.已知：如图1，和外的一点.求作：过点作的切线.作法：如图2，①连接；②作线段的垂直平分线，直线交于；③以点为圆心，为半径作圆，交于点和；④作直线和.则，就是所求作的的切线.根据上述作图过程，回答问题：（1）用直尺和圆规，补全图2中的图形；（2）完成下面的证明：证明：连接，，∵由作图可知是的直径，∴（______）（填依据），∴，，又∵和是的半径，∴，就是的切线（______）（填依据）. 15．求证：等腰三角形的底角必为锐角．       16．七年级教材在图形与几何部分给出了五条基本事实，在《证明》一章中我们从两条基本事实出发，把前面得到的平行线相关性质进行了严格的证明，体会了数学的公里化思想.请完成下列证明活动：活动．利用基本事实证明：“两直线平行，同位角相等”.（在括号内填上相应的基本事实）已知：如图，直线、被直线所截，．求证：．证明：假设，则可以过点作，∵，∴（ ），∴过点存在两条直线、两条直线与平行，这与基本事实（ ）矛盾，∴假设不成立，∴．活动．利用刚刚证明的“两直线平行，同位角相等”证明“两直线平行，同旁内角互补”.（要求画图，写出已知、求证并写出证明过程）已知: ．求证： ．证明：    17．如图，在Rt△ABC中，∠C＝90°，BC＝1，AC＝2，以点B为圆心，BC长为半径画弧交AB于点D；以点A为圆心AD长为半径画弧，交AC于点E，保留作图痕迹，并求的值．