数学八年级下册2.2.1平行四边形的性质练习

[平行四边形的边、角的性质]

一、选择题

1.(2020湘西州凤凰县期末)如图,在▱ABCD中,∠A+∠C=260°,则∠B的度数是 (　　)

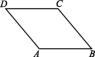
A.110° B.160° C.70° D.50°

2.如图,在平行四边形ABCD中,BE=2,AD=8,DE平分∠ADC交BC于点E,则平行四边形ABCD的周长为              (　　)

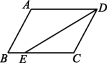
A.14 B.24 C.20 D.28

3.如图,在▱ABCD中,下列结论不一定正确的是 (　　)

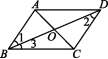
A.∠1=∠2 B.∠1=∠3 C.AB=CD D.∠BAD=∠BCD

4.(2020温州)如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作▱BCDE,则∠E的度数为              (　　)

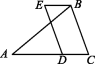
A.40° B.50° C.60° D.70°

二、填空题

5.如图,在▱ABCD中,AE平分∠BAD,过点D作DE⊥AE于点E.若∠ADE=30°,则∠C=　　　　°. 

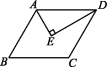
6.如图,E为▱ABCD的边AD上任意一点,▱ABCD的面积为6,则图中阴影部分的面积为　　　　. 

三、解答题

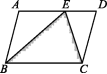
7.如图,在平行四边形ABCD中,E,F分别是边BC,AD的中点.

求证:∠ABF=∠CDE.

图   

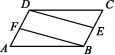
8.(2020重庆B卷)如图,在平行四边形ABCD中,AE,CF分别平分∠BAD和∠DCB,交对角线BD于点E,F.

(1)若∠BCF=60°,求∠ABC的度数;

(2)求证:BE=DF.

图   

9.如图,l1∥l2,点C1在l1上,并且C1A⊥l2,A为垂足,C2,C3是l1上任意两点,点B在l2上.设△ABC1的面积为S1,△ABC2的面积为S2,△ABC3的面积为S3,小颖认为S1=S2=S3,请帮小颖说明理由.

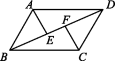
10.如图,在▱ABCD中,∠ABC的平分线交AD于点E,延长BE交CD的延长线于点F.

(1)若∠F=20°,求∠A的度数;

(2)连接CE.若AB=5,BC=8,CE⊥AD,求▱ABCD的面积.

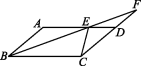
11.如图,在▱ABCD中,∠BCD=120°,分别延长DC,BC到点E,F,使得△BCE和△CDF都是等边三角形,连接AE,FA.

(1)求证:AE=FA;

(2)求∠EAF的度数.

图   

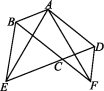
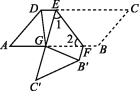
如图,在▱ABCD中,点E,F分别在边DC,AB上,DE=BF,把▱ABCD沿直线EF折叠,使得点B,C分别落在点B',C'处,线段EC'与线段AF交于点G,连接DG,B'G.

求证:(1)∠1=∠2;

(2)DG=B'G.

图   

答案

1. D　∵四边形ABCD是平行四边形,

∴∠A=∠C,∠B+∠C=180°.

又∵∠A+∠C=260°,∴∠C=130°,

∴∠B=180°-130°=50°.

故选D.

2. D　∵DE平分∠ADC,

∴∠ADE=∠CDE.

∵四边形ABCD是平行四边形,

∴AD∥BC,BC=AD=8,AB=CD,

∴∠ADE=∠CED,

∴∠CDE=∠CED,∴CE=CD.

∵BC=8,BE=2,∴CE=BC-BE=8-2=6,∴CD=CE=AB=6,

∴平行四边形ABCD的周长=6+6+8+8=28.

3.B

4. D　由∠A=40°,AB=AC,可得∠C=70°.又因为四边形BCDE是平行四边形,所以∠E=∠C=70°.因此本题选D.

5. 120

 ∵DE⊥AE,∴∠AED=90°,

∴∠EAD+∠ADE=90°.

∵∠ADE=30°,∴∠EAD=60°.

∵AE平分∠BAD,∴∠BAD=120°.

∵四边形ABCD为平行四边形,

∴∠C=∠BAD=120°.

6. 3

 由E是▱ABCD的边AD上任意一点,可得△EBC与▱ABCD等底等高,进而可得S△EBC=S▱ABCD.

7.证明:∵四边形ABCD为平行四边形,

∴AB=CD,AD=BC,∠A=∠C.

∵E,F分别是边BC,AD的中点,

∴CE=BC,AF=AD,

∴AF=CE,

∴△ABF≌△CDE(SAS),

∴∠ABF=∠CDE.

8.解:(1)∵CF平分∠BCD,∴∠BCD=2∠BCF.

∵∠BCF=60°,∴∠BCD=2×60°=120°.

∵四边形ABCD是平行四边形,

∴AB∥CD,∴∠ABC+∠BCD=180°,

∴∠ABC=180°-120°=60°.

(2)证明:∵四边形ABCD是平行四边形,

∴AB=CD,AB∥CD,∠BAD=∠DCB,

∴∠ABE=∠CDF.

∵AE,CF分别平分∠BAD和∠DCB,

∴∠BAE=∠BAD,∠DCF=∠DCB,

∴∠BAE=∠DCF.

在△ABE和△CDF中,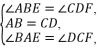

∴△ABE≌△CDF,∴BE=DF.

9.解:如图,分别过点C2,C3作l2的垂线,垂足分别为D,E,则C1A∥C2D∥C3E.

∵l1∥l2,∴C1A=C2D=C3E,

∴△ABC1,△ABC2,△ABC3同底等高,

∴S1=S2=S3.

10.解:(1)∵四边形ABCD是平行四边形,

∴AD∥BC,AB∥CD,

∴∠A+∠ABC=180°,∠ABE=∠F=20°.

∵∠ABC的平分线交AD于点E,

∴∠ABE=∠CBF=20°,

∴∠ABC=40°,∴∠A=140°.

(2)∵四边形ABCD是平行四边形,AB=5,BC=8,

∴AD∥BC,AD=BC=8,CD=AB=5,

∴∠AEB=∠EBC.

∵BE平分∠ABC,∴∠ABE=∠EBC,

∴∠AEB=∠ABE,

∴AE=AB=5,∴DE=AD-AE=3.

∵CE⊥AD,∴∠CED=90°,

∴CE===4,

∴▱ABCD的面积=AD·CE=8×4=32.

11.解:(1)证明:∵四边形ABCD是平行四边形,∠BCD=120°,

∴AB=CD,DA=BC,∠BAD=∠BCD=120°,∠ABC=∠ADC=60°.

∵△BCE和△CDF都是等边三角形,

∴BC=BE,CD=FD,∠EBC=∠CDF=60°,

∴BE=DA,∠ABE=∠FDA=120°,AB=FD,∴△ABE≌△FDA,∴AE=FA.

(2)∵△ABE≌△FDA,∴∠BAE=∠DFA.

∵∠FDA=120°,∴∠DAF+∠DFA=60°,

∴∠DAF+∠BAE=60°,

∴∠EAF=∠BAD-(∠DAF+∠BAE)=60°.

[素养提升]

证明:(1)∵四边形ABCD为平行四边形,

∴AB∥CD,∴∠2=∠FEC.

由折叠的性质,得∠1=∠FEC,

∴∠1=∠2.

(2)由(1)知∠1=∠2,∴EG=FG.

∵AB∥CD,

∴∠DEG=∠EGF.

由折叠的性质,得EC'∥B'F,BF=B'F,

∴∠B'FG=∠EGF,

∴∠B'FG=∠DEG.

∵DE=BF,BF=B'F,

∴DE=B'F,

∴△DEG≌△B'FG,

∴DG=B'G.