

福建省龙岩市北城中学2022-2023学年七年级数学第二学期期末学业水平测试模拟试题含答案
展开
这是一份福建省龙岩市北城中学2022-2023学年七年级数学第二学期期末学业水平测试模拟试题含答案,共7页。试卷主要包含了如图,点A的坐标为等内容,欢迎下载使用。
福建省龙岩市北城中学2022-2023学年七年级数学第二学期期末学业水平测试模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。 一、选择题(每小题3分,共30分)1.对于函数y=-2x+5,下列说法正确的是( )A.图象一定经过(2,-1) B.图象经过一、二、四象限C.图象与直线y=2x+3平行 D.y随x的增大而增大2.菱形的两条对角线长为6 cm 和8 cm,那么这个菱形的周长为A.40 cm B.20 cm C.10 cm D.5 cm3.如图,在△ABC中,DE∥BC,若![]() =
=![]() ,则
,则![]() 的值为( )
的值为( )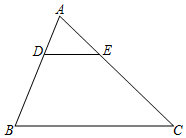 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.在
4.在![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 的对边分别是
的对边分别是![]() 、
、![]() 、
、![]() ,则下列结论错误的是( )A.
,则下列结论错误的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.对于函数y=﹣2x+2,下列结论:①当x>1时,y<0;②它的图象经过第一、二、四象限;③它的图象必经过点(﹣1,2);④y的值随x的增大而增大,其中正确结论的个数是( )A.1 B.2 C.3 D.46.菱形
5.对于函数y=﹣2x+2,下列结论:①当x>1时,y<0;②它的图象经过第一、二、四象限;③它的图象必经过点(﹣1,2);④y的值随x的增大而增大,其中正确结论的个数是( )A.1 B.2 C.3 D.46.菱形![]() 的对角线
的对角线![]() 相交于点
相交于点![]() ,若
,若![]() ,菱形的周长为
,菱形的周长为![]() ,则对角线
,则对角线![]() 的长为( )A.
的长为( )A.![]() B.
B.![]() C.8 D.
C.8 D.![]() 7.下列图案中,既是中心对称又是轴对称的图案是( )A.
7.下列图案中,既是中心对称又是轴对称的图案是( )A. B.
B. C.
C. D.
D. 8.发现下列几组数据能作为三角形的边:(1)8,15,17;(2)5,12,13;(3)12,15,20;(4)7,24,1.其中能作为直角三角形的三边长的有A.1组 B.2组 C.3组 D.4组9.在一次中学生田径运动会上,参加跳远的
8.发现下列几组数据能作为三角形的边:(1)8,15,17;(2)5,12,13;(3)12,15,20;(4)7,24,1.其中能作为直角三角形的三边长的有A.1组 B.2组 C.3组 D.4组9.在一次中学生田径运动会上,参加跳远的![]() 名运动员的成绩如下表所示:成绩(米)
名运动员的成绩如下表所示:成绩(米)![]()
![]()
![]()
![]()
![]()
![]() 人数
人数![]()
![]()
![]()
![]()
![]()
![]() 则这
则这![]() 名运动员成绩的中位数、众数分别是( )A.
名运动员成绩的中位数、众数分别是( )A.![]() B.
B.![]() C.
C.![]() , D.
, D.![]() 10.如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,则点C的纵坐标y与x的函数解析式是( )
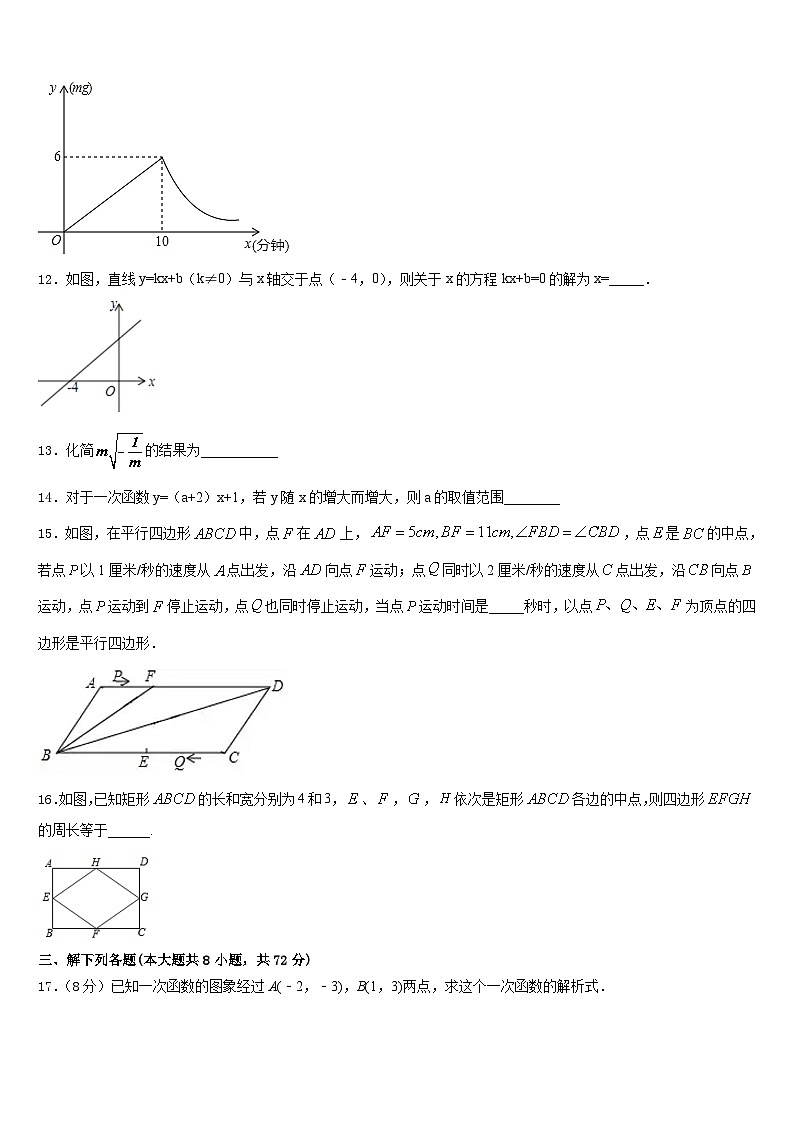
10.如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,则点C的纵坐标y与x的函数解析式是( )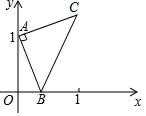 A.y=x B.y=1﹣x C.y=x+1 D.y=x﹣1二、填空题(本大题共有6小题,每小题3分,共18分)11.为预防传染病,某校定期对教室进行“药熏消毒”,已知药物燃烧阶段,室内每立方米空气中的含药量
A.y=x B.y=1﹣x C.y=x+1 D.y=x﹣1二、填空题(本大题共有6小题,每小题3分,共18分)11.为预防传染病,某校定期对教室进行“药熏消毒”,已知药物燃烧阶段,室内每立方米空气中的含药量![]() 与燃烧时间
与燃烧时间![]() (分钟)成正比例;烧灼后,
(分钟)成正比例;烧灼后,![]() 与
与![]() 成反比例(如图所示).现测得药物
成反比例(如图所示).现测得药物![]() 分钟燃烧完,此时教室内每立方米空气含药量为
分钟燃烧完,此时教室内每立方米空气含药量为![]() .研究表明当每立方米空气中含药量低于
.研究表明当每立方米空气中含药量低于![]() 时,对人体方能无毒作用,那么从消毒开始,至少需要经过______分钟后,学生才能回到教室.
时,对人体方能无毒作用,那么从消毒开始,至少需要经过______分钟后,学生才能回到教室.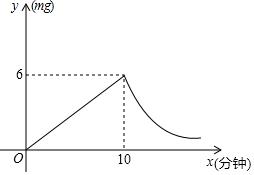 12.如图,直线y=kx+b(k≠0)与x轴交于点(﹣4,0),则关于x的方程kx+b=0的解为x=_____.
12.如图,直线y=kx+b(k≠0)与x轴交于点(﹣4,0),则关于x的方程kx+b=0的解为x=_____.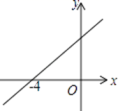 13.化简
13.化简![]() 的结果为___________14.对于一次函数y=(a+2)x+1,若y随x的增大而增大,则a的取值范围________15.如图,在平行四边形
的结果为___________14.对于一次函数y=(a+2)x+1,若y随x的增大而增大,则a的取值范围________15.如图,在平行四边形![]() 中,点
中,点![]() 在
在![]() 上,
上,![]() ,点
,点![]() 是
是![]() 的中点,若点
的中点,若点![]() 以1厘米/秒的速度从
以1厘米/秒的速度从![]() 点出发,沿
点出发,沿![]() 向点
向点![]() 运动;点
运动;点![]() 同时以2厘米/秒的速度从
同时以2厘米/秒的速度从![]() 点出发,沿
点出发,沿![]() 向点
向点![]() 运动,点
运动,点![]() 运动到
运动到![]() 停止运动,点
停止运动,点![]() 也同时停止运动,当点
也同时停止运动,当点![]() 运动时间是_____秒时,以点
运动时间是_____秒时,以点![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.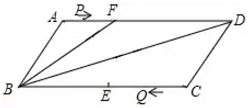 16.如图,已知矩形
16.如图,已知矩形![]() 的长和宽分别为4和3,
的长和宽分别为4和3,![]() 、
、![]() ,
,![]() ,
,![]() 依次是矩形
依次是矩形![]() 各边的中点,则四边形
各边的中点,则四边形![]() 的周长等于______.
的周长等于______.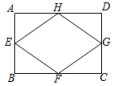 三、解下列各题(本大题共8小题,共72分)17.(8分)已知一次函数的图象经过A(﹣2,﹣3),B(1,3)两点,求这个一次函数的解析式. 18.(8分)哈市某专卖店销售某品牌服装,设服装进价为80元,当每件服装售价为240元时,月销售为200件,该专卖店为提高经营利润,准备采取降价的方式进行促销,经市场调查发现:当每件价格每下降10元时,月销售量就会增加20件,设每件服装售价为x(元),该专卖店的月利润为y(元).
三、解下列各题(本大题共8小题,共72分)17.(8分)已知一次函数的图象经过A(﹣2,﹣3),B(1,3)两点,求这个一次函数的解析式. 18.(8分)哈市某专卖店销售某品牌服装,设服装进价为80元,当每件服装售价为240元时,月销售为200件,该专卖店为提高经营利润,准备采取降价的方式进行促销,经市场调查发现:当每件价格每下降10元时,月销售量就会增加20件,设每件服装售价为x(元),该专卖店的月利润为y(元).
(1)求出y与x的函数关系式(不要求写出x的取值范围);
(2)该专卖店要获得最大月利润,售价应定为每件多少元?最大利润是多少? 19.(8分)心理学家研究发现,一般情况下,一节课![]() 分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为 理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数
分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为 理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数![]() 随时间
随时间![]() (分钟)的变化规律如图所示(其中
(分钟)的变化规律如图所示(其中![]() 都为线段)
都为线段)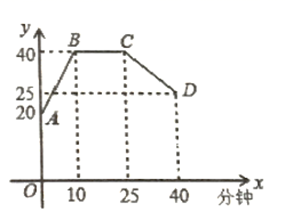 (1)分别求出线段
(1)分别求出线段![]() 和
和![]() 的函数解析式;(2)开始上课后第
的函数解析式;(2)开始上课后第![]() 分钟时与第
分钟时与第![]() 分钟时相比较,何时学生的注意力更集中?(3)一道数学竞赛题,需要讲
分钟时相比较,何时学生的注意力更集中?(3)一道数学竞赛题,需要讲![]() 分钟,为了效果较好,要求学生的注意力指标数最低达到
分钟,为了效果较好,要求学生的注意力指标数最低达到![]() 那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目? 20.(8分)如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在y轴上运动.(1)求直线AB的函数解析式;(2)动点M在y轴上运动,使MA+MB的值最小,求点M的坐标;(3)在y轴的负半轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.
那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目? 20.(8分)如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在y轴上运动.(1)求直线AB的函数解析式;(2)动点M在y轴上运动,使MA+MB的值最小,求点M的坐标;(3)在y轴的负半轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.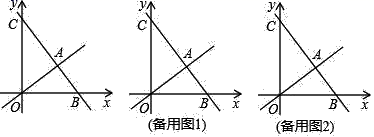 21.(8分)某公司招聘人才,对应聘者分别进行了阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的测试成绩(百分制)如下表:(单位:分)应聘者阅读能力思维能力表达能力甲859080乙958095(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将被录用?(2)若将阅读能力、思维能力和表达能力三项测试得分按1:3:1的比确定每人的最后成绩,谁将被录用? 22.(10分)如图1,正方形ABCD中,AB=4cm,点P从点D出发沿DA向点A匀速运动,速度是1cm/s,同时,点Q从点A出发沿AB方向,向点B匀速运动,速度是2cm/s,连接PQ、CP、CQ,设运动时间为t(s)(0<t<2)(1)是否存在某一时刻t,使得PQ∥BD?若存在,求出t值;若不存在,说明理由(2)设△PQC的面积为s(cm2),求s与t之间的函数关系式;(3)如图2,连接AC,与线段PQ相交于点M,是否存在某一时刻t,使S△QCM:S△PCM=3:5?若存在,求出t值;若不存在,说明理由.
21.(8分)某公司招聘人才,对应聘者分别进行了阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的测试成绩(百分制)如下表:(单位:分)应聘者阅读能力思维能力表达能力甲859080乙958095(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将被录用?(2)若将阅读能力、思维能力和表达能力三项测试得分按1:3:1的比确定每人的最后成绩,谁将被录用? 22.(10分)如图1,正方形ABCD中,AB=4cm,点P从点D出发沿DA向点A匀速运动,速度是1cm/s,同时,点Q从点A出发沿AB方向,向点B匀速运动,速度是2cm/s,连接PQ、CP、CQ,设运动时间为t(s)(0<t<2)(1)是否存在某一时刻t,使得PQ∥BD?若存在,求出t值;若不存在,说明理由(2)设△PQC的面积为s(cm2),求s与t之间的函数关系式;(3)如图2,连接AC,与线段PQ相交于点M,是否存在某一时刻t,使S△QCM:S△PCM=3:5?若存在,求出t值;若不存在,说明理由.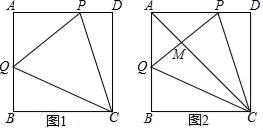 23.(10分)某工厂制作甲、乙两种窗户边框,已知同样用12米材料制成甲种边框的个数比制成乙种边框的个数少1个,且制成一个甲种边框比制成一个乙种边框需要多用
23.(10分)某工厂制作甲、乙两种窗户边框,已知同样用12米材料制成甲种边框的个数比制成乙种边框的个数少1个,且制成一个甲种边框比制成一个乙种边框需要多用![]() 的材料.(1)求制作每个甲种边框、乙种边框各用多少米材料?(2)如果制作甲、乙两种边框的材料共640米,要求制作乙种边框的数量不少于甲种边框数量的2倍,求应最多安排制作甲种边框多少个(不计材料损耗)? 24.(12分)为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了“汉子听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉子得1分,本次决赛,学生成绩为x(分),且
的材料.(1)求制作每个甲种边框、乙种边框各用多少米材料?(2)如果制作甲、乙两种边框的材料共640米,要求制作乙种边框的数量不少于甲种边框数量的2倍,求应最多安排制作甲种边框多少个(不计材料损耗)? 24.(12分)为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了“汉子听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉子得1分,本次决赛,学生成绩为x(分),且![]() (无满分),将其按分数段分为五组,绘制出以下不完整表格:
(无满分),将其按分数段分为五组,绘制出以下不完整表格: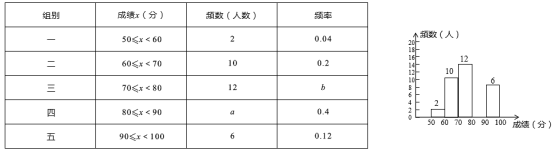 请根据表格提供的信息,解答以下问题:(1)本次决赛共有________名学生参加;(2)直接写出表中:a= ,b= 。(3)请补全右面相应的频数分布直方图;(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为________. 参考答案 一、选择题(每小题3分,共30分)1、B2、B3、D4、D5、B6、C7、D8、C9、D10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、112、-113、
请根据表格提供的信息,解答以下问题:(1)本次决赛共有________名学生参加;(2)直接写出表中:a= ,b= 。(3)请补全右面相应的频数分布直方图;(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为________. 参考答案 一、选择题(每小题3分,共30分)1、B2、B3、D4、D5、B6、C7、D8、C9、D10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、112、-113、![]() 14、a>-115、3或
14、a>-115、3或![]() 16、1 三、解下列各题(本大题共8小题,共72分)17、y=2x+118、(1)y=−2x2+840x−54400;(2)售价应定为每件210元,最大利润是33800元.19、(1)线段AB的解析式为:y1=2x+1;线段CD的解析式为:
16、1 三、解下列各题(本大题共8小题,共72分)17、y=2x+118、(1)y=−2x2+840x−54400;(2)售价应定为每件210元,最大利润是33800元.19、(1)线段AB的解析式为:y1=2x+1;线段CD的解析式为:![]() ;(2)第30分钟注意力更集中;(3)能.20、(1)y=-x+6;(2)M(0,
;(2)第30分钟注意力更集中;(3)能.20、(1)y=-x+6;(2)M(0,![]() );(3)(0,-2)或(0,-6).21、(1)乙将被录用;(2)甲将被录用22、(1)
);(3)(0,-2)或(0,-6).21、(1)乙将被录用;(2)甲将被录用22、(1)![]() ;(2)S=t2﹣2t+8(0<t<2);(3)
;(2)S=t2﹣2t+8(0<t<2);(3)![]() . 23、(1)甲框每个2.4米,乙框每个2米;(2)最多可购买甲种边框100个.24、(1)50;(2)20,0.24;(3)详见解析;(4)52%.
. 23、(1)甲框每个2.4米,乙框每个2米;(2)最多可购买甲种边框100个.24、(1)50;(2)20,0.24;(3)详见解析;(4)52%.
相关试卷
这是一份福建省龙岩市北城中学2023-2024学年数学九上期末学业质量监测试题含答案,共8页。试卷主要包含了考生要认真填写考场号和座位序号,当压力F,一元二次方程的常数项是等内容,欢迎下载使用。
这是一份2023-2024学年福建省龙岩市北城中学数学九上期末监测模拟试题含答案,共9页。试卷主要包含了方程的根是等内容,欢迎下载使用。
这是一份山东省单县北城第三初级中学2022-2023学年七下数学期末学业水平测试试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,如果一次函数y=kx+b等内容,欢迎下载使用。








