

安徽省含山县2022-2023学年数学七年级第二学期期末预测试题含答案
展开
这是一份安徽省含山县2022-2023学年数学七年级第二学期期末预测试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,正方形的一个内角度数是,点关于轴对称的点的坐标是,下列说法等内容,欢迎下载使用。
安徽省含山县2022-2023学年数学七年级第二学期期末预测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1.如图,正方形![]() 的对角线
的对角线![]() 是菱形
是菱形![]() 的一边,则
的一边,则![]() 等于( )
等于( )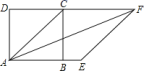 A.135° B.45° C.22.5° D.30°2.用反证法证明“三角形的三个外角中至多有一个锐角”,应先假设
A.135° B.45° C.22.5° D.30°2.用反证法证明“三角形的三个外角中至多有一个锐角”,应先假设![]()
![]() A.三角形的三个外角都是锐角B.三角形的三个外角中至少有两个锐角C.三角形的三个外角中没有锐角D.三角形的三个外角中至少有一个锐角3.将直线
A.三角形的三个外角都是锐角B.三角形的三个外角中至少有两个锐角C.三角形的三个外角中没有锐角D.三角形的三个外角中至少有一个锐角3.将直线![]() 向下平移
向下平移![]() 个单位后所得直线的解析式为( )A.
个单位后所得直线的解析式为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.在直角坐标系中,点
4.在直角坐标系中,点![]() 关于原点对称的点为
关于原点对称的点为![]() ,则点
,则点![]() 的坐标是( )A.
的坐标是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.正方形的一个内角度数是
5.正方形的一个内角度数是![]()
![]() A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6.利用函数
6.利用函数![]() 的图象解得
的图象解得![]() 的解集是
的解集是![]() ,则
,则![]() 的图象是( )A.
的图象是( )A.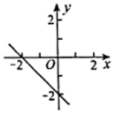 B.
B.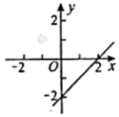 C.
C.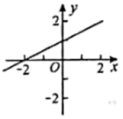 D.
D.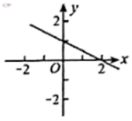 7.点
7.点![]() 关于
关于![]() 轴对称的点的坐标是( )A.
轴对称的点的坐标是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 8.若分式
8.若分式![]() 有意义,则 x 的取值范围是( )A.x >3 B.x <3 C.x =3 D.x ≠39.在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为( )A.9人 B.10人 C.11人 D.12人10.下列说法:①对角线互相垂直的四边形是菱形;②矩形的对角线垂直且互相平分;③对角线相等的四边形是矩形;④对角线相等的菱形是正方形;⑤邻边相等的矩形是正方形.其中正确的是( )A.
有意义,则 x 的取值范围是( )A.x >3 B.x <3 C.x =3 D.x ≠39.在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为( )A.9人 B.10人 C.11人 D.12人10.下列说法:①对角线互相垂直的四边形是菱形;②矩形的对角线垂直且互相平分;③对角线相等的四边形是矩形;④对角线相等的菱形是正方形;⑤邻边相等的矩形是正方形.其中正确的是( )A.![]() 个 B.
个 B.![]() 个 C.
个 C.![]() 个 D.
个 D.![]() 个二、填空题(本大题共有6小题,每小题3分,共18分)11.已知一组数据6,x,3,3,5,1的众数是3和5,则这组数据的中位数是_____.12.解分式方程
个二、填空题(本大题共有6小题,每小题3分,共18分)11.已知一组数据6,x,3,3,5,1的众数是3和5,则这组数据的中位数是_____.12.解分式方程![]() +
+![]() =
=![]() 时,设
时,设![]() =y,则原方程化为关于y的整式方程是______.13.某初中校女子排球队队员的年龄分布:年龄/(岁)13141516频数1452该校女子排球队队员的平均年龄是_____岁.(结果精确到0.1)14.如图,已知直线y=
=y,则原方程化为关于y的整式方程是______.13.某初中校女子排球队队员的年龄分布:年龄/(岁)13141516频数1452该校女子排球队队员的平均年龄是_____岁.(结果精确到0.1)14.如图,已知直线y=![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点,且点A的横坐标为
的图象交于A,B两点,且点A的横坐标为![]() .在坐标轴上找一点C,直线AB上找一点D,在双曲线y=
.在坐标轴上找一点C,直线AB上找一点D,在双曲线y=![]() 找一点E,若以O,C,D,E为顶点的四边形是有一组对角为60∘的菱形,那么符合条件点D的坐标为___.
找一点E,若以O,C,D,E为顶点的四边形是有一组对角为60∘的菱形,那么符合条件点D的坐标为___.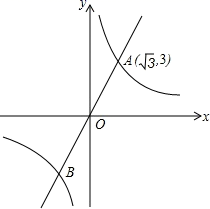 15.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C/处,BC/交AD于E,AD=8,AB=4,DE的长=________________.
15.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C/处,BC/交AD于E,AD=8,AB=4,DE的长=________________. 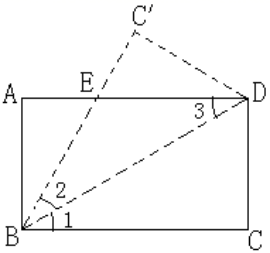 16.已知一个直角三角形的斜边长为6cm,那么这个直角三角形斜边上的中线长为________cm.三、解下列各题(本大题共8小题,共72分)17.(8分)如图,在
16.已知一个直角三角形的斜边长为6cm,那么这个直角三角形斜边上的中线长为________cm.三、解下列各题(本大题共8小题,共72分)17.(8分)如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 的垂直平分线分别交
的垂直平分线分别交![]() 和
和![]() 于点
于点![]() 、
、![]() .求证:
.求证:![]() .
.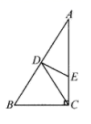 18.(8分)如图,已知
18.(8分)如图,已知![]() ABC,利用尺规在AC边上求作点D,使AD=BD(保留作图痕迹,不写作法)
ABC,利用尺规在AC边上求作点D,使AD=BD(保留作图痕迹,不写作法) 19.(8分)小明和爸爸周末到湿地公园进行锻炼,两人同时从家出发,匀速骑共享单车到达公园入口,然后一同匀速步行到达驿站,到达驿站后小明的爸爸立即又骑共享单车按照来时骑行速度原路返回,在公园入口处改为步行,并按来时步行速度原路回家,小明到达驿站后逗留了10分钟之后骑车回家,爸爸在锻炼过程中离出发地的路程与出发的时间的函数关系如图.(1)图中m=_____,n=_____;(直接写出结果)(2)小明若要在爸爸到家之前赶上,问小明回家骑行速度至少是多少?
19.(8分)小明和爸爸周末到湿地公园进行锻炼,两人同时从家出发,匀速骑共享单车到达公园入口,然后一同匀速步行到达驿站,到达驿站后小明的爸爸立即又骑共享单车按照来时骑行速度原路返回,在公园入口处改为步行,并按来时步行速度原路回家,小明到达驿站后逗留了10分钟之后骑车回家,爸爸在锻炼过程中离出发地的路程与出发的时间的函数关系如图.(1)图中m=_____,n=_____;(直接写出结果)(2)小明若要在爸爸到家之前赶上,问小明回家骑行速度至少是多少?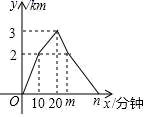 20.(8分)如图,在平面直角坐标系中,点A(1,4),点B(3,2),连接OA,OB.
20.(8分)如图,在平面直角坐标系中,点A(1,4),点B(3,2),连接OA,OB.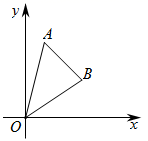 (1)求直线OB与AB的解析式;(2)求△AOB的面积.(3)下面两道小题,任选一道作答.作答时,请注明题号,若多做,则按首做题计入总分.①在y轴上是否存在一点P,使△PAB周长最小.若存在,请直接写出点P坐标;若不存在,请说明理由.②在平面内是否存在一点C,使以A,O,C,B为顶点的四边形是平行四边形.若存在,请直接写出点C坐标;若不存在,请说明理由. 21.(8分)如图,已知函数
(1)求直线OB与AB的解析式;(2)求△AOB的面积.(3)下面两道小题,任选一道作答.作答时,请注明题号,若多做,则按首做题计入总分.①在y轴上是否存在一点P,使△PAB周长最小.若存在,请直接写出点P坐标;若不存在,请说明理由.②在平面内是否存在一点C,使以A,O,C,B为顶点的四边形是平行四边形.若存在,请直接写出点C坐标;若不存在,请说明理由. 21.(8分)如图,已知函数![]() 和
和![]() 的图象交于点
的图象交于点![]() ,这两个函数的图象与
,这两个函数的图象与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() .
.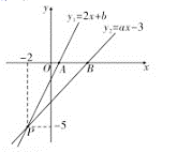 (1)分别求出这两个函数的解析式;(2)求
(1)分别求出这两个函数的解析式;(2)求![]() 的面积;(3)根据图象直接写出
的面积;(3)根据图象直接写出![]() 时,
时,![]() 的取值范围. 22.(10分)定义:如图(1),
的取值范围. 22.(10分)定义:如图(1),![]() ,
,![]() ,
,![]() ,
,![]() 四点分别在四边形
四点分别在四边形![]() 的四条边上,若四边形
的四条边上,若四边形![]() 为菱形,我们称菱形
为菱形,我们称菱形![]() 为四边形
为四边形![]() 的内接菱形.动手操作:
的内接菱形.动手操作:
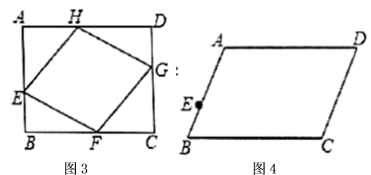 (1)如图2,网格中的每个小四边形都为正方形,每个小四边形的顶点叫做格点,由
(1)如图2,网格中的每个小四边形都为正方形,每个小四边形的顶点叫做格点,由![]() 个小正方形组成一个大正方形
个小正方形组成一个大正方形![]() ,点
,点![]() 、
、![]() 在格点上,请在图(2)中画出四边形
在格点上,请在图(2)中画出四边形![]() 的内接菱形
的内接菱形![]() ;特例探索:(2)如图3,矩形
;特例探索:(2)如图3,矩形![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上且
上且![]() ,四边形
,四边形![]() 是矩形
是矩形![]() 的内接菱形,求
的内接菱形,求![]() 的长度;拓展应用:(3)如图4,平行四边形
的长度;拓展应用:(3)如图4,平行四边形![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上且
上且![]() ,①请你在图4中画出平行四边形
,①请你在图4中画出平行四边形![]() 的内接菱形
的内接菱形![]() ,点
,点![]() 在边
在边![]() 上;②在①的条件下,当
上;②在①的条件下,当![]() 的长最短时,
的长最短时,![]() 的长为__________ 23.(10分)计算:5
的长为__________ 23.(10分)计算:5![]() ÷
÷![]() ﹣3
﹣3![]() +2
+2![]() . 24.(12分)已知:如图,在▱ABCD中,延长AB到点E.使BE=AB,连接DE交BC于点F.求证:△BEF≌△CDF.
. 24.(12分)已知:如图,在▱ABCD中,延长AB到点E.使BE=AB,连接DE交BC于点F.求证:△BEF≌△CDF.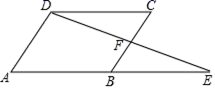 参考答案 一、选择题(每小题3分,共30分)1、C2、B3、D4、B5、D6、C7、A8、D9、C10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、112、y2-
参考答案 一、选择题(每小题3分,共30分)1、C2、B3、D4、B5、D6、C7、A8、D9、C10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、112、y2-![]() y+1=113、14.1.14、 (3,3
y+1=113、14.1.14、 (3,3![]() )或(−3,−3
)或(−3,−3![]() ).15、516、1 三、解下列各题(本大题共8小题,共72分)17、详见解析18、见解析19、 (1)25,1;(2)小明回家骑行速度至少是0.2千米/分.20、(1)直线OB的解析式为
).15、516、1 三、解下列各题(本大题共8小题,共72分)17、详见解析18、见解析19、 (1)25,1;(2)小明回家骑行速度至少是0.2千米/分.20、(1)直线OB的解析式为![]() ,直线AB的解析式为y= -x+1(2)1;(3)①存在,(0,
,直线AB的解析式为y= -x+1(2)1;(3)①存在,(0,![]() );②存在,(2,-2)或(4,6)或(-2,2)21、 (1)
);②存在,(2,-2)或(4,6)或(-2,2)21、 (1)![]() ,
,![]() ;(2)S△ABC=
;(2)S△ABC=![]() ;(3)
;(3)![]() 时,
时,![]() .22、(1)详见解析;(2)3;(3)①详见解析;②
.22、(1)详见解析;(2)3;(3)①详见解析;②![]() 的长为
的长为![]() 23、8
23、8![]() 24、可证明∠CDF=∠B,BE=CD,∠C=∠FBE∴△BEF≌△CDF(ASA)
24、可证明∠CDF=∠B,BE=CD,∠C=∠FBE∴△BEF≌△CDF(ASA)
相关试卷
这是一份安徽省含山县2023-2024学年八上数学期末达标检测试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,以下命题的逆命题为真命题的是,计算,得等内容,欢迎下载使用。
这是一份安徽省滁州市琅琊区2022-2023学年数学七年级第二学期期末预测试题含答案,共7页。
这是一份安徽省合肥庐江县联考2022-2023学年七年级数学第二学期期末预测试题含答案,共8页。试卷主要包含了通过估算,估计的大小应在,若a≤1,则化简后为等内容,欢迎下载使用。








