

安徽省合肥市巢湖市2022-2023学年数学七下期末联考模拟试题含答案
展开
这是一份安徽省合肥市巢湖市2022-2023学年数学七下期末联考模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列各式中属于最简二次根式的是,若,则的值,方程x2 = 2x的解是等内容,欢迎下载使用。
安徽省合肥市巢湖市2022-2023学年数学七下期末联考模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.方程x(x﹣1)=0的根是( )A.x=0 B.x=1 C.x1=0,x2=1 D.x1=0,x2=﹣12.某社区超市以4元/瓶从厂家购进一批饮料,以6元/瓶销售.近期计划进行打折销售,若这批饮料的销售利润不低于20%则最多可以打( ) A.六折 B.七折 C.七五折 D.八折3.函数
A.六折 B.七折 C.七五折 D.八折3.函数 ![]() 中,自变量
中,自变量 ![]() 的取值范围是( )A.
的取值范围是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心以相同的长(大于
4.如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心以相同的长(大于![]() AB)为半径作弧,两弧相交于点M和N点,作直线MN交AB于点D,交BC于点E,若AC=3,BC=4,则BE等于( )
AB)为半径作弧,两弧相交于点M和N点,作直线MN交AB于点D,交BC于点E,若AC=3,BC=4,则BE等于( )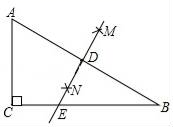 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.为了了解2013年昆明市九年级学生学业水平考试的数学成绩,从中随机抽取了1000名学生的数学成绩.下列说法正确的是( )A.2013年昆明市九年级学生是总体 B.每一名九年级学生是个体C.1000名九年级学生是总体的一个样本 D.样本容量是10006.下列各式中属于最简二次根式的是( ).A.
5.为了了解2013年昆明市九年级学生学业水平考试的数学成绩,从中随机抽取了1000名学生的数学成绩.下列说法正确的是( )A.2013年昆明市九年级学生是总体 B.每一名九年级学生是个体C.1000名九年级学生是总体的一个样本 D.样本容量是10006.下列各式中属于最简二次根式的是( ).A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.若
7.若![]() ,则
,则![]() 的值( )A.
的值( )A.![]() B.
B.![]() C.–7 D.78.如图,直线
C.–7 D.78.如图,直线![]() ,直线
,直线![]() 分别交直线
分别交直线![]() 、
、![]() 、
、![]() 于点
于点![]() 、
、![]() 、
、![]() ,直线
,直线![]() 分別交直线
分別交直线![]() ,
,![]() 、
、![]() 于点
于点![]() 、
、![]() 、
、![]() ,直线
,直线![]() 、
、![]() 交于点
交于点![]() ,则下列结论错误的是( )
,则下列结论错误的是( )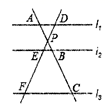 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.一个正多边形的内角和是1440°,则它的每个外角的度数是( )A.30° B.36° C.45° D.60°10.方程x2 = 2x的解是( )A.x=2 B.x1=
9.一个正多边形的内角和是1440°,则它的每个外角的度数是( )A.30° B.36° C.45° D.60°10.方程x2 = 2x的解是( )A.x=2 B.x1=![]() ,x2= 0 C.x1=2,x2=0 D.x = 011.为了解某小区居民的日用电情况,居住在该小区的一名同学随机抽查了15户居民的日用电量,结果如下表:日用电量(单位:度)45678户数25431则关于这15户家庭的日用电量,下列说法错误的是( )A.众数是5度 B.平均数6度C.极差(最大值-最小值)是4度 D.中位数是6度12.如图,正方形
,x2= 0 C.x1=2,x2=0 D.x = 011.为了解某小区居民的日用电情况,居住在该小区的一名同学随机抽查了15户居民的日用电量,结果如下表:日用电量(单位:度)45678户数25431则关于这15户家庭的日用电量,下列说法错误的是( )A.众数是5度 B.平均数6度C.极差(最大值-最小值)是4度 D.中位数是6度12.如图,正方形![]() 的边长为3,将正方形折叠,使点
的边长为3,将正方形折叠,使点![]() 落在边
落在边![]() 上的点
上的点![]() 处,点
处,点![]() 落在点
落在点![]() 处, 折痕为
处, 折痕为![]() 。若
。若![]() ,则
,则![]() 的长是
的长是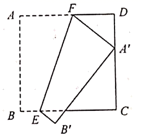 A.1 B.
A.1 B.![]() C.
C.![]() D.2二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别为1,5,1,1.则最大的正方形E的面积是___.
D.2二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别为1,5,1,1.则最大的正方形E的面积是___. 14.若ab=﹣2,a+b=1,则代数式a2b+ab2的值等于_____.15.如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT的长为_____.
14.若ab=﹣2,a+b=1,则代数式a2b+ab2的值等于_____.15.如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT的长为_____.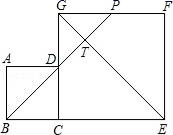 16.若
16.若![]() ,则a与b的大小关系为a_____b(填“>”、“<”或“=”)17.如图,E是正方形ABCD的对角线BD上任意一点,四边形EGCG是矩形,若正方形ABCD的周长为a,则矩形EFCG的周长为_______________.
,则a与b的大小关系为a_____b(填“>”、“<”或“=”)17.如图,E是正方形ABCD的对角线BD上任意一点,四边形EGCG是矩形,若正方形ABCD的周长为a,则矩形EFCG的周长为_______________.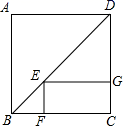 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图1,已知正方形ABCD的边长为6,E是CD边上一点(不与点C 重合),以CE为边在正方形ABCD的右侧作正方形CEFG,连接BF、BD、FD.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图1,已知正方形ABCD的边长为6,E是CD边上一点(不与点C 重合),以CE为边在正方形ABCD的右侧作正方形CEFG,连接BF、BD、FD. 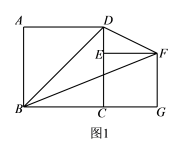
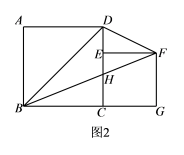 (1)当点E与点D重合时,△BDF的面积为 ;当点E为CD的中点时,△BDF的面积为 .(2)当E是CD边上任意一点(不与点C重合)时,猜想S△BDF与S正方形ABCD之间的关系,并证明你的猜想; (3)如图2,设BF与CD相交于点H,若△DFH的面积为
(1)当点E与点D重合时,△BDF的面积为 ;当点E为CD的中点时,△BDF的面积为 .(2)当E是CD边上任意一点(不与点C重合)时,猜想S△BDF与S正方形ABCD之间的关系,并证明你的猜想; (3)如图2,设BF与CD相交于点H,若△DFH的面积为![]() ,求正方形CEFG的边长. 19.(5分)在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).(1)当﹣2<x≤3时,求y的取值范围;(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标. 20.(8分)已知y与x+2 成正比例,当x=4时,y=12.(1)写出y与x之间的函数解析式;(2)求当y=36时x的值;(3)判断点(-7,-10)是否是函数图象上的点. 21.(10分)为增强学生的身体素质,教育行政部门规定每位学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:(1)在这次调查中共调查了多少名学生?(2)求户外活动时间为1.5小时的人数,并补充频数分布直方图;(3)户外活动时间的众数和中位数分别是多少?(4)若该市共有20000名学生,大约有多少学生户外活动的平均时间符合要求?
,求正方形CEFG的边长. 19.(5分)在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).(1)当﹣2<x≤3时,求y的取值范围;(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标. 20.(8分)已知y与x+2 成正比例,当x=4时,y=12.(1)写出y与x之间的函数解析式;(2)求当y=36时x的值;(3)判断点(-7,-10)是否是函数图象上的点. 21.(10分)为增强学生的身体素质,教育行政部门规定每位学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:(1)在这次调查中共调查了多少名学生?(2)求户外活动时间为1.5小时的人数,并补充频数分布直方图;(3)户外活动时间的众数和中位数分别是多少?(4)若该市共有20000名学生,大约有多少学生户外活动的平均时间符合要求?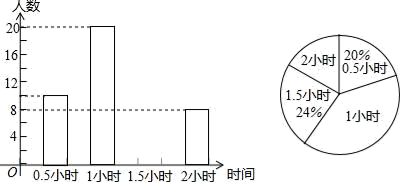 22.(10分)如图,在平面直角坐标系
22.(10分)如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的顶点
的顶点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 边上从点
边上从点![]() 运动到点
运动到点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,连
,连![]() ,在点
,在点![]() 运动过程中,请探究以下问题:
运动过程中,请探究以下问题: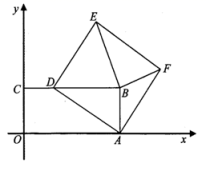 (1)
(1)![]() 的面积是否改变,如果不变,求出该定值;如果改变,请说明理由;(2)若
的面积是否改变,如果不变,求出该定值;如果改变,请说明理由;(2)若![]() 为等腰三角形,求此时正方形
为等腰三角形,求此时正方形![]() 的边长. 23.(12分)如图,在△ABC中,∠ACB=90°,AC=30cm,BC=40cm.点P从点A出发,以5cm/s的速度沿AC向终点C匀速移动.过点P作PQ⊥AB,垂足为点Q,以PQ为边作正方形PQMN,点M在AB边上,连接CN.设点P移动的时间为t(s).
的边长. 23.(12分)如图,在△ABC中,∠ACB=90°,AC=30cm,BC=40cm.点P从点A出发,以5cm/s的速度沿AC向终点C匀速移动.过点P作PQ⊥AB,垂足为点Q,以PQ为边作正方形PQMN,点M在AB边上,连接CN.设点P移动的时间为t(s).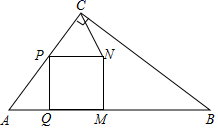 (1)PQ=______;(用含t的代数式表示)(2)当点N分别满足下列条件时,求出相应的t的值;①点C,N,M在同一条直线上;②点N落在BC边上;(3)当△PCN为等腰三角形时,求t的值. 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、D3、D4、D5、D6、B7、D8、C9、B10、C11、B12、B 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、214、﹣115、2
(1)PQ=______;(用含t的代数式表示)(2)当点N分别满足下列条件时,求出相应的t的值;①点C,N,M在同一条直线上;②点N落在BC边上;(3)当△PCN为等腰三角形时,求t的值. 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、D3、D4、D5、D6、B7、D8、C9、B10、C11、B12、B 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、214、﹣115、2 ![]() 16、=17、
16、=17、![]() 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)1,1;(2)S△BDF=
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)1,1;(2)S△BDF=![]() S正方形ABCD,证明见解析;(3)219、 (1) ﹣4≤y<1;(2)点P的坐标为(2,﹣2) .20、 (1)y=2(x+2)=2x+4;(2)x=16;(3)点(-7,-10)是函数图象上的点.21、 (1)50;(2)12;(3)中数是1小时,中位数是1小时;(4)16000人.22、(1)不变,
S正方形ABCD,证明见解析;(3)219、 (1) ﹣4≤y<1;(2)点P的坐标为(2,﹣2) .20、 (1)y=2(x+2)=2x+4;(2)x=16;(3)点(-7,-10)是函数图象上的点.21、 (1)50;(2)12;(3)中数是1小时,中位数是1小时;(4)16000人.22、(1)不变,![]() ;(2)正方形ADEF的边长为
;(2)正方形ADEF的边长为![]() 或
或![]() 或
或![]() .23、(1)4t;(2)①
.23、(1)4t;(2)①![]() ,②
,②![]() ;(3)
;(3)![]() 秒或
秒或![]() 秒或
秒或![]() 秒.
秒.
相关试卷
这是一份安徽省十校联考2022-2023学年七下数学期末联考模拟试题含答案,共6页。
这是一份安徽省合肥市名校联考2022-2023学年七下数学期末经典试题含答案,共5页。试卷主要包含了考生要认真填写考场号和座位序号,下列等式中,不成立的是等内容,欢迎下载使用。
这是一份安徽省合肥市庐阳区2022-2023学年数学七下期末监测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。








