


所属成套资源:【单元测试】冀教版初中数学七年级上册 单元检测卷(含答案)
冀教新版七年级上册数学《第2章几何图形的初步认识》单元测试卷(有答案) (2)
展开
这是一份冀教新版七年级上册数学《第2章几何图形的初步认识》单元测试卷(有答案) (2),共12页。试卷主要包含了下列说法不正确的是,下列各直线的表示法中,正确的是等内容,欢迎下载使用。
冀教新版七年级上册数学《第2章 几何图形的初步认识》单元测试卷一.选择题1.如图,在长方体ABCD﹣EFGH中,与面BDHF垂直的平面个数为( )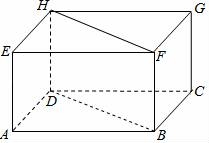 A.1 B.2 C.3 D.42.下列说法不正确的是( )A.长方体与正方体都有六个面 B.圆锥的底面是圆 C.棱柱的上下底面是完全相同的图形 D.五棱柱有五个面,五条棱3.如图,建筑工人砌墙时,经常用细绳在墙的两端之间拉一条参照线,使砌的每一层砖在一条直线上,这样做蕴含的数学原理是( )
A.1 B.2 C.3 D.42.下列说法不正确的是( )A.长方体与正方体都有六个面 B.圆锥的底面是圆 C.棱柱的上下底面是完全相同的图形 D.五棱柱有五个面,五条棱3.如图,建筑工人砌墙时,经常用细绳在墙的两端之间拉一条参照线,使砌的每一层砖在一条直线上,这样做蕴含的数学原理是( ) A.过一点有无数条直线 B.两点确定一条直线 C.两点之间线段最短 D.线段是直线的一部分4.下列各直线的表示法中,正确的是( )A.直线ab B.直线Ab C.直线A D.直线AB5.将如图所示放置的一个直角三角形ABC,(∠C=90°),绕斜边AB旋转一周,所得到的几何体的正视图是下面四个图中的( )
A.过一点有无数条直线 B.两点确定一条直线 C.两点之间线段最短 D.线段是直线的一部分4.下列各直线的表示法中,正确的是( )A.直线ab B.直线Ab C.直线A D.直线AB5.将如图所示放置的一个直角三角形ABC,(∠C=90°),绕斜边AB旋转一周,所得到的几何体的正视图是下面四个图中的( )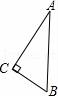 A.
A. B.
B. C.
C. D.
D. 6.如图,下面的几何体,可以由下列选项中的哪个图形绕虚线旋转一周后得到( )
6.如图,下面的几何体,可以由下列选项中的哪个图形绕虚线旋转一周后得到( )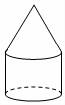 A..
A..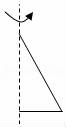 B.
B.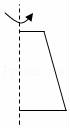 C..
C..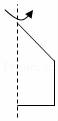 D..
D.. 7.在下列立体图形中,只要两个面就能围成的是( )A.
7.在下列立体图形中,只要两个面就能围成的是( )A.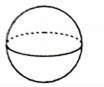 B.
B. C.
C.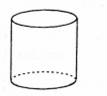 D.
D.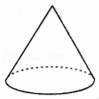 8.如图,将长方形ABCD平均分成三个小长方形,再将三个小长方形分别平均分成2份、3份和4份,阴影部分面积是长方形ABCD面积的( )
8.如图,将长方形ABCD平均分成三个小长方形,再将三个小长方形分别平均分成2份、3份和4份,阴影部分面积是长方形ABCD面积的( )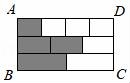 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.如图,桌面上的模型由20个棱长为a的小正方体组成,现将该模型露在外面的部分涂上涂料,则涂上涂料部分的总面积为( )
9.如图,桌面上的模型由20个棱长为a的小正方体组成,现将该模型露在外面的部分涂上涂料,则涂上涂料部分的总面积为( )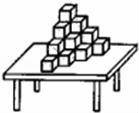 A.20a2 B.30a2 C.40a2 D.50a210.如图所示,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
A.20a2 B.30a2 C.40a2 D.50a210.如图所示,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )![]() A.点A B.点B C.AB之间 D.BC之间二.填空题11.下列图形中,是柱体的有 .(填序号)
A.点A B.点B C.AB之间 D.BC之间二.填空题11.下列图形中,是柱体的有 .(填序号) 12.如图所示的立体图形由9个棱长为1的正方体木块搭成,这个立体图形的表面积为 .
12.如图所示的立体图形由9个棱长为1的正方体木块搭成,这个立体图形的表面积为 .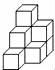 13.一个多边形有8条边,从其中的一个顶点出发,连接这个点和其他顶点,可以得到 个三角形.14.已知平面内有A、B、C、D四点,过其中的两点画一条直线,一共可以画 直线.15.如图,C是线段AB上任意一点,M,N分别是AC,BC的中点,如果AB=12cm,那么MN的长为 cm.
13.一个多边形有8条边,从其中的一个顶点出发,连接这个点和其他顶点,可以得到 个三角形.14.已知平面内有A、B、C、D四点,过其中的两点画一条直线,一共可以画 直线.15.如图,C是线段AB上任意一点,M,N分别是AC,BC的中点,如果AB=12cm,那么MN的长为 cm.![]() 16.一个五棱柱有 个顶点, 个面, 条棱.17.直角三角形绕着它的一条直角边所在直线旋转360°形成的几何体是 .18.建筑工人在砌墙时,经常在两个墙角的位置分别立一根木桩,在两根木桩之间拉一根线,沿着这条线就可以砌出直的墙.则其中的道理是: .
16.一个五棱柱有 个顶点, 个面, 条棱.17.直角三角形绕着它的一条直角边所在直线旋转360°形成的几何体是 .18.建筑工人在砌墙时,经常在两个墙角的位置分别立一根木桩,在两根木桩之间拉一根线,沿着这条线就可以砌出直的墙.则其中的道理是: .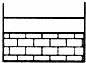 19.一个棱柱有12个面,它有 个顶点, 条棱.20.飞机表演的“飞机拉线”用数学知识解释为: .三.解答题21.某学校运动场正在建设中,运动场两端是半圆形,中间是长方形,长方形的长是100米,宽是60米.(π取3)(1)求这个运动场的周长是多少米?(2)已知整个运动场由草坪和塑胶跑道组成,塑胶跑道和草坪的面积比为2:3,每平米塑胶的价格为100元,比每平米草坪的价格高
19.一个棱柱有12个面,它有 个顶点, 条棱.20.飞机表演的“飞机拉线”用数学知识解释为: .三.解答题21.某学校运动场正在建设中,运动场两端是半圆形,中间是长方形,长方形的长是100米,宽是60米.(π取3)(1)求这个运动场的周长是多少米?(2)已知整个运动场由草坪和塑胶跑道组成,塑胶跑道和草坪的面积比为2:3,每平米塑胶的价格为100元,比每平米草坪的价格高![]() ,则购买铺满该运动场所需要的塑胶和草坪的总费用是多少元?
,则购买铺满该运动场所需要的塑胶和草坪的总费用是多少元? 22.如图所示球体上画出了三个圆,在图中的六个“□”里分别填入1,2,3,4,5,6,使得每个圆周上四个数相加的和都相等.(1)这个相等的和等于 ;(2)在图中将所有的“□”填完整.
22.如图所示球体上画出了三个圆,在图中的六个“□”里分别填入1,2,3,4,5,6,使得每个圆周上四个数相加的和都相等.(1)这个相等的和等于 ;(2)在图中将所有的“□”填完整.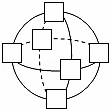 23.学校每天给班级提供一桶体积相同的饮用水,每个同学的平均饮水量和饮水人数关系如表:每个同学的平均饮水量/升
23.学校每天给班级提供一桶体积相同的饮用水,每个同学的平均饮水量和饮水人数关系如表:每个同学的平均饮水量/升![]()
![]()
![]() 饮水人数/人 2530 (1)一桶装纯净水桶可看做圆柱,高度:49cm,直径:27cm,同学们喝了一些,无水部分高29cm,喝了多少水?(2)假如每个班级学生每天将学校提供饮用水全部喝完,通过计算将表格补充完整.(要有计算过程)(3)若每桶饮用水为15元,超过18桶打八折.某班按每人每天平均饮水
饮水人数/人 2530 (1)一桶装纯净水桶可看做圆柱,高度:49cm,直径:27cm,同学们喝了一些,无水部分高29cm,喝了多少水?(2)假如每个班级学生每天将学校提供饮用水全部喝完,通过计算将表格补充完整.(要有计算过程)(3)若每桶饮用水为15元,超过18桶打八折.某班按每人每天平均饮水![]() 升计算,结果到月底共付水费240元(每月在校日按20天计算),请计算这个班级共有多少名学生?
升计算,结果到月底共付水费240元(每月在校日按20天计算),请计算这个班级共有多少名学生? 24.补画长方体.
24.补画长方体. 25.如图所示,已知直角三角形纸板ABC,直角边AB=4cm,BC=8cm.(1)将直角三角形纸板绕三角形的边所在的直线旋转一周,能得到 种大小不同的几何体?(2)分别计算绕三角形直角边所在的直线旋转一周,得到的几何体的体积?(圆锥的体积=
25.如图所示,已知直角三角形纸板ABC,直角边AB=4cm,BC=8cm.(1)将直角三角形纸板绕三角形的边所在的直线旋转一周,能得到 种大小不同的几何体?(2)分别计算绕三角形直角边所在的直线旋转一周,得到的几何体的体积?(圆锥的体积=![]() πr2h,其中π取3)
πr2h,其中π取3)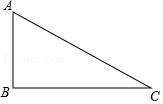 26.阅读下列材料并填空:(1)探究:平面上有n个点(n≥2)且任意3个点不在同一条直线上,经过每两点画一条直线,一共能画多少条直线?我们知道,两点确定一条直线.平面上有2个点时,可以画
26.阅读下列材料并填空:(1)探究:平面上有n个点(n≥2)且任意3个点不在同一条直线上,经过每两点画一条直线,一共能画多少条直线?我们知道,两点确定一条直线.平面上有2个点时,可以画![]() =1条直线,平面内有3个点时,一共可以画
=1条直线,平面内有3个点时,一共可以画![]() =3条直线,平面上有4个点时,一共可以画
=3条直线,平面上有4个点时,一共可以画![]() =6条直线,平面内有5个点时,一共可以画 条直线,…平面内有n个点时,一共可以画 条直线.(2)运用:某足球比赛中有22个球队进行单循环比赛(每两队之间必须比赛一场),一共要进行多少场比赛?27.六盒磁带按“规则方式”打包,所谓“规则方式”是指每相邻两盒必须以完全一样的面对接,最后得到的包装形状是一个长方形.已知磁带盒的大小为abc=11×7×2(单位cm).(1)请画出示意图,给出一种打包方式,使其表面积最小;(2)若不给出a、b、c的具体尺寸,只假定a≥b≥c,3问能否按照已知的方式打包,使其表面积最小?并说明理由.
=6条直线,平面内有5个点时,一共可以画 条直线,…平面内有n个点时,一共可以画 条直线.(2)运用:某足球比赛中有22个球队进行单循环比赛(每两队之间必须比赛一场),一共要进行多少场比赛?27.六盒磁带按“规则方式”打包,所谓“规则方式”是指每相邻两盒必须以完全一样的面对接,最后得到的包装形状是一个长方形.已知磁带盒的大小为abc=11×7×2(单位cm).(1)请画出示意图,给出一种打包方式,使其表面积最小;(2)若不给出a、b、c的具体尺寸,只假定a≥b≥c,3问能否按照已知的方式打包,使其表面积最小?并说明理由.
参考答案与试题解析一.选择题1.解:∵BF⊥FG,BF⊥EF,BF∩GF=F,∴BF⊥平面EFGH,∵BF在平面BDHF内,∴平面BDHF⊥平面EFGH;同理平面BDHF⊥平面ABCD.故选:B.2.解:A、长方体与正方体都有六个面,说法正确;B、圆锥的底面是圆,说法正确;C、棱柱的上下底面是完全相同的图形,说法正确;D、五棱柱有七个面,15条棱,说法错误.故选:D.3.解:建筑工人砌墙时,经常用细绳在墙的两端之间拉一条参照线,使砌的每一层砖在一条直线上,这种做法用几何知识解释应是:两点确定一条直线.故选:B.4.解:根据直线的表示方法可得直线AB正确.故选:D.5.解:绕斜边AB旋转一周,所得到的几何体是两个圆锥的组合体,它的正视图是两个等腰三角形,三角形之间有一条虚线段.如图: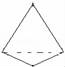 故选:C.6.解:由“面动成体”可得,选项C中的图形旋转一周可形成如图所示的几何体,故选:C.7.解:A、球是由一个曲面组成,故本选项错误;B、长方体是有六个面围成,故本选项错误;C、圆柱体是两个底面和一个侧面组成,故本选项错误;D、圆锥是一个底面和一个侧面组成,故本选项正确.故选:D.8.解:如图,阴影部分①的面积占长方形ABCD面积的
故选:C.6.解:由“面动成体”可得,选项C中的图形旋转一周可形成如图所示的几何体,故选:C.7.解:A、球是由一个曲面组成,故本选项错误;B、长方体是有六个面围成,故本选项错误;C、圆柱体是两个底面和一个侧面组成,故本选项错误;D、圆锥是一个底面和一个侧面组成,故本选项正确.故选:D.8.解:如图,阴影部分①的面积占长方形ABCD面积的![]() ,阴影部分②的面积占长方形ABCD面积的
,阴影部分②的面积占长方形ABCD面积的![]() ,阴影部分③面积占长方形ABCD面积的
,阴影部分③面积占长方形ABCD面积的![]() ,所以所有阴影部分面积是长方形ABCD面积的
,所以所有阴影部分面积是长方形ABCD面积的![]() +
+![]() +
+![]() =
=![]() ,故选:D.
,故选:D.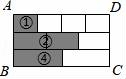 9.解:从正面、上面,后面,左面,右面看都有10个正方形,则共有50个正方形,因为每个正方形的面积为a2,则涂上涂料部分的总面积为50a2.故选:D.10.解:①以点A为停靠点,则所有人的路程的和=15×300+10×900=13500(米),②以点B为停靠点,则所有人的路程的和=30×300+10×600=15000(米),③以点C为停靠点,则所有人的路程的和=30×900+15×600=36000(米),④当在AB之间停靠时,设停靠点到A的距离是m,则(0<m<300),则所有人的路程的和是:30m+15(300﹣m)+10(900﹣m)=13500+5m>13500,⑤当在BC之间停靠时,设停靠点到B的距离为n,则(0<n<600),则总路程为30(300+n)+15n+10(600﹣n)=15000+35n>13500.∴该停靠点的位置应设在点A;故选:A.二.填空题11.解:①是圆锥,②是正方体,属于棱柱,③是圆柱,④是棱锥,⑤是球,⑥是三棱柱.所以是柱体的有②③⑥.12.解:从上面和下面看到的面积为2×5×(1×1),从正面和后面看面积为2×5×(1×1),从两个侧后面看面积为2×6×(1×1),故这个几何体的表面积为32.故答案为32.13.解:如图所示:8﹣2=6,故答案为:6.
9.解:从正面、上面,后面,左面,右面看都有10个正方形,则共有50个正方形,因为每个正方形的面积为a2,则涂上涂料部分的总面积为50a2.故选:D.10.解:①以点A为停靠点,则所有人的路程的和=15×300+10×900=13500(米),②以点B为停靠点,则所有人的路程的和=30×300+10×600=15000(米),③以点C为停靠点,则所有人的路程的和=30×900+15×600=36000(米),④当在AB之间停靠时,设停靠点到A的距离是m,则(0<m<300),则所有人的路程的和是:30m+15(300﹣m)+10(900﹣m)=13500+5m>13500,⑤当在BC之间停靠时,设停靠点到B的距离为n,则(0<n<600),则总路程为30(300+n)+15n+10(600﹣n)=15000+35n>13500.∴该停靠点的位置应设在点A;故选:A.二.填空题11.解:①是圆锥,②是正方体,属于棱柱,③是圆柱,④是棱锥,⑤是球,⑥是三棱柱.所以是柱体的有②③⑥.12.解:从上面和下面看到的面积为2×5×(1×1),从正面和后面看面积为2×5×(1×1),从两个侧后面看面积为2×6×(1×1),故这个几何体的表面积为32.故答案为32.13.解:如图所示:8﹣2=6,故答案为:6. 14.解:分三种情况:①四点在同一直线上时,只可画1条;②当三点在同一直线上,另一点不在这条直线上,可画4条;③当没有三点共线时,可画6条;故答案为:1条或4条或6条.15.解:∵点M是AC中点∴MC=
14.解:分三种情况:①四点在同一直线上时,只可画1条;②当三点在同一直线上,另一点不在这条直线上,可画4条;③当没有三点共线时,可画6条;故答案为:1条或4条或6条.15.解:∵点M是AC中点∴MC=![]() AC∵点N是BC中点∴CN=
AC∵点N是BC中点∴CN=![]() BCMN=MC+CN=
BCMN=MC+CN=![]() (AC+BC)=
(AC+BC)=![]() AB=6.所以本题应填6.16.解:故五棱柱有7个面,15条棱,10个顶点.故答案为10,7,15.17.解:直角三角形绕它的直角边旋转一周可形成圆锥.故答案为:圆锥.18.解:建筑工人在砌墙时,经常在两个墙角的位置分别立一根木桩,在两根木桩之间拉一根线,沿着这条线就可以砌出直的墙.则其中的道理是:两点确定一条直线.故答案为:两点确定一条直线.19.解:∵棱柱有12个面,∴它是十棱柱.∴十棱柱有20个顶点,30条棱.故答案为:20;30.20.解:飞机表演的“飞机拉线”用数学知识解释为:点动成线.故答案为点动成线.三.解答题21.解:(1)这个运动场的周长=
AB=6.所以本题应填6.16.解:故五棱柱有7个面,15条棱,10个顶点.故答案为10,7,15.17.解:直角三角形绕它的直角边旋转一周可形成圆锥.故答案为:圆锥.18.解:建筑工人在砌墙时,经常在两个墙角的位置分别立一根木桩,在两根木桩之间拉一根线,沿着这条线就可以砌出直的墙.则其中的道理是:两点确定一条直线.故答案为:两点确定一条直线.19.解:∵棱柱有12个面,∴它是十棱柱.∴十棱柱有20个顶点,30条棱.故答案为:20;30.20.解:飞机表演的“飞机拉线”用数学知识解释为:点动成线.故答案为点动成线.三.解答题21.解:(1)这个运动场的周长=![]() (米);(2)购买铺满该运动场所需要的塑胶和草坪的总费用:
(米);(2)购买铺满该运动场所需要的塑胶和草坪的总费用:![]() ×(π×302+100×60)=765600(元)答:购买铺满该运动场所需要的塑胶和草坪的总费用是765600元.22.解:(1)(1+2+3+4+5+6)×2÷3=21×2÷3=14;(2)如图所示:
×(π×302+100×60)=765600(元)答:购买铺满该运动场所需要的塑胶和草坪的总费用是765600元.22.解:(1)(1+2+3+4+5+6)×2÷3=21×2÷3=14;(2)如图所示: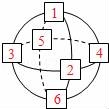 故答案为:14.23.解:(1)π×(
故答案为:14.23.解:(1)π×(![]() )2×29=
)2×29=![]() (cm3),答:喝了
(cm3),答:喝了![]() cm3的水;(2)一桶水的体积为:
cm3的水;(2)一桶水的体积为:![]() ×25=20(升),20÷
×25=20(升),20÷![]() =24(人),20÷30=
=24(人),20÷30=![]() (升/人),20÷
(升/人),20÷![]() =40(人),故答案为:24,
=40(人),故答案为:24,![]() ,40;(3)240÷(15×80%)=20(桶),20÷
,40;(3)240÷(15×80%)=20(桶),20÷![]() =50(人),答:这个班级的学生人数为50人.24.解:如图所示:
=50(人),答:这个班级的学生人数为50人.24.解:如图所示: .25.解:(1)将直角三角形纸板ABC绕三角形的三条边所在的直线旋转一周,能得到3种大小不同的几何体.故答案为:3.(2)以AB为轴:
.25.解:(1)将直角三角形纸板ABC绕三角形的三条边所在的直线旋转一周,能得到3种大小不同的几何体.故答案为:3.(2)以AB为轴:![]() ×3×82×4=
×3×82×4=![]() ×3×64×4=256(立方厘米);以BC为轴:
×3×64×4=256(立方厘米);以BC为轴:![]() ×3×42×8=
×3×42×8=![]() ×3×16×8=128(立方厘米).答:以AB为轴得到的圆锥的体积是256立方厘米,以BC为轴得到的圆锥的体积是128立方厘米.26.解:(1)平面内有5个点时,一共可以画
×3×16×8=128(立方厘米).答:以AB为轴得到的圆锥的体积是256立方厘米,以BC为轴得到的圆锥的体积是128立方厘米.26.解:(1)平面内有5个点时,一共可以画![]() 条直线,平面内有n个点时,一共可以画
条直线,平面内有n个点时,一共可以画![]() 条直线;(2)某足球比赛中有22个球队进行单循环比赛(每两队之间必须比赛一场),一共要进行
条直线;(2)某足球比赛中有22个球队进行单循环比赛(每两队之间必须比赛一场),一共要进行![]() 场比赛,故答案为:10;
场比赛,故答案为:10;![]() .27.解:(1)设:三个面的面积记为A=bc,B=ac,C=ab,①在1×6的方式下,打包方式如图乙,这时,表面积S乙=2C+12B+12A=2×11×7+12×11×2+12×7×2=586(cm2);②在2×3的方式下,打包方式如图丙,这时,表面积S丙=4C+6B+12A=4×11×7+6×11×2+12×7×2=608(cm2);因为S乙<S丙,所以最小表面积的打包方式是1×6.(2)若a≥b≥c,则单叠(即1*6方式)打包的最小表面积S=2ab+12ac+12bc;双叠(即2*3方式)打包最小表面积S'=4ab+6ac+12bc.所以S﹣S'=2a(3c﹣b).所以:当a≥b,且c≤b<3c时,最小表面积为双叠当a≥b>3c时,最小表面积为单叠当a≥b=3c时,两种方式一样大
.27.解:(1)设:三个面的面积记为A=bc,B=ac,C=ab,①在1×6的方式下,打包方式如图乙,这时,表面积S乙=2C+12B+12A=2×11×7+12×11×2+12×7×2=586(cm2);②在2×3的方式下,打包方式如图丙,这时,表面积S丙=4C+6B+12A=4×11×7+6×11×2+12×7×2=608(cm2);因为S乙<S丙,所以最小表面积的打包方式是1×6.(2)若a≥b≥c,则单叠(即1*6方式)打包的最小表面积S=2ab+12ac+12bc;双叠(即2*3方式)打包最小表面积S'=4ab+6ac+12bc.所以S﹣S'=2a(3c﹣b).所以:当a≥b,且c≤b<3c时,最小表面积为双叠当a≥b>3c时,最小表面积为单叠当a≥b=3c时,两种方式一样大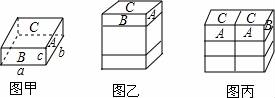
相关试卷
这是一份初中数学冀教版七年级上册5.1一元一次方程精品单元测试同步测试题,共10页。试卷主要包含了下列式子是方程的是,已知关于x的方程a+x=5﹣,下列方程变形中,正确的是,下列方程是一元一次方程的是等内容,欢迎下载使用。
这是一份冀教版七年级上册4.1 整式精品单元测试当堂检测题,共9页。试卷主要包含了下列说法中正确的是,单项式﹣的系数、次数分别是,下列各组整式中是同类项的是,下列判断正确的是,下列运算正确的是,化简﹣[﹣,下列式子中,整式有等内容,欢迎下载使用。
这是一份冀教新版七年级上册数学《第2章几何图形的初步认识》单元测试卷(有答案),共11页。试卷主要包含了圣诞帽类似于几何体,现实生活中,总有人乱穿马路,计算等内容,欢迎下载使用。










