【同步教案】湘教版（2019）高中数学 必修第二册 2.1.1 两角和与差的余弦公式 教学设计

这是一份【同步教案】湘教版（2019）高中数学 必修第二册 2.1.1 两角和与差的余弦公式 教学设计，共4页。教案主要包含了课程标准，教学目标，教学重点，教学难点，教学过程，教学反思，板书设计等内容，欢迎下载使用。
《2.1.1 两角和与差的余弦公式》教学设计一、课程标准引导学生通探索导出公式，并了解它们的内在联系，运用它们进行简单的三角恒等变形、求值.二、教学目标1．理解用向量的数量积推导两角差的余弦公式的过程，体验和感受数学发现和创造的过程，体会向量和三角函数间的联系．2．由两角差的余弦公式推出两角和的余弦公式，理解化归思想在三角变换中的作用．3．掌握用两角和与差的余弦公式进行简单的三角函数式的化简、求值及恒等式的证明．三、教学重点：两角和与差的余弦公式的推导与应用．四、教学难点：两角和与差的余弦公式的证明.五、教学过程（一）创设情境，引入新课我们会求一些特殊角的三角函数值，比如、、角的三角函数值。对于一些非特殊角的三角函数值怎么算呢，比如cos15°＝cos（45°－ 30°）=cos45°－cos30°，正确吗?那么如何用α、β的正余弦表示cos(α-β) 呢？（二）自主学习，熟悉概念1.要求：学生阅读P67-692.思考：（1）如何利用向量推导两角差的余弦公式？（2）如何利用两角差的余弦公式推导两角和的余弦公式？（三）检验自学，强化概念1. 两角差的余弦公式：如图，在直角坐标系中，取角α、β，在这两个角的终边上分别取两个单位向量,,则就是与的夹角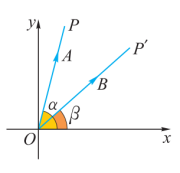，根据前面所学的向量知识可知，与的数量积为由平面向量基本定理知,                当时，所以     （简记为）2.两角和的余弦公式：在两角差的余弦公式中，用代替，就可以得到　　　　　　　（简记为）注意：①熟悉公式的结构和特点； ②此公式对任意α、β都适用3.例题讲解例1．求75º和15º的余弦值.设计意图：熟悉公式的正用，复习特殊角三角函数值.例2. 求下列各式的值.(1)；(2).设计意图：熟悉公式的逆用，复习诱导公式和特殊角三角函数值.例3.已知.且角分别是第二、四象限的角，求的值. 设计意图：熟悉两角和与差的余弦公式，复习巩固同角三角函数基本关系式和三角函数在各象限的符号.(三)课堂练习及检测P69 1,2,3(四)归纳小结1.两角和与差的余弦公式： 2.公式的正用、逆用等技巧：（五）作业1.习题2.1 2,3,2.预习2.1.2两角和与差的余弦公式：六、教学反思（酌情写一些） 七、板书设计  两角和与差的余弦公式及推导希沃课件投影区域（例1）（例2）（例3）