2022-2023学年湖北省武汉市黄陂区七年级数学第二学期期末教学质量检测模拟试题含答案

这是一份2022-2023学年湖北省武汉市黄陂区七年级数学第二学期期末教学质量检测模拟试题含答案，共6页。试卷主要包含了考生必须保证答题卡的整洁等内容，欢迎下载使用。
2022-2023学年湖北省武汉市黄陂区七年级数学第二学期期末教学质量检测模拟试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 考生请注意：1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。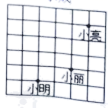 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．下列式子中，可以取和的是（   ）A． B． C． D．2．某电子产品经过连续两次降价，售价由元降到了元．设平均每月降价的百分率为，根据题意列出的方程是（    ）A． B．C． D．3．课间操时，小明、小丽、小亮的位置如图所示，小明对小亮说：如果我的位置用表示，小丽的位置用表示，那么你的位置可以表示成（   ）A． B． C． D．4．要使分式有意义，x应满足的条件是（    ）A． B． C． D．5．如图，四边形为平行四边形，延长到点，使，连接，，.添加一个条件，不能使四边形成为矩形的是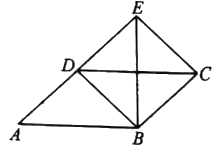（    ）A． B． C． D．6．如图，在中，，以顶点为圆心，适当长为半径画弧，分别交，于点，，再分别以点，为圆心，大于的长为半径画弧，两弧交于点，作射线交边于点，若，，则的面积是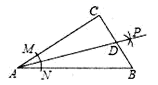（）A．15 B．30 C．45 D．607．某天小明骑自行车上学，途中因自行车发生故障，修车耽误一段时间后继续骑行，按时赶到了学校．如图描述了他上学情景，下列说法中错误的是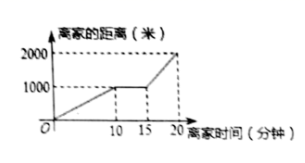（　　）A．用了5分钟来修车 B．自行车发生故障时离家距离为1000米C．学校离家的距离为2000米 D．到达学校时骑行时间为20分钟8．如图，等腰三角形的底边长为，面积是， 腰的垂直平分线分别交边于点．若点为边的中点，点为线段EF上一动点，则周长的最小值为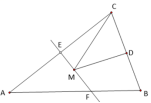（  ）A． B． C． D．9．如图， OABC的顶点O，A，C的坐标分别是（0，0），（2，0），（，1），则点B的坐标是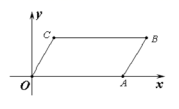（    ）A．（1，2） B．（，2） C．（，1） D．（3，1）10．甲、乙两名运动员10次比赛成绩如表，S12，S22分别表示他们测试成绩的方差，则有（     ） 8分9分10分甲（频数）424乙（频数）343A．S12>S22 B．S12=S22 C．S12<S22 D．无法确定11．函数y=5x﹣3的图象不经过（　　）A．第一象限 B．第二象限 C．第三象限 D．第四象限12．下列事件为必然事件的是（   ）A．某运动员投篮时连续3次全中 B．抛掷一块石块，石块终将下落C．今天购买一张彩票，中大奖 D．明天我市主城区最高气温为38℃二、填空题（每题4分，满分20分，将答案填在答题纸上）13．若一组数据的平均数，方差，则数据，，的方差是_________.14．若从一个多边形的一个顶点出发可引5条对角线，则它是______边形.15．已知方程的解满足x﹣y≥5，则k的取值范围为_____．16．平行四边形的一个内角平分线将对边分成3和5两个部分，则该平行四边形的周长是_____．17．如果关于的不等式组的整数解仅有,,那么适合这个不等式组的整数,组成的有序数对共有_______个；如果关于的不等式组(其中,为正整数)的整数解仅有,那么适合这个不等式组的整数,组成的有序数对共有______个.(请用含、的代数式表示)三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18．（5分）计算：（1）（2）已知a＝+2，b＝﹣2，求a2﹣b2的值．   19．（5分）如图，在矩形ABCD中，E是对角线BD上一点（不与点B、D重合），过点E作EF∥AB，且EF=AB，连接AE、BF、CF。（1）若DE=DC，求证：四边形CDEF是菱形；（2）若AB=，BC=3，当四边形ABFE周长最小时，四边形CDEF的周长为__________。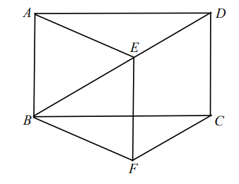   20．（8分）解不等式组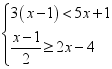，并写出它的所有非负整数解．   21．（10分）近年来雾霾天气给人们的生活带来很大影响，空气质量问题倍受人们关注．某商场计划购进一批、两种空气净化装置，每台种设备价格比每台种设备价格多0.7万元，花3万元购买种设备和花7.2万元购买种设备的数量相同．（1）求种、种设备每台各多少万元？（2）根据销售情况，需购进、两种设备共20台，总费用不高于15万元，求种设备至少要购买多少台？（3）若每台种设备售价0.6万元，每台种设备售价1.4万元，在（2）的情况下商场应如何进货才能使这批空气净化装置售完后获利最多？   22．（10分）如图，已知□ABCD.（1）作图：延长BC，并在BC的延长线上截取线段CE，使得CE=BC．（用尺规作图法，保留作图痕迹，不要求写作法）；（2）在（1）的条件下，连结AE，交CD于点F，求证:△AFD ≌ △EFC.   23．（12分）如图，在中，AB=2AD，DE平分∠ADC，交AB于点E，交CB的延长线于点F，EG∥AD交DC于点G.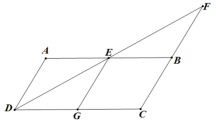⑴求证：四边形AEGD为菱形；⑵若，AD=2，求DF的长.   参考答案 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1、C2、B3、C4、D5、C6、B7、D8、C9、C10、A11、B12、B 二、填空题（每题4分，满分20分，将答案填在答题纸上）13、14、八.    .15、k≥116、22或1．17、6    pq     三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18、（1）原式＝5；（2）原式＝819、（1）见解析；（2）20、非负整数解是：0，1、1．21、（1）种设备每台0.5万元，种设备每台l.2万元；（2）种设备至少购买13台；（3）当购买种设备13台，种设备７台时，获利最多．22、（1）作图解析；（2）证明见解析.23、（1）证明见解析；（2）4．