


2022-2023学年浙江省衢州市七年级数学第二学期期末综合测试试题含答案
展开
这是一份2022-2023学年浙江省衢州市七年级数学第二学期期末综合测试试题含答案,共7页。试卷主要包含了下列调查适合抽样调查的是,下列图案中,中心对称图形的是等内容,欢迎下载使用。
2022-2023学年浙江省衢州市七年级数学第二学期期末综合测试试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。 一、选择题(每小题3分,共30分)1.已知![]() 为矩形
为矩形![]() 的对角线,则图中
的对角线,则图中![]() 与
与![]() 一定不相等的是( )A.
一定不相等的是( )A.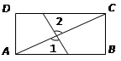 B.
B.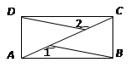 C.
C.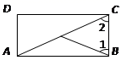 D.
D.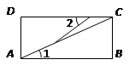 2.下列式子中一定是二次根式的是( )A.
2.下列式子中一定是二次根式的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.一个直角三角形的两边长分别为2和
3.一个直角三角形的两边长分别为2和![]() ,则第三边的长为( )A.1 B.2 C.
,则第三边的长为( )A.1 B.2 C.![]() D.34.如图,O是正六边形ABCDEF的中心,下列三角形中可由△OBC平移得到的是( )
D.34.如图,O是正六边形ABCDEF的中心,下列三角形中可由△OBC平移得到的是( )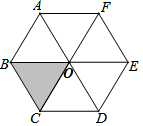 A.△OCD B.△OAB C.△OAF D.△OEF5.如图是我国一位古代数学家在注解《周髀算经》时给出的,曾被选为2002年在北京召开的国际数学家大会的会徽,它通过对图形的切割、拼接,巧妙地证明了勾股定理,这位伟大的数学家是( )
A.△OCD B.△OAB C.△OAF D.△OEF5.如图是我国一位古代数学家在注解《周髀算经》时给出的,曾被选为2002年在北京召开的国际数学家大会的会徽,它通过对图形的切割、拼接,巧妙地证明了勾股定理,这位伟大的数学家是( )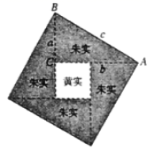 A.杨辉 B.刘徽 C.祖冲之 D.赵爽6.下列调查适合抽样调查的是( )A.审核书稿中的错别字B.对某校八一班同学的身高情况进行调查C.对某校的卫生死角进行调查D.对全县中学生目前的睡眠情况进行调查7.若直线y=x+1与y=-2x+a的交点在第一象限,则a的取值可以是
A.杨辉 B.刘徽 C.祖冲之 D.赵爽6.下列调查适合抽样调查的是( )A.审核书稿中的错别字B.对某校八一班同学的身高情况进行调查C.对某校的卫生死角进行调查D.对全县中学生目前的睡眠情况进行调查7.若直线y=x+1与y=-2x+a的交点在第一象限,则a的取值可以是 ![]() A.-1 B.0 C.1 D.28.如图,▱ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=
A.-1 B.0 C.1 D.28.如图,▱ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②S▱ABCD=AB•AC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②S▱ABCD=AB•AC;③OB=AB;④OE=![]() BC,成立的个数有()
BC,成立的个数有() A.1个B.2个C.3个D.4个9.下列图案中,中心对称图形的是( )A.
A.1个B.2个C.3个D.4个9.下列图案中,中心对称图形的是( )A. B.
B. C.
C. D.
D. 10.某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资S(吨)与时间t(小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
10.某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资S(吨)与时间t(小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )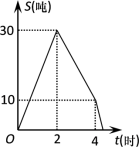 A.4小时 B.4.4小时 C.4.8小时 D.5小时二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,EF⊥AD,将平行四边形ABCD沿着EF对折.设∠1的度数为n°,则∠C=______.(用含有n的代数式表示)
A.4小时 B.4.4小时 C.4.8小时 D.5小时二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,EF⊥AD,将平行四边形ABCD沿着EF对折.设∠1的度数为n°,则∠C=______.(用含有n的代数式表示)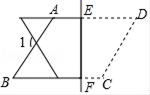 12.按一定规律排列的一列数:
12.按一定规律排列的一列数:![]() ,
,![]() ,3,
,3,![]() ,
,![]() ,
,![]() ,…那么第9个数是____________.13.实数a、b在数轴上的位置如图所示,化简
,…那么第9个数是____________.13.实数a、b在数轴上的位置如图所示,化简![]() =_____.
=_____.![]() 14.如图,
14.如图,![]() ,以点
,以点![]() 为圆心, 任意长为半径画弧, 交
为圆心, 任意长为半径画弧, 交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,再分别以点
,再分别以点![]() 、
、![]() 为圆心,大于
为圆心,大于![]() 长为半径画弧交于点
长为半径画弧交于点![]() ,过点
,过点![]() 作射线
作射线![]() ,在射线
,在射线![]() 上截取
上截取![]() ,过点
,过点![]() 作
作![]() , 垂足为点
, 垂足为点![]() , 则
, 则![]() 的长为________________.
的长为________________.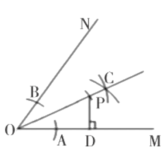 15.如图,点P是等边三角形ABC内一点,且PA=3,PB=4, PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.
15.如图,点P是等边三角形ABC内一点,且PA=3,PB=4, PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.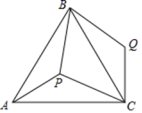 16.在学习了平行四边形的相关内容后,老师提出这样一个问题:“四边形ABCD是平行四边形,请添加一个条件,使得▱ABCD是矩形.”经过思考,小明说:“添加AC=BD.”小红说:“添加AC⊥BD.”你同意______的观点,理由是______.三、解下列各题(本大题共8小题,共72分)17.(8分)甲、乙两名运动员进行长跑训练,两人距终点的路程
16.在学习了平行四边形的相关内容后,老师提出这样一个问题:“四边形ABCD是平行四边形,请添加一个条件,使得▱ABCD是矩形.”经过思考,小明说:“添加AC=BD.”小红说:“添加AC⊥BD.”你同意______的观点,理由是______.三、解下列各题(本大题共8小题,共72分)17.(8分)甲、乙两名运动员进行长跑训练,两人距终点的路程![]() (米)与跑步时间
(米)与跑步时间![]() (分)之间的函数关系如图所示,根据图象所提供的信息解答问题:
(分)之间的函数关系如图所示,根据图象所提供的信息解答问题: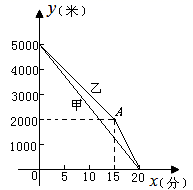 (1)他们在进行 米的长跑训练,在0<
(1)他们在进行 米的长跑训练,在0<![]() <15的时间内,速度较快的人是 (填“甲”或“乙”);(2)求乙距终点的路程
<15的时间内,速度较快的人是 (填“甲”或“乙”);(2)求乙距终点的路程![]() (米)与跑步时间
(米)与跑步时间![]() (分)之间的函数关系式;(3)当
(分)之间的函数关系式;(3)当![]() =15时,两人相距多少米?(4)在15<
=15时,两人相距多少米?(4)在15<![]() <20的时间段内,求两人速度之差. 18.(8分)如图,在△AOB中,∠ABO=90°,OB=1,AB=8,反比例函数y=
<20的时间段内,求两人速度之差. 18.(8分)如图,在△AOB中,∠ABO=90°,OB=1,AB=8,反比例函数y=![]() 在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=1.(1)求反比例函数解析式;(2)求点C的坐标.
在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=1.(1)求反比例函数解析式;(2)求点C的坐标.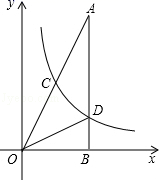 19.(8分)如图,在
19.(8分)如图,在![]() 中,
中,![]() 是
是![]() 边上的中线,
边上的中线,![]() 的垂直平分线分别交
的垂直平分线分别交![]() 于点
于点![]() ,连接
,连接![]() .(1)求证:点
.(1)求证:点![]() 在
在![]() 的垂直平分线上;(2)若
的垂直平分线上;(2)若![]() ,请直接写出
,请直接写出![]() 的度数.
的度数.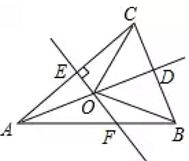 20.(8分)古埃及人用下面的方法得到直角三角形,把一根长绳打上等距离的13个结(12段),然后用桩钉钉成一个三角形,如图1,其中∠C便是直角.
20.(8分)古埃及人用下面的方法得到直角三角形,把一根长绳打上等距离的13个结(12段),然后用桩钉钉成一个三角形,如图1,其中∠C便是直角.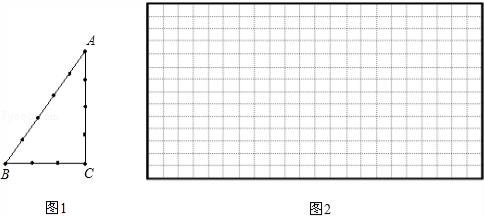 (1)请你选择古埃及人得到直角三角形这种方法的理由 (填A或B)A.勾股定理:在直角三角形边的两直角边的平方和等于斜边的平方B.勾股定理逆定理:如果三角形的三边长a、b、c有关系:a2+b2=c2,那么这个三角形是直角三角形(2)如果三个正整数a、b、c满足a2+b2=c2,那么我们就称 a、b、c是一组勾股数,请你写出一组勾股数 (3)仿照上面的方法,再结合上面你写出的勾股数,你能否只用绳子,设计一种不同于上面的方法得到一个直角三角形(在图2中,只需画出示意图.) 21.(8分)先化简,再求值:
(1)请你选择古埃及人得到直角三角形这种方法的理由 (填A或B)A.勾股定理:在直角三角形边的两直角边的平方和等于斜边的平方B.勾股定理逆定理:如果三角形的三边长a、b、c有关系:a2+b2=c2,那么这个三角形是直角三角形(2)如果三个正整数a、b、c满足a2+b2=c2,那么我们就称 a、b、c是一组勾股数,请你写出一组勾股数 (3)仿照上面的方法,再结合上面你写出的勾股数,你能否只用绳子,设计一种不同于上面的方法得到一个直角三角形(在图2中,只需画出示意图.) 21.(8分)先化简,再求值:![]() ,其中
,其中![]() 的值从不等式组
的值从不等式组![]() 的整数解中选取. 22.(10分)
的整数解中选取. 22.(10分)![]() 23.(10分)在学习了正方形后,数学小组的同学对正方形进行了探究,发现:(1)如图1,在正方形ABCD中,点E为BC边上任意一点(点E不与B、C重合),点F在线段AE上,过点F的直线MN⊥AE,分别交AB、CD于点M、N . 此时,有结论AE=MN,请进行证明; (2)如图2:当点F为AE中点时,其他条件不变,连接正方形的对角线BD, MN 与BD交于点G,连接BF,此时有结论:BF= FG,请利用图2做出证明.(3)如图3:当点E为直线BC上的动点时,如果(2)中的其他条件不变,直线MN分别交直线AB、CD于点M、N,请你直接写出线段AE与MN之间的数量关系、线段BF与FG之间的数量关系.
23.(10分)在学习了正方形后,数学小组的同学对正方形进行了探究,发现:(1)如图1,在正方形ABCD中,点E为BC边上任意一点(点E不与B、C重合),点F在线段AE上,过点F的直线MN⊥AE,分别交AB、CD于点M、N . 此时,有结论AE=MN,请进行证明; (2)如图2:当点F为AE中点时,其他条件不变,连接正方形的对角线BD, MN 与BD交于点G,连接BF,此时有结论:BF= FG,请利用图2做出证明.(3)如图3:当点E为直线BC上的动点时,如果(2)中的其他条件不变,直线MN分别交直线AB、CD于点M、N,请你直接写出线段AE与MN之间的数量关系、线段BF与FG之间的数量关系.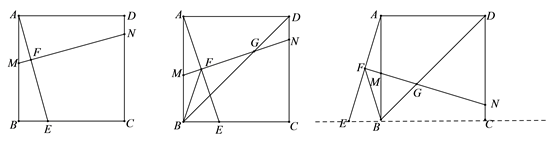 图1 图2 图3 24.(12分)解分式方程:
图1 图2 图3 24.(12分)解分式方程: ![]() 参考答案 一、选择题(每小题3分,共30分)1、D2、A3、C4、C5、D6、D7、D8、C9、A10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、180°﹣
参考答案 一、选择题(每小题3分,共30分)1、D2、A3、C4、C5、D6、D7、D8、C9、A10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、180°﹣![]() n°12、
n°12、![]() .13、-b14、5cm15、150°16、小明 对角线相等的平行四边形是矩形. 三、解下列各题(本大题共8小题,共72分)17、(1)5000;甲;(2)
.13、-b14、5cm15、150°16、小明 对角线相等的平行四边形是矩形. 三、解下列各题(本大题共8小题,共72分)17、(1)5000;甲;(2)![]() ;(3)750米;(4)150米/分.18、(1)反比例函数解析式为y=
;(3)750米;(4)150米/分.18、(1)反比例函数解析式为y=![]() ;(2)C点坐标为(2,1)19、(1)详见解析;(2)
;(2)C点坐标为(2,1)19、(1)详见解析;(2)![]() 20、(1)B(2)(6,8,10)(3)见解析21、
20、(1)B(2)(6,8,10)(3)见解析21、![]() ,-222、323、(1)证明见解析;(2)证明见解析;(3)AE与 MN的数量关系是:AE= MN ,BF与FG的数量关系是: BF= FG24、
,-222、323、(1)证明见解析;(2)证明见解析;(3)AE与 MN的数量关系是:AE= MN ,BF与FG的数量关系是: BF= FG24、![]()
相关试卷
这是一份浙江省衢州市初三数2022-2023学年数学七年级第二学期期末学业水平测试模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,一组数据,下列各式中,一定是二次根式的是等内容,欢迎下载使用。
这是一份浙江省衢州市名校2022-2023学年数学七年级第二学期期末调研模拟试题含答案,共7页。试卷主要包含了下列计算中正确的是,正方形具有而菱形不具有的性质是,下列命题是假命题的是等内容,欢迎下载使用。
这是一份浙江省衢州市教联盟体2022-2023学年数学七年级第二学期期末检测试题含答案,共7页。








