2022-2023学年浙江省宁波市奉化区七年级数学第二学期期末达标测试试题含答案

2022-2023学年浙江省宁波市奉化区七年级数学第二学期期末达标测试试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考试结束后，请将本试卷和答题卡一并交回．

2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．

3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．

4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．

5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．

一、选择题(每小题3分,共30分)

1．下列命题中，假命题的是（　　）

A．矩形的对角线相等

B．平行四边形的对角线互相平分

C．对角线互相垂直平分的四边形是菱形

D．对角线相等且互相垂直的四边形是正方形

2．已知样本数据1，2，4，3，5，下列说法不正确的是（ ）

A．平均数是3 B．中位数是4

C．极差是4 D．方差是2

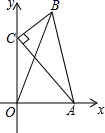
3．如图，在△ABC中，∠C=90°，AC=4，BC=2，点A、C分别在x轴、y轴上，当点A在x轴上运动时，点C随之在y轴上运动.在运动过程中，点B到原点的最大距离是(     )

A．6 B．2 C．2 D．2＋2

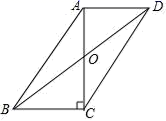
4．如图，▱ABCD的对角线AC与BD相交于点O，AC⊥BC，且AB＝10，AD＝6，则OB的长度为（　　）

A．2 B．4 C．8 D．4

5．等式成立的条件是(　　)

A． B． C．x＞2 D．

6．若a，b为等腰△ABC的两边，且满足|a﹣5|+＝0，则△ABC的周长为（　　）

A．9 B．12 C．15或12 D．9或12

7．已知，如图，正方形的面积为25，菱形的面积为20，求阴影部分的面积（）

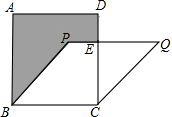
A．11 B．6.5 C．7 D．7.5

8．下列各式中，正确的是（　　）

A． B． C． D．

9．如图，不能判定△AOB和△DOC相似的条件是（   ）

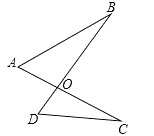
A．AO•CO=BO•DO B． C．∠A=∠D D．∠B=∠C

10．某班5位学生参加中考体育测试的成绩(单位：分)分别是：50、45、36、48、50，则这组数据的众数是（   ）

A．36 B．45 C．48 D．50

二、填空题(本大题共有6小题，每小题3分，共18分)

11．为参加学校举办的“诗意校园·致远方”朗诵艺术大赛,“屈原读书社”组织了五次选拔赛,这五次选拔赛中,小明五次成绩的平均数是90分,方差是2；小强五次成绩的平均数也是90分,方差是14.8,则小明和小强的成绩中,__________的成绩更稳定.

12．如图，矩形边，，沿折叠，使点与点重合，点的对应点为，将绕着点顺时针旋转，旋转角为．记旋转过程中的三角形为，在旋转过程中设直线与射线、射线分别交于点、，当时，则的长为_______．

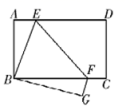
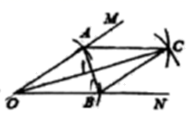
13．如图，在的两边上分别截取、，使；分别以点、为圆心，长为半径作弧，两弧交于点，连接、.若，四边形的面积为.则的长为______.

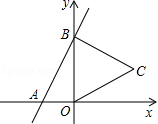
14．如图，直线y=2x+4与x，y轴分别交于A，B两点，以OB为边在y轴右侧作等边三角形OBC，将点C向左平移，使其对应点C′恰好落在直线AB上，则点C′的坐标为　   　．

15．在一个矩形中，若一个角的平分线把一条边分成长为3cm和4cm的两条线段，则该矩形周长为_________

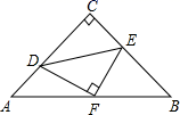
16．如图，已知△ABC中，AC=BC，∠ACB=90°，直角∠DFE的顶点F是AB中点，两边FD，FE分别交AC，BC于点D，E两点，当∠DFE在△ABC内绕顶点F旋转时（点D不与A，C重合），给出以下个结论：①CD=BE；②四边形CDFE不可能是正方形；③△DFE是等腰直角三角形；④S四边形CDFE=S△ABC．上述结论中始终正确的有______．（填序号）

三、解下列各题(本大题共8小题，共72分)

17．（8分）如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(－2，1)，B(－1，4)，C(－3，3)．

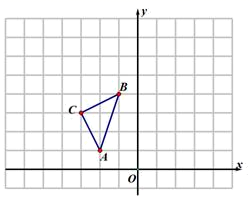
（1）画出△ABC绕点B逆时针旋转90°得到的△A1BC1.

（2）以原点O为位似中心，位似比为2:1，在y轴的左侧，画出将△ABC放大后的△A2B2C2，并写出A2点的坐标_________.

18．（8分）甲、乙两家草莓采摘园的草莓品质相同，销售价格也相同．“五一期间”，两家均推出了优惠方案，甲采摘园的优惠方案是：游客进园需购买50元的门票，采摘的草莓六折优惠；乙采摘园的优惠方案是：游客进园不需购买门票，采摘园的草莓超过一定数量后，超过部分打折优惠．优惠期间，设某游客的草莓采摘量为x（千克），在甲采摘园所需总费用为（元），在乙采摘园所需总费用为（元），图中折线OAB表示与x之间的函数关系．

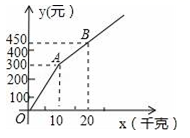
（1）甲、乙两采摘园优惠前的草莓销售价格是每千克       元；

（2）求、与x的函数表达式；

（3）在图中画出与x的函数图象，并写出选择甲采摘园所需总费用较少时，草莓采摘量x的范围．

19．（8分）在四边形中，对角线、相交于点，过点的直线分别交边、、、于点、、、

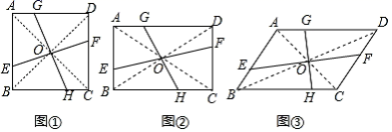
(1)如图①，若四边形是正方形，且，易知，又因为，所以（不要求证明）

(2)如图②，若四边形是矩形，且，若，，，求的长（用含、、的代数式表示）；

(3)如图③，若四边形是平行四边形，且，若，，，则　   　．

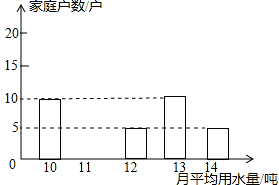
20．（8分）为了倡导“节约用水，从我做起”，南沙区政府决定对区直属机关300户家庭的用水情况作一次调查，区政府调查小组随机抽查了其中50户家庭一年的月平均用水量（单位：吨），调查中发现每户用水量均在10﹣14吨/月范围，并将调查结果制成了如图所示的条形统计图．

（1）请将条形统计图补充完整；

（2）这50户家庭月用水量的平均数是　   　，众数是　   　，中位数是　   　；

（3）根据样本数据，估计南沙区直属机关300户家庭中月平均用水量不超过12吨的约有多少户？

21．（8分）已知反比例函数为常数，且).

 (1)若在其图像的每个分支上，随的增大而增大，求的取值范围.

 (2)若其图象与一次函数y=−x+1图象的一个交点的纵坐标是3，求m的值。

22．（10分）如图，是边长为的等边三角形.

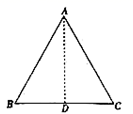
（1）求边上的高与之间的函数关系式。是的一次函数吗？如果是一次函数，请指出相应的与的值.

（2）当时，求的值.

（3）求的面积与之间的函数关系式.是的一次函数吗？

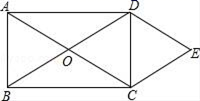
23．（10分）如图所示，O为矩形ABCD对角线的交点，DE∥AC，CE∥BD．

（1）试判断四边形OCED的形状，并说明理由；

（2）若AB＝3，BC＝4，求四边形OCED的周长．

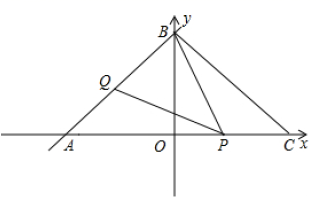
24．（12分）如图，一次函数的图象与，轴分别交于，两点，点与点关于轴对称.动点，分别在线段，上（点与点，不重合），且满足.

（1）求点，的坐标及线段的长度；

（2）当点在什么位置时，，说明理由；

（3）当为等腰三角形时，求点的坐标.

参考答案

一、选择题(每小题3分,共30分)

1、D

2、B

3、D

4、A

5、C

6、B

7、A

8、D

9、B

10、D

二、填空题(本大题共有6小题，每小题3分，共18分)

11、小明

12、

13、1

14、（﹣2，2）

15、20或22

16、①③④

三、解下列各题(本大题共8小题，共72分)

17、（1）见解析；（2）见解析，（-4，2）

18、（1）1；（2），；（3）＜x＜．

19、（1）见解析；（2）；（3）

20、 (1)补图见解析；（2）11.6，11，11；（）210户.

21、（1）m<5；（2）m=-1

22、（1），是的一次函数，，b=0；（2）x=2；（3），不是的一次函数.

23、（1）菱形（2）1

24、（1）10；（2）当点的坐标是时，；（3）点的坐标是或.