


2022-2023学年江苏省苏州昆山、太仓市七下数学期末联考模拟试题含答案
展开2022-2023学年江苏省苏州昆山、太仓市七下数学期末联考模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.下列图形中,是中心对称但不是轴对称图形的有( )

A.1个 B.2个 C.3个 D.4个
2.如图所示,在![]() 中,
中,![]() ,
,![]() 、
、![]() 是斜边
是斜边![]() 上的两点,且
上的两点,且![]() ,将
,将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 后得到
后得到![]() ,连接
,连接![]() .有下列结论:①
.有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 其中正确的有( )
其中正确的有( )
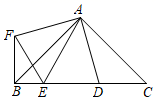
A.①②③④ B.②③ C.②③④ D.②④
3.下列语句正确的是( )
A.对角线互相垂直的四边形是菱形
B.有两对邻角互补的四边形为平行四边形
C.矩形的对角线相等
D.平行四边形是轴对称图形
4.下列二次根式①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,能与
,能与![]() 合并的是( )
合并的是( )
A.①和② B.②和③ C.①和④ D.③和④
5.设正比例函数y=mx的图象经过点A(m,4),且y的值随x的增大而增大,则m=( )
A.2 B.-2 C.4 D.-4
6.如图所示,已知四边形ABCD的对角线AC、BD相交于点O,则下列能判断它是正方形的条件是( )
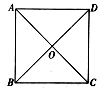
A.![]() ,
,![]() B.
B.![]()
C.![]() ,
,![]() ,
,![]() D.
D.![]() ,
,![]()
7.一个菱形的边长为![]() ,面积为
,面积为![]() ,则该菱形的两条对角线的长度之和为( )
,则该菱形的两条对角线的长度之和为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.如图,在△ABC中,AB=8,∠C=90°,∠A=30°,DE是中位线,则DE的长为( )
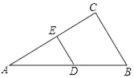
A.2 B.3 C.4 D.2![]()
9.下列选项中的图形,不属于中心对称图形的是( )
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
10.如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的角平分线AF与AB的垂直平分线DF交于点F,连接CF,BF,则∠BCF的度数为( )
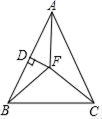
A.30° B.40° C.50° D.45°
二、填空题(本大题共有6小题,每小题3分,共18分)
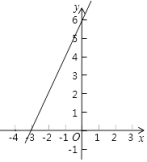
11.一次函数y=2x+6的图象如图所示,则不等式2x+6>0的解集是________,当y≤3时,x的取值范围是________.
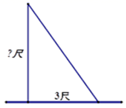
12.我国古代数学著作《九章算术》有一个问题:一根竹子高1丈,折断后竹子顶端落在离竹子底端3尺处,1丈=10尺,那么折断处离地面的高度是__________尺.
13.正比例函数![]() 图象与反比例函数
图象与反比例函数![]() 图象的一个交点的横坐标为
图象的一个交点的横坐标为![]() ,则
,则![]() ______.
______.
14.两个相似三角形的周长分别为8和6,若一个三角形的面积为36,则另一个三角形的面积为________.
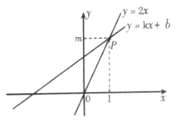
15.如图,直线y=kx+b与直线y=2x交于点P(1,m),则不等式2x<kx+b的解集为______.
16.方程![]() 的解为_________.
的解为_________.
三、解下列各题(本大题共8小题,共72分)
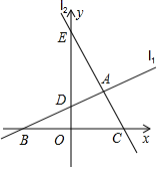
17.(8分)如图,已知函数![]() 的图象为直线
的图象为直线![]() ,函数
,函数![]() 的图象为直线
的图象为直线![]() ,直线
,直线![]() 、
、![]() 分别交
分别交![]() 轴于点
轴于点![]() 和点
和点![]() ,分别交
,分别交![]() 轴于点
轴于点![]() 和
和![]() ,
,![]() 和
和![]() 相交于点
相交于点![]()
(1)填空:![]() ;求直线
;求直线![]() 的解析式为 ;
的解析式为 ;
(2)若点![]() 是
是![]() 轴上一点,连接
轴上一点,连接![]() ,当
,当![]() 的面积是
的面积是![]() 面积的2倍时,请求出符合条件的点
面积的2倍时,请求出符合条件的点![]() 的坐标;
的坐标;
(3)若函数![]() 的图象是直线
的图象是直线![]() ,且
,且![]() 、
、![]() 、
、![]() 不能围成三角形,直接写出
不能围成三角形,直接写出![]() 的值.
的值.
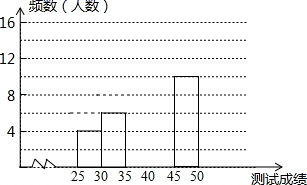
18.(8分)为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 6 |
第3组 | 35≤x<40 | 14 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
19.(8分)某水厂为了了解![]() 小区居民的用水情况,随机抽查了
小区居民的用水情况,随机抽查了![]() 小区10户家庭的月用水量,结果如下表:
小区10户家庭的月用水量,结果如下表:
月用水量( | 10 | 13 | 14 | 17 | 18 |
户数 | 2 | 2 | 3 | 2 | 1 |
如果![]() 小区有500户家庭,请你估计
小区有500户家庭,请你估计![]() 小区居民每月(按30天计算)共用水多少立方米?(答案用科学记数法表示)
小区居民每月(按30天计算)共用水多少立方米?(答案用科学记数法表示)
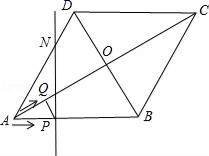
20.(8分)如图,菱形ABCD的边长为20cm,∠ABC=120°.动点P、Q同时从点A出发,其中P以4cm/s的速度,沿A→B→C的路线向点C运动;Q以2![]() cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.
cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.
(1)在点P、Q运动过程中,请判断PQ与对角线AC的位置关系,并说明理由;
(2)若点Q关于菱形ABCD的对角线交点O的对称点为M,过点P且垂直于AB的直线l交菱形ABCD的边AD(或CD)于点N.
①当t为何值时,点P、M、N在一直线上?
②当点P、M、N不在一直线上时,是否存在这样的t,使得△PMN是以PN为一直角边的直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
21.(8分)如图,在平面直角坐标系中,![]() 为坐标原点,矩形
为坐标原点,矩形![]() 的顶点
的顶点![]() ,将矩形
,将矩形![]() 的一个角沿直线
的一个角沿直线![]() 折叠,使得点
折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕与
处,折痕与![]() 轴交于点
轴交于点![]() .
.
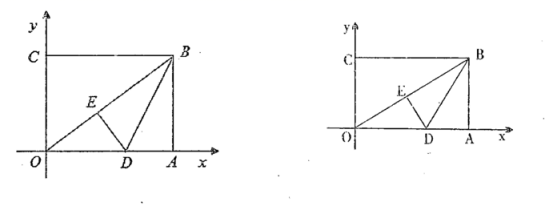
(1)求直线![]() 所对应的函数表达式;
所对应的函数表达式;
(2)若点![]() 在线段
在线段![]() 上,在线段
上,在线段![]() 上是否存在点
上是否存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形?若存在,请求出点
为顶点的四边形是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
22.(10分)某移动通信公司推出了如下两种移动电话计费方式,
| 月使用费/元 | 主叫限定时间/分钟 | 主叫超时费(元/分钟) |
方式一 | 30 | 600 | 0.20 |
方式二 | 50 | 600 | 0.25 |
说明:月使用费固定收取,主叫不超过限定时间不再收费,超过部分加收超时费.例如,方式一每月固定交费30元,当主叫计时不超过300分钟不再额外收费,超过300分钟时,超过部分每分钟加收0.20元(不足1分钟按1分钟计算)
(1)请根据题意完成如表的填空;
| 月主叫时间500分钟 | 月主叫时间800分钟 |
方式一收费/元 |
| 130 |
方式二收费/元 | 50 |
|
(2)设某月主叫时间为t(分钟),方式一、方式二两种计费方式的费用分别为y1(元),y2(元),分别写出两种计费方式中主叫时间t(分钟)与费用为y1(元),y2(元)的函数关系式;
(3)请计算说明选择哪种计费方式更省钱.
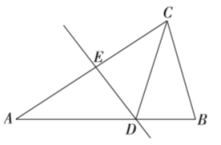
23.(10分)如图,![]() ,
,![]() 是
是![]() 上的一点,且
上的一点,且![]() ,
,![]() .
.
求证:![]() ≌
≌![]()
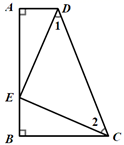
24.(12分)如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的垂直平分线.
的垂直平分线.
(1)求证:![]() 是等腰三角形.
是等腰三角形.
(2)若![]() 的周长是
的周长是![]() ,
,![]() ,求
,求![]() 的周长.(用含
的周长.(用含![]() ,
,![]() 的代数式表示)
的代数式表示)
参考答案
一、选择题(每小题3分,共30分)
1、B
2、C
3、C
4、C
5、A
6、A
7、C
8、A
9、B
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、x>﹣3 x≤﹣![]()
12、4.1
13、4
14、64或![]()
15、x<1
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ;(2)
;(2)![]() 点的坐标为
点的坐标为![]() 或
或![]() ;(3)
;(3)![]() 的值为
的值为![]() 或
或![]() 或
或![]() .
.
18、(1)16;(2)详见解析;(3)52%
19、该小区居民每月共用水约为![]() 立方米.
立方米.
20、(1)在点P、Q运动过程中,始终有PQ⊥AC;理由见解析;(1)①当t=![]() 时,点P、M、N在一直线上;② 存在这样的t,故 当t=1或
时,点P、M、N在一直线上;② 存在这样的t,故 当t=1或![]() 时,存在以PN为一直角边的直角三角形.
时,存在以PN为一直角边的直角三角形.
21、(1)y=2x-1;(2)存在点![]() ,Q(
,Q(![]() ,
,![]() ), 使以
), 使以![]() 为顶点的四边形为平行四边形.
为顶点的四边形为平行四边形.
22、(1)70;100;(2)详见解析;(3)当0≤t≤400时方式一省钱;当400<t≤1400时,方式二省钱,当t>1400时,方式一省钱,当为400分钟、1400分钟时,两种方式费用相同.
23、证明见解析.
24、(1)详见解析;(2)a+b
江苏省苏州市昆山市、太仓市2023-2024学年数学九上期末联考模拟试题含答案: 这是一份江苏省苏州市昆山市、太仓市2023-2024学年数学九上期末联考模拟试题含答案,共7页。试卷主要包含了方程x2=3x的解为,一元二次方程的根的情况是等内容,欢迎下载使用。
江苏省苏州昆山市石牌中学2022-2023学年七下数学期末检测模拟试题含答案: 这是一份江苏省苏州昆山市石牌中学2022-2023学年七下数学期末检测模拟试题含答案,共6页。试卷主要包含了函数y=x-1的图象是,下列命题,是真命题的是等内容,欢迎下载使用。
江苏省苏州市昆山市、太仓市2022-2023学年七下数学期末综合测试模拟试题含答案: 这是一份江苏省苏州市昆山市、太仓市2022-2023学年七下数学期末综合测试模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,下列多项式能分解因式的是等内容,欢迎下载使用。












