七年级数学（人教版）上册同步试卷 第四章 章末检测 几何图形初步单元测试

第四章 几何图形初步单元测试

一、选择题（本大题共14个小题，每题2分，共28分，在每个小题的四个选项中只有一项是符合题目要求的）

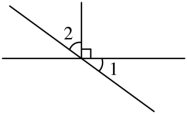
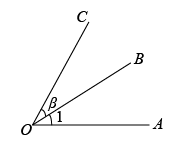
1．（2022·陕西·商南县富水镇初级中学七年级期末）如图，若，则∠2的度数是（   ）

A． B．

C． D．

2．（2020·吉林白城·七年级期末）下图是一个三棱柱纸盒的示意图，则这个纸盒的平面展开图是（    ）

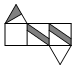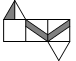A． B． C． D．

3．（2022·辽宁·沈阳市培英中学七年级期中）如果一个角的补角是这个角余角的2.5倍，那么这个角的度数是（    ）

A．30° B．60° C．90° D．120°

4．（2022·全国·七年级专题练习）如下图，下列说法正确的是（   ）

A．与表示同一个角 B．

C．图中共有两个角：， D．表示

5．（2022·广东·九年级专题练习）一个六棱柱，底面边长都是厘米，侧棱长为厘米，这个六棱柱的所有侧面的面积之和是（    ）

A． B． C． D．

6．（2020·山东济宁·七年级开学考试）把一个底面半径是5厘米，高10厘米的圆柱底面分成许多相等的扇形（如下图），切开后，再拼起来，得到一个近似的长方体．拼成后这个长方体的表面积与原来的圆柱体表面积相比，结果（    ）．

A．不变 B．变小 C．变大

7．（2022·山东·单县湖西学校七年级期中）如图，C，D是线段AB上的两点，E是AC的中点，F是BD的中点，若，则线段AB的长为（    ）

A．12 B．10 C．8 D．7

8．（2022·广西河池·七年级期末）平面内有4条直线，这4条直线两两相交，最多可以得到a个交点，最少可以得到b个交点，则的值是（    ）

A．5 B．6 C．7 D．8

9．（2022·全国·七年级期中）棱长为3英寸的正方体是由27个单位小正方体组成的，其中有21个红色小正方体，6个白色小正方体，若让大正方体的表面尽可能少地出现白色，则大正方体表面积中白色部分占整个正方体表面积的（　　）

A． B． C． D．

10．（2022·全国·七年级专题练习）每天中午12点30分是“校园之声”节目都会如约而至，此时时针与分针所夹的的角为(    )

A． B． C． D．

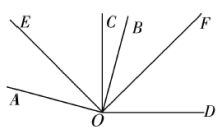
11．（2022·河南郑州·七年级期末）如图，若，且，求的度数为（    ）

A． B． C． D．

12．（2022·山东滨州·七年级期末）如图，线段的长为，点为上一动点（不与，重合），为中点，为中点，随着点的运动，线段的长度（   ）

A．随之变化 B．不改变，且为

C．不改变，且为 D．不改变，且为

13．（2022·全国·七年级单元测试）如图，长方形纸片，点、分别在边、上，连接．将对折，点落在直线上的点处，得折痕；将对折，点落在直线上的点处，得折痕．则的度数为（    ）

A． B． C． D．不能确定

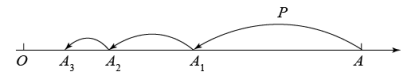
14．（2021·云南昆明·七年级期末）如图所示，数轴上O，A两点的距离为8，一动点P从点A出发，按以下规律跳动：第1次跳动到AO的中点A1处，第2次从A1点跳动到A1O的中点A2处，第3次从A2点跳动到A2O的中点A3处，按照这样的规律继续跳动到点A4，A5，A6，…，An（n≥3，n是整数）处，问经过这样2023次跳动后的点与A1A的中点的距离是（　　）

A． B． C． D．

二、填空题（本题共4个小题；每个小题3分，共12分，把正确答案填在横线上）

15．（2022·广东·深圳市文锦中学七年级期中）将一个长，宽的长方形绕它的长边所在的直线旋转一周，所得几何体的体积为______.

16．（2021·湖北·十堰市郧阳区教学研究室七年级期末）已知∠与∠β互余，且∠＝，则∠β＝________．

17．（2022·山西·右玉县第三中学校七年级期末）一条直线上有，，三点，，，点，分别是，的中点，则______．

18．（2022·河南·商丘市第十六中学七年级期末）如图，有一种电子游戏，电子屏幕上有一条直线，在直线上有A，B，C，D四点．点P沿直线l从右向左移动，当出现点P与A，B，C，D四点中的至少两个点距离相等时，就会发出警报，则直线l上会发出警报的点P最多有____________个．

三、解答题（本题共8道题，19-21每题6分，22-25每题8分，26题10分，满分60分）

19．（2022·江苏·七年级专题练习）如图所示，有一个正方体，棱长为，如果在它的左上方截去一个长、宽、高分别为，，的长方体，求它的表面积减少了百分之几？

20．（2021·山东威海·期中）如图是一个长方体墨水纸盒的平面展开图，纸盒中相对两个面上的数互为相反数．

(1)填空：a= _______   b= _______ c= _______；

(2)求的值．

21．（2022·河北邢台·七年级期末）如图，在同一个平面内有四个点，请用直尺和圆规按下列要求作图（不写作图步骤，保留作图痕迹），

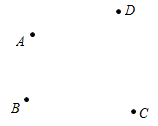
(1)作射线AB；

(2)作直线AC与直线BD相交于点O；

(3)在射线AB上作线段，使线段与线段AC相等

22．（2022·黑龙江·大庆市庆新中学期末）如图所示，∠AOB=100°，OC是∠AOB内部的一条射线，射线OM平分∠AOC，射线ON 平分∠BOC，求∠MON的度数．

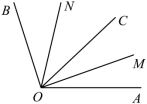
解：因为射线       ，      分别平分∠        和∠        ，

所以∠NOB=∠NOC=      ∠BOC，∠AOM=∠COM=      ∠AOC，

所以∠MON=∠      +∠      =                  =        =          °

23．（2022·新疆·乌市八中七年级期中）如图，延长线段到，使，点是线段的中点，如果，

(1)求的长度；

(2)若点是线段的中点，求的长度．

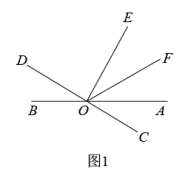
24．（2021·全国·七年级专题练习）直线AB、CD相交于点O，∠EOF在∠AOD的内部．

（1）如图1，当∠AOD＝150°，∠EOF＝30°时，求∠AOF与∠EOD的度数和；

（2）在（1）的条件下，请直接写出图中与∠BOC互补的角；

（3）如图2，若射线OM平分∠AOD（OM在∠EOD内部），且满足∠EOD＝2∠FOM，请判断∠AOF与∠EOF的大小关系并说明理由．

25．（2021·湖北·十堰市郧阳区教学研究室七年级期末）如图，已知线段，动点P从A出发，以每秒2个单位的速度沿射线方向运动，运动时间为t秒（），点M为的中点．

(1)若点P在线段上运动，当t为多少时，？

(2)若点P在射线上运动，N为线段上的一点．

①当N为的中点时，求线段的长度；

②当时，是否存在这样的t，使M，N，P三点中的一个点是以其余两点为端点的线段的中点？如果存在，请求出t的值；如不存在，请说明理由．

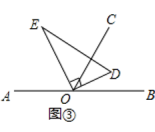
26．（2021·山东淄博·期中）如图，以直线上一点为端点作射线，使，将一个直角三角形的直角顶点放在点处．（注：

(1)如图①，若直角三角板的一边放在射线上，则　　；

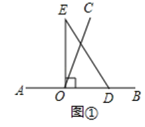
(2)如图②，将直角三角板绕点逆时针方向转动到某个位置，若恰好平分，求的度数；

(3)如图③，将直角三角板绕点转动，如果始终在的内部，试猜想和有怎样的数量关系？并说明理由．