
北师大版八年级上册3 勾股定理的应用精练
展开
这是一份北师大版八年级上册3 勾股定理的应用精练,共9页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
![]() 1.3勾股定理的应用同步练习-2023-2024学年北师大版数学八年级上册学校:___________姓名:___________班级:___________考号:___________ 一、单选题1.如图,圆柱形玻璃杯高为
1.3勾股定理的应用同步练习-2023-2024学年北师大版数学八年级上册学校:___________姓名:___________班级:___________考号:___________ 一、单选题1.如图,圆柱形玻璃杯高为![]() ,底面周长为
,底面周长为![]() ,在杯内壁离杯底
,在杯内壁离杯底![]() 的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿
的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿![]() 且与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为( )
且与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为( )![]() .(杯壁厚度不计)
.(杯壁厚度不计)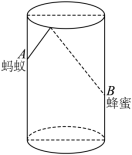 A.20 B.25 C.30 D.402.如图,一个底面圆周长为24cm,高为9cm的圆柱体,一只蚂蚁从距离上边缘4cm的点A沿侧面爬行到相对的底面上的点B所经过的最短路线长为( )
A.20 B.25 C.30 D.402.如图,一个底面圆周长为24cm,高为9cm的圆柱体,一只蚂蚁从距离上边缘4cm的点A沿侧面爬行到相对的底面上的点B所经过的最短路线长为( )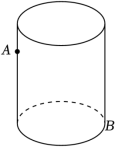 A.
A.![]() B.15cm C.14cm D.13cm3.固定在地面上的一个正方体木块(如图①),其棱长为
B.15cm C.14cm D.13cm3.固定在地面上的一个正方体木块(如图①),其棱长为![]() ,沿其相邻三个面的对角线(图中虚线)去掉一角,得到如图②所示的几何体木块,一只蚂蚁沿着该木块的表面从点A爬行到点B的最短路程为( )
,沿其相邻三个面的对角线(图中虚线)去掉一角,得到如图②所示的几何体木块,一只蚂蚁沿着该木块的表面从点A爬行到点B的最短路程为( )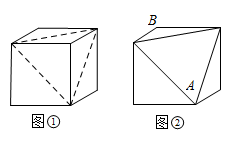 A.
A.![]() B.
B.![]() C.
C.![]() D.
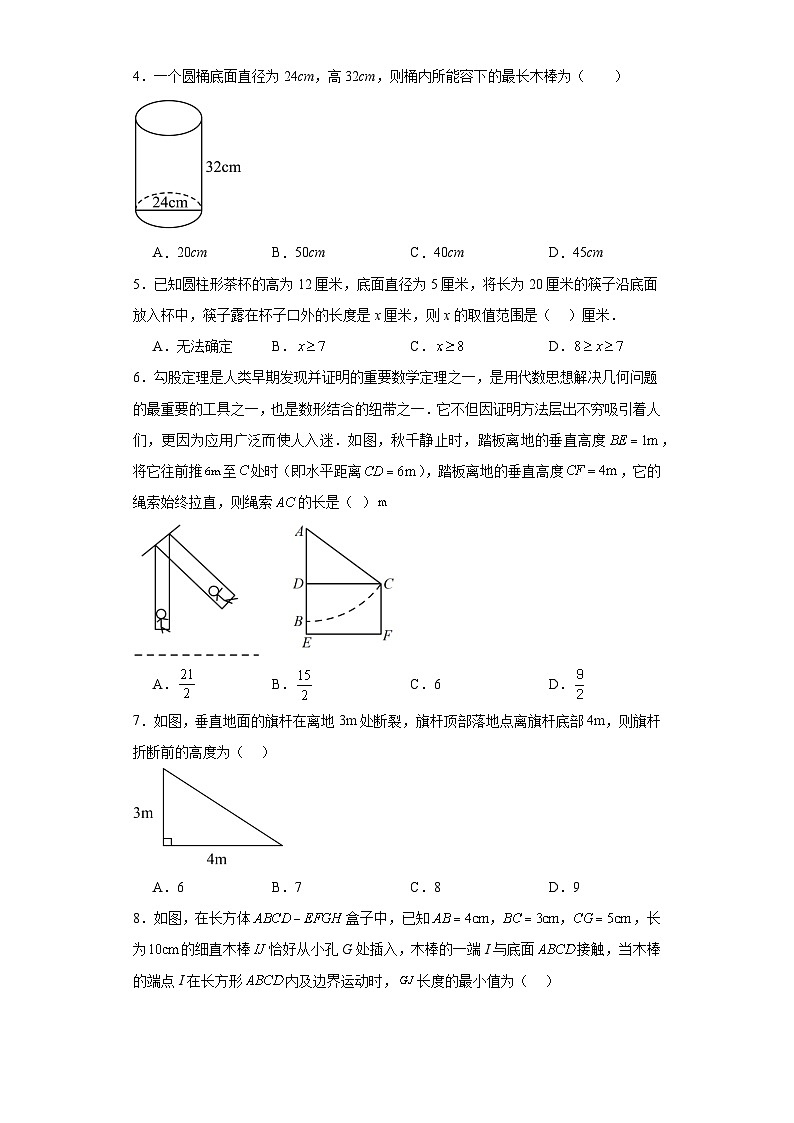
D.![]() 4.一个圆桶底面直径为24cm,高32cm,则桶内所能容下的最长木棒为( )
4.一个圆桶底面直径为24cm,高32cm,则桶内所能容下的最长木棒为( )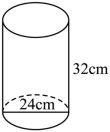 A.20cm B.50cm C.40cm D.45cm5.已知圆柱形茶杯的高为12厘米,底面直径为5厘米,将长为20厘米的筷子沿底面放入杯中,筷子露在杯子口外的长度是x厘米,则x的取值范围是( )厘米.A.无法确定 B.
A.20cm B.50cm C.40cm D.45cm5.已知圆柱形茶杯的高为12厘米,底面直径为5厘米,将长为20厘米的筷子沿底面放入杯中,筷子露在杯子口外的长度是x厘米,则x的取值范围是( )厘米.A.无法确定 B.![]() C.
C.![]() D.
D.![]() 6.勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一.它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.如图,秋千静止时,踏板离地的垂直高度
6.勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一.它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.如图,秋千静止时,踏板离地的垂直高度![]() ,将它往前推
,将它往前推![]() 至
至![]() 处时(即水平距离
处时(即水平距离![]() ),踏板离地的垂直高度
),踏板离地的垂直高度![]() ,它的绳索始终拉直,则绳索
,它的绳索始终拉直,则绳索![]() 的长是( )
的长是( )![]()
 A.
A.![]() B.
B.![]() C.6 D.
C.6 D.![]() 7.如图,垂直地面的旗杆在离地3m处断裂,旗杆顶部落地点离旗杆底部4m,则旗杆折断前的高度为( )
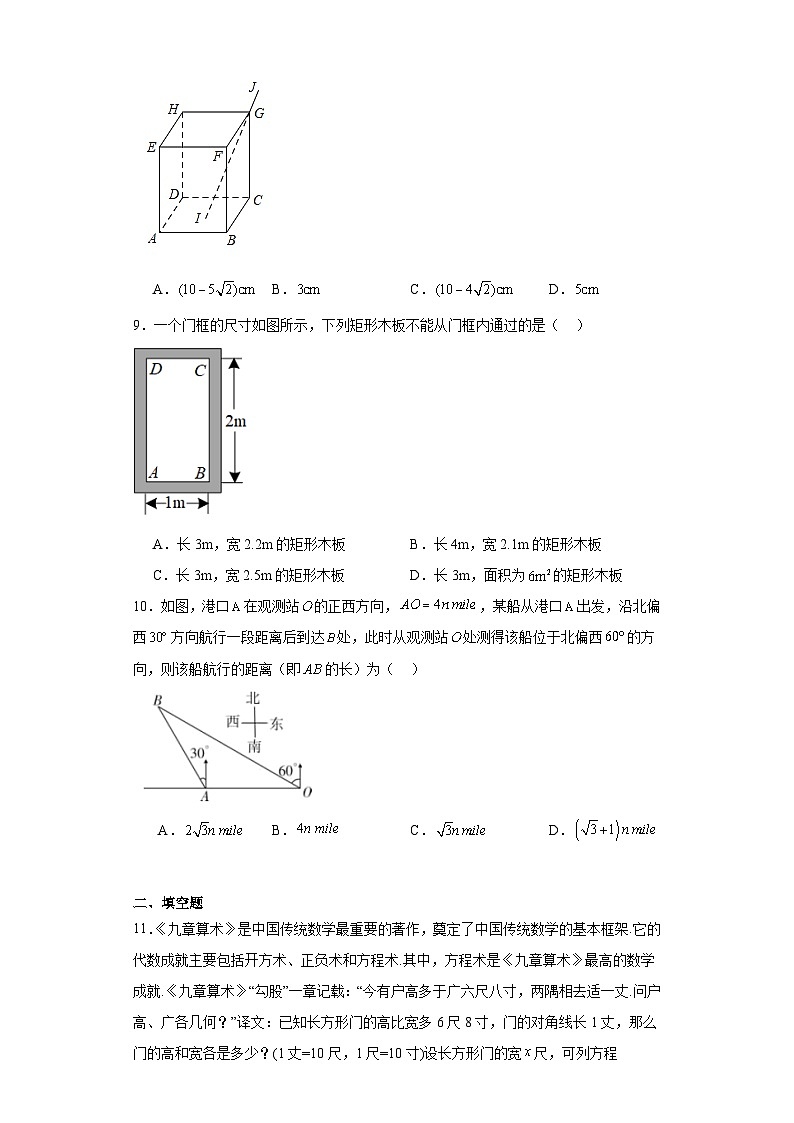
7.如图,垂直地面的旗杆在离地3m处断裂,旗杆顶部落地点离旗杆底部4m,则旗杆折断前的高度为( )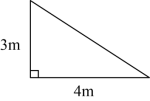 A.6 B.7 C.8 D.98.如图,在长方体
A.6 B.7 C.8 D.98.如图,在长方体![]() 盒子中,已知
盒子中,已知![]() ,长为
,长为![]() 的细直木棒
的细直木棒![]() 恰好从小孔G处插入,木棒的一端I与底面
恰好从小孔G处插入,木棒的一端I与底面![]() 接触,当木棒的端点I在长方形
接触,当木棒的端点I在长方形![]() 内及边界运动时,
内及边界运动时,![]() 长度的最小值为( )
长度的最小值为( )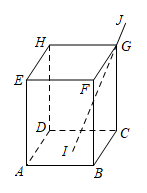 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.一个门框的尺寸如图所示,下列矩形木板不能从门框内通过的是( )
9.一个门框的尺寸如图所示,下列矩形木板不能从门框内通过的是( )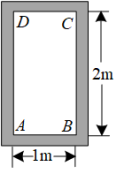 A.长3m,宽2.2m的矩形木板 B.长4m,宽2.1m的矩形木板C.长3m,宽2.5m的矩形木板 D.长3m,面积为
A.长3m,宽2.2m的矩形木板 B.长4m,宽2.1m的矩形木板C.长3m,宽2.5m的矩形木板 D.长3m,面积为![]() 的矩形木板10.如图,港口
的矩形木板10.如图,港口![]() 在观测站
在观测站![]() 的正西方向,
的正西方向,![]() ,某船从港口
,某船从港口![]() 出发,沿北偏西
出发,沿北偏西![]() 方向航行一段距离后到达
方向航行一段距离后到达![]() 处,此时从观测站
处,此时从观测站![]() 处测得该船位于北偏西
处测得该船位于北偏西![]() 的方向,则该船航行的距离(即
的方向,则该船航行的距离(即![]() 的长)为( )
的长)为( )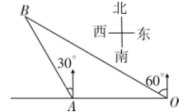 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题11.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》“勾股”一章记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”译文:已知长方形门的高比宽多6尺8寸,门的对角线长1丈,那么门的高和宽各是多少?(1丈=10尺,1尺=10寸)设长方形门的宽
二、填空题11.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》“勾股”一章记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”译文:已知长方形门的高比宽多6尺8寸,门的对角线长1丈,那么门的高和宽各是多少?(1丈=10尺,1尺=10寸)设长方形门的宽![]() 尺,可列方程为 .
尺,可列方程为 . 12.某工程队负责挖掘一处通山隧道,为了保证山脚A,B两处出口能够直通,工程队在工程图上留下了一些测量数据(此为山体俯视图,图中测量线拐点处均为直角,数据单位:米).据此可以求得该隧道预计全长 米.
12.某工程队负责挖掘一处通山隧道,为了保证山脚A,B两处出口能够直通,工程队在工程图上留下了一些测量数据(此为山体俯视图,图中测量线拐点处均为直角,数据单位:米).据此可以求得该隧道预计全长 米.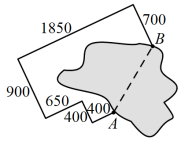 13.有—个长为12cm,宽为
13.有—个长为12cm,宽为![]() ,高为3cm的长方形铁盒,在其内部要放一根笔直的铅笔,则铅笔长度不应超过
,高为3cm的长方形铁盒,在其内部要放一根笔直的铅笔,则铅笔长度不应超过 ![]() .14.如图,甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B.若A,B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向是 .
.14.如图,甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B.若A,B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向是 . 15.如图,在矩形ABCD中,AB=5,AD=3,动点P满足3S△PAB=S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为 .
15.如图,在矩形ABCD中,AB=5,AD=3,动点P满足3S△PAB=S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为 .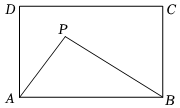 16.如图,一架长为4m的梯子,一端放在离墙脚2.4m处,另一端靠墙,则梯子顶端离墙脚 m.
16.如图,一架长为4m的梯子,一端放在离墙脚2.4m处,另一端靠墙,则梯子顶端离墙脚 m.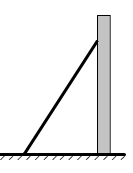 17.一只蚂蚁从圆柱体的下底面A点沿着侧面爬到上底面B点,已知圆柱的底面周长为12cm,高为8cm,则蚂蚁所走过的最短路径是 cm.
17.一只蚂蚁从圆柱体的下底面A点沿着侧面爬到上底面B点,已知圆柱的底面周长为12cm,高为8cm,则蚂蚁所走过的最短路径是 cm.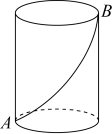 18.如图,在东西走向的铁路上有A、B两站(视为直线上的两点)相距36千米,在A、B的正北分别有C、D两个蔬菜基地,其中C到A站的距离为24千米,D到B站的距离为12千米,现要在铁路AB上建一个蔬菜加工厂E,使蔬菜基地C、D到E的距离相等,则E站应建在距A站 千米的地方.
18.如图,在东西走向的铁路上有A、B两站(视为直线上的两点)相距36千米,在A、B的正北分别有C、D两个蔬菜基地,其中C到A站的距离为24千米,D到B站的距离为12千米,现要在铁路AB上建一个蔬菜加工厂E,使蔬菜基地C、D到E的距离相等,则E站应建在距A站 千米的地方.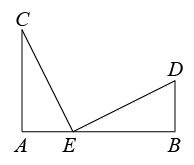 19.如下图是一只圆柱形玻璃杯,杯高为
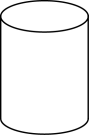
19.如下图是一只圆柱形玻璃杯,杯高为![]() ,将一根筷子插入其中,留在杯外最长
,将一根筷子插入其中,留在杯外最长![]() ,最短
,最短![]() ,则这只玻璃杯的内径是
,则这只玻璃杯的内径是 ![]() .
. 20.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,在
20.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.如果设
的长.如果设![]() ,则可列方程为 .
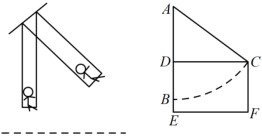
,则可列方程为 .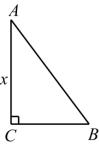 三、解答题21.小明是一名升旗手,面对高高的旗杆,他想出了好几种方法测量方法,学过直角三角形后,他只用一把卷尺就测出了旗杆
三、解答题21.小明是一名升旗手,面对高高的旗杆,他想出了好几种方法测量方法,学过直角三角形后,他只用一把卷尺就测出了旗杆![]() 的高度.下面是他测量的过程和数据:第一步:测得从旗杆顶端垂直挂下来的升旗用的绳子比旗杆长1m(如图1),第二步:拉着绳子的下端往后退,当他将绳子拉直时,测得此时拉绳子的手到地面的距离
的高度.下面是他测量的过程和数据:第一步:测得从旗杆顶端垂直挂下来的升旗用的绳子比旗杆长1m(如图1),第二步:拉着绳子的下端往后退,当他将绳子拉直时,测得此时拉绳子的手到地面的距离![]() 为1m,到旗杆的距离
为1m,到旗杆的距离![]() 为8m,(如图2).他很快算出了旗杆的高度,请你也来试一试.
为8m,(如图2).他很快算出了旗杆的高度,请你也来试一试.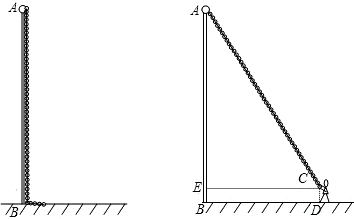 22.如图,有一空心圆柱,高为
22.如图,有一空心圆柱,高为![]() ,底面周长为
,底面周长为![]() ,在圆柱内的下底面A处有一只蝴蝶,它想和上底面B处的同伴汇合,则这只蝴蝶经过的最短距离是多少
,在圆柱内的下底面A处有一只蝴蝶,它想和上底面B处的同伴汇合,则这只蝴蝶经过的最短距离是多少![]() ?(
?(![]() 取3)
取3) 23.“三农”问题是关系国计民生的根本问题,实施乡村振兴战略是建设美丽中国的关键举措.如图,公路上
23.“三农”问题是关系国计民生的根本问题,实施乡村振兴战略是建设美丽中国的关键举措.如图,公路上![]() 两点相距50km,
两点相距50km,![]() 为两村庄,
为两村庄,![]() 于
于![]() ,
,![]() 于
于![]() ,已知
,已知![]() ,
,![]() ,现在要在公路
,现在要在公路![]() 上建一个土特产品市场
上建一个土特产品市场![]() ,使得
,使得![]() 两村庄到市场
两村庄到市场![]() 的距离相等,则市场
的距离相等,则市场![]() 应建在距
应建在距![]() 多少千米处?并判断此时
多少千米处?并判断此时![]() 的形状,请说明理由.
的形状,请说明理由.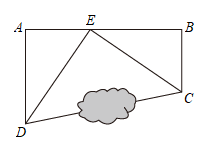 24.如图,在笔直的铁路上A,B两点相距20km,C,D为两村庄,DA=8km,CB=14km,DA⊥AB于点A,CB⊥AB于点B.现要在AB上建一个中转站E,使得C,D两村到E站的距离相等,求AE的长.
24.如图,在笔直的铁路上A,B两点相距20km,C,D为两村庄,DA=8km,CB=14km,DA⊥AB于点A,CB⊥AB于点B.现要在AB上建一个中转站E,使得C,D两村到E站的距离相等,求AE的长.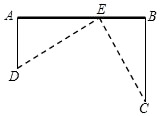 25.如图,将长为25米长的云梯
25.如图,将长为25米长的云梯![]() 斜靠在建筑物的侧墙上,
斜靠在建筑物的侧墙上,![]() 长7米.
长7米.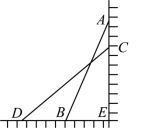 (1)求梯子上端到墙的底端E的距离
(1)求梯子上端到墙的底端E的距离![]() 的长;(2)如果梯子的顶端A沿墙下滑4米,则梯脚B将外移多少米?
的长;(2)如果梯子的顶端A沿墙下滑4米,则梯脚B将外移多少米?
参考答案:1.B2.D3.A4.C5.D6.B7.C8.A9.C10.B11.![]() 12.100013.1314.北偏西60°15.
12.100013.1314.北偏西60°15.![]() 16.3.217.
16.3.217.![]() 18.1219.720.
18.1219.720.![]() 21.1622.
21.1622.![]() 23.市场
23.市场![]() 应建在距
应建在距![]() 的20千米处;
的20千米处;![]() 是等腰直角三角形.24.13.3km25.(1)
是等腰直角三角形.24.13.3km25.(1)![]() 的长
的长![]() 米;(2)梯脚B将外移8米.
米;(2)梯脚B将外移8米.
相关试卷
这是一份初中数学北师大版八年级上册3 勾股定理的应用当堂检测题,共8页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份北师大版八年级上册3 勾股定理的应用当堂达标检测题,共8页。试卷主要包含了单选题,填空题,应用题等内容,欢迎下载使用。
这是一份初中数学北师大版八年级上册3 勾股定理的应用同步测试题,共7页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。









