2023年山东省济宁市梁山县中考数学二模试卷（含解析）

这是一份2023年山东省济宁市梁山县中考数学二模试卷（含解析），共20页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。
2023年山东省济宁市梁山县中考数学二模试卷
一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）
1. −2023的倒数是(    )
A. −2023 B. 2023 C. −12023 D. 12023
2. 中国互联网络信息中心近期发布第51次《中国互联网络发展状况统计报告》显示，截止到2022年12月，我国网民规模达10.67亿.将数据10.67亿用科学记数法表示为(    )
A. 1.067×108 B. 10.67×108 C. 1.067×109 D. 0.1067×1010
3. 下列计算正确的是(    )
A. (−a2b3)3=−a6b6 B. (2−a)2=4−a2
C. a3⋅a4=a7 D. 8− 2= 6
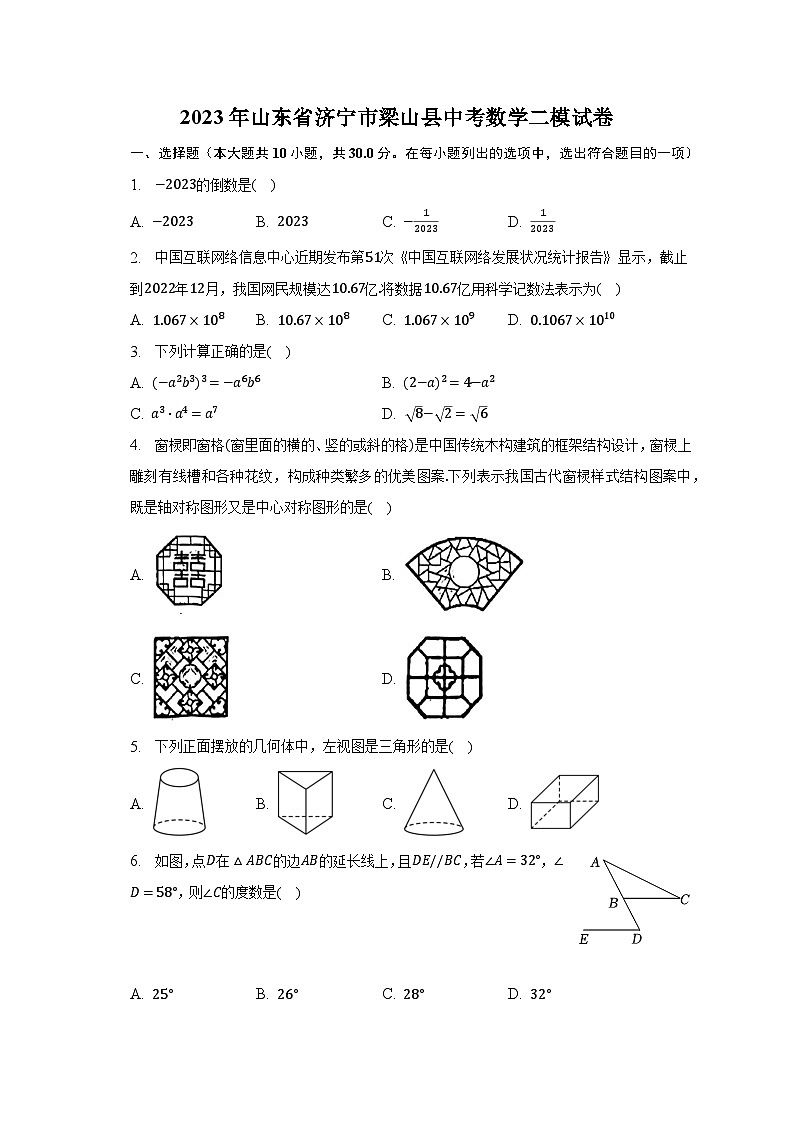
4. 窗棂即窗格(窗里面的横的、竖的或斜的格)是中国传统木构建筑的框架结构设计，窗棂上雕刻有线槽和各种花纹，构成种类繁多的优美图案.下列表示我国古代窗棂样式结构图案中，既是轴对称图形又是中心对称图形的是(    )
A. B.
C. D.
5. 下列正面摆放的几何体中，左视图是三角形的是(    )
A. B. C. D.
6. 如图，点D在△ABC的边AB的延长线上，且DE//BC，若∠A=32°，∠D=58°，则∠C的度数是(    )


A. 25° B. 26° C. 28° D. 32°
7. 如图，CD，CE，CF分别是△ABC的高、角平分线、中线，则下列各式中错误的是(    )

A. AB=2BF B. ∠ACE=12∠ACB
C. AE=BE D. CD⊥BE
8. 习近平总书记指出，中华优秀传统文化是中华民族的“根”和“魂”.为了大力弘扬中华优秀传统文化，某校决定开展名著阅读活动．用3600元购买“四大名著”若干套后，发现这批图书满足不了学生的阅读需求，图书管理员在购买第二批时正赶上图书城八折销售该套书，于是用2400元购买的套数只比第有批少4套．设第一批购买的“四大名著”每套的价格为x元，则符合题意的方程是(    )
A. 36000.8x−3600x=4 B. 3600x−24000.8x=4
C. 24000.8x−3600x=0 D. 24000.8x−2400x=4
9. 如图，AB为⊙O的直径，点C在⊙O上，且CO⊥AB于点O，弦CD与AB相交于点E，连接AD，若∠A=19°，则∠AEC的度数为(    )
A. 19°
B. 21°
C. 26°
D. 64°
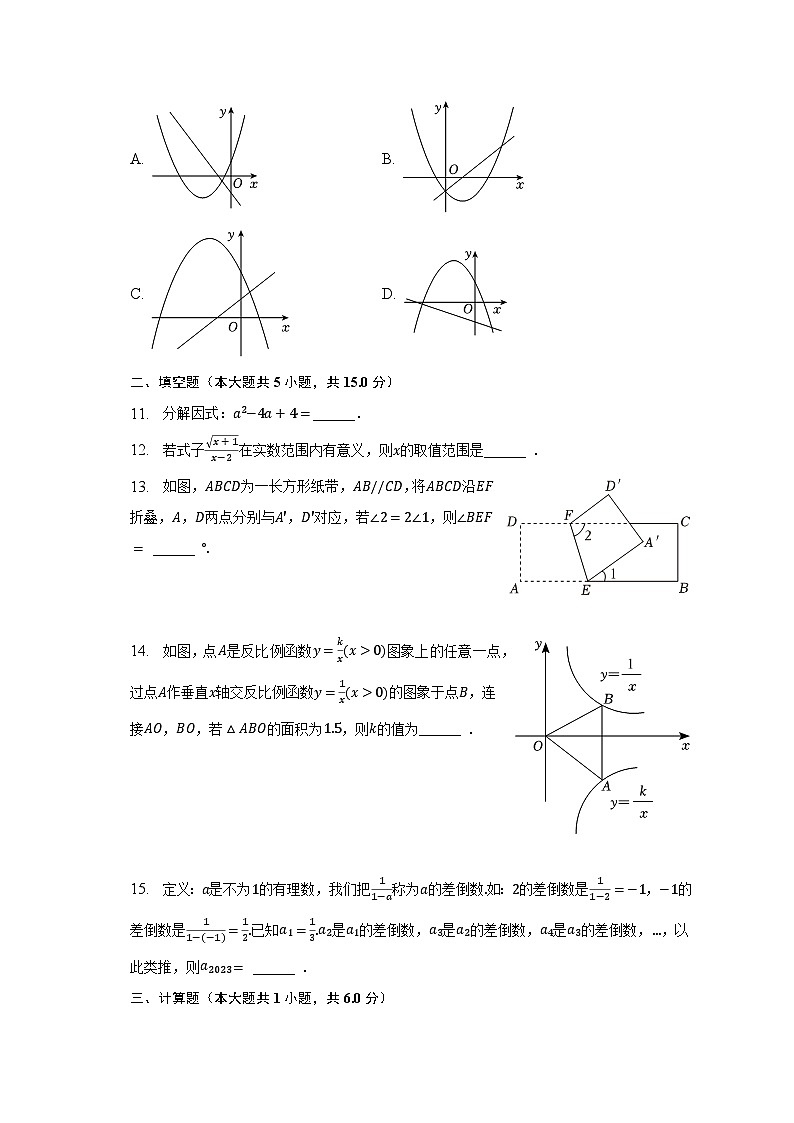
10. 在同一平面直角坐标系中，二次函数y=ax2−4x+c2(a≠0)与一次函数y=4x−c的图象可能是(    )
A. B.
C. D.
二、填空题（本大题共5小题，共15.0分）
11. 分解因式：a2−4a+4=______．
12. 若式子 x+1x−2在实数范围内有意义，则x的取值范围是______ ．
13. 如图，ABCD为一长方形纸带，AB//CD，将ABCD沿EF折叠，A，D两点分别与A′，D′对应，若∠2=2∠1，则∠BEF= ______ °.


14. 如图，点A是反比例函数y=kx(x>0)图象上的任意一点，过点A作垂直x轴交反比例函数y=1x(x>0)的图象于点B，连接AO，BO，若△ABO的面积为1.5，则k的值为______ ．


15. 定义：a是不为1的有理数，我们把11−a称为a的差倒数.如：2的差倒数是11−2=−1，−1的差倒数是11−(−1)=12.已知a1=13.a2是a1的差倒数，a3是a2的差倒数，a4是a3的差倒数，…，以此类推，则a2023= ______ ．
三、计算题（本大题共1小题，共6.0分）
16. 计算：(π−1)0+4sin45°− 8+|−3|．
四、解答题（本大题共6小题，共49.0分。解答应写出文字说明，证明过程或演算步骤）
17. (本小题6.0分)
以“赏中华诗词、寻文化基因，品生活之美”为基本宗旨的《中国诗词大会》是央视首档全民参与的诗词节目.某语文科组对本校学生了解《中国诗词大会》的情况进行调查，随机选取部分学生进行问卷调查，问卷设有4个选项(每位被调查的学生必选且只选一项)：A.几乎每期都看；B.看过几期；C.听说过，但没看过；D.没听说过，现绘制了如图的条形统计图和扇形统计图，请结合统计图回答下列问题：

(1)本次共问卷调查______ 名学生：扇形统计图中，B选项对应的扇形圆心角是______ 度.
(2)补全图中的条形统计图．
(3)该校选“A”的学生中有甲、乙、丙三人最关注该节目，学校决定从这三名学生中随机抽取两名为该节目作宣传，用列表法或画树状图法求同时抽到甲、乙两名学生的概率．
18. (本小题7.0分)
定义：若一元二次方程ax2+bx+c=0(a≠0)满足b=a+c.则称该方程为“和谐方程”．
(1)下列属于和谐方程的是______；
①x2+2x+1=0；②x2−2x+1=0；③x2+x=0．
(2)求证：和谐方程总有实数根；
(3)已知：一元二次方程ax2+bx+c=0(a≠0)为“和谐方程”，若该方程有两个相等的实数根，求a，c的数量关系．
19. (本小题9.0分)
某商场试销一款玩具，进价为20元/件，商场与供货商约定，试销期间利润不高于30%，且同一周内售价不变.从试销记录看到，当售价为22元时，一周销售了80件该玩具；当售价为24元时，一周销售了60件该玩具.每周销量y(件)与售价x(元)符合一次函数关系．
(1)求每周销量y(件)与售价x(元)之间的关系式；
(2)若商场一周内销售该玩具获得的利润为210元，则该玩具的售价为多少元？
(3)商场将该玩具的售价定为多少时，一周内销售该玩具获得利润最大？最大利润W为多少元？
20. (本小题8.0分)
如图，AB是⊙O的直径，C，D都是⊙O上的点，AD平分∠CAB，过点D作AC的垂线交AC的延长线于点E，交AB的延长线于点F．
(1)求证：EF是⊙O的切线；
(2)若AB=10，AC=6，求CE的值．

21. (本小题9.0分)
定义：从三角形(不是等腰三角形)的一个顶点引出一条射线与对边相交，顶点与交点所连线段把这个三角形分割成两个小三角形，如果其中一个为等腰三角形，另一个与原三角形相似，我们就把这条线段叫做这个三角形的“华丽分割线”．
例如：如图1，AD把△ABC分成△ABD和△ADC，若△ABD是等腰三角形，且△ADC∽△BAC，那么AD就是△ABC的“华丽分割线”．
(1)【定义感知】
如图1，在△ABC中，∠B=40°，∠BAC=110°，AB=BD．
求证：AD是△ABC的“华丽分割线”．
(2)【问题解决】
①如图2，在△ABC中，∠B=46°，AD是△ABC的“华丽分割线”，且△ABD是等腰三角形，则∠C的度数为______ ．
②如图3，在△ABC中，AB=2，AC= 3，AD是△ABC的“华丽分割线”，且△ABD是以AD为底边的等腰三角形，求华丽分割线AD的长．


22. (本小题10.0分)
在平面直角坐标系中，抛物线y=−x2−4x+c与x轴交于点A，B(点A在点B的左侧)，与y轴交于点C，且点A的坐标为(−5,0)．

(1)求点C的坐标；
(2)如图1，若点P是第二象限内抛物线上一动点，求点P到直线AC距离的最大值；
(3)如图2，若点M是抛物线上一点，点N是抛物线对称轴上一点，是否存在点M使以A，C，M，N为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由．
答案和解析

1.【答案】C 
【解析】解：−2023的倒数是−12023．
故选：C．
根据相乘等于1的两个数互为倒数，即可求解．
本题考查了倒数，掌握倒数的定义是解题的关键．

2.【答案】C 
【解析】解：10.67亿=1067000000=1.067×109，
故选：C．
将一个数表示成a×10n，其中1≤|a|0，对称轴为直线x=−−42a=2a>0，故A选项不合题意；
当抛物线开口向下，则a