
2023年中考数学 章节专项练习41 统计图表
展开一、选择题
1. (2019四川巴中,7,4分)如图所示,是巴中某校对学生到校方式的情况统计图,若该校骑自行车到校的学生有200人,则步行到校的学生有( )
A.120人 B.160人 C.125人 D.180人
第7题图
【答案】B
【解析】因为该校骑自行车到校的学生有200人,占比25%,所以可得全校总人数为200÷25%=800(人),步行人数占比20%,故人数为800×20%=160(人),故选B
【知识点】扇形统计图,百分比
二、解答题
1.(2019浙江台州,21,10分)安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害,为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽取了部分使用电瓶车的市民,就骑电瓶车戴安全帽情况进行问卷调查,将手机的数据制成如下统计图表.
活动前骑电瓶车戴安全帽情况统计表
类别
人数
A
68
B
245
C
510
D
177
合计
1000
A:每次戴
B:经常戴
C:偶尔戴
D:都不戴
第21题图
(1)宣传活动前,在抽取的市民中哪一类别的人数最多?占抽取人数的百分之几?
(2)该市约有30万人使用电瓶车,请估计活动前全市骑电瓶车"都不戴"安全帽的总人数;
(3)小明认为,宣传活动后骑电瓶车"都不戴"安全帽的人数为178,比活动前增加了1人,因此交警部门开展的宣传活动没有效果.小明分析数据的方法是否合理?请结合统计图表,对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法.
【思路分析】(1)比较大小可得C类最多,进而求出所占百分比;(2)根据样本百分比估计总体中"都不戴"的人数;(3)作出结论应该比较占比大小,不能单纯比较数量得到结论.
【解题过程】(1)由表格数据可知,C类偶尔戴的市民人数最多,占比为:=51%.
(2)(人),答:活动前全市骑电瓶车"都不戴"安全帽的总人数为53100人.
(3)不合理.∵活动开始前后调查的总人数不同,要比较所占百分比大小才能得到正确结论.活动开展前,"都不戴"占比为,活动开展后,"都不戴"占比为,∵17.7%>8.9%,所占百分比下降,"每次戴"的比例有6.8%大幅度上升到44.8%,说明活动有效果.
【知识点】统计图,统计表,百分比及应用,样本估计总体
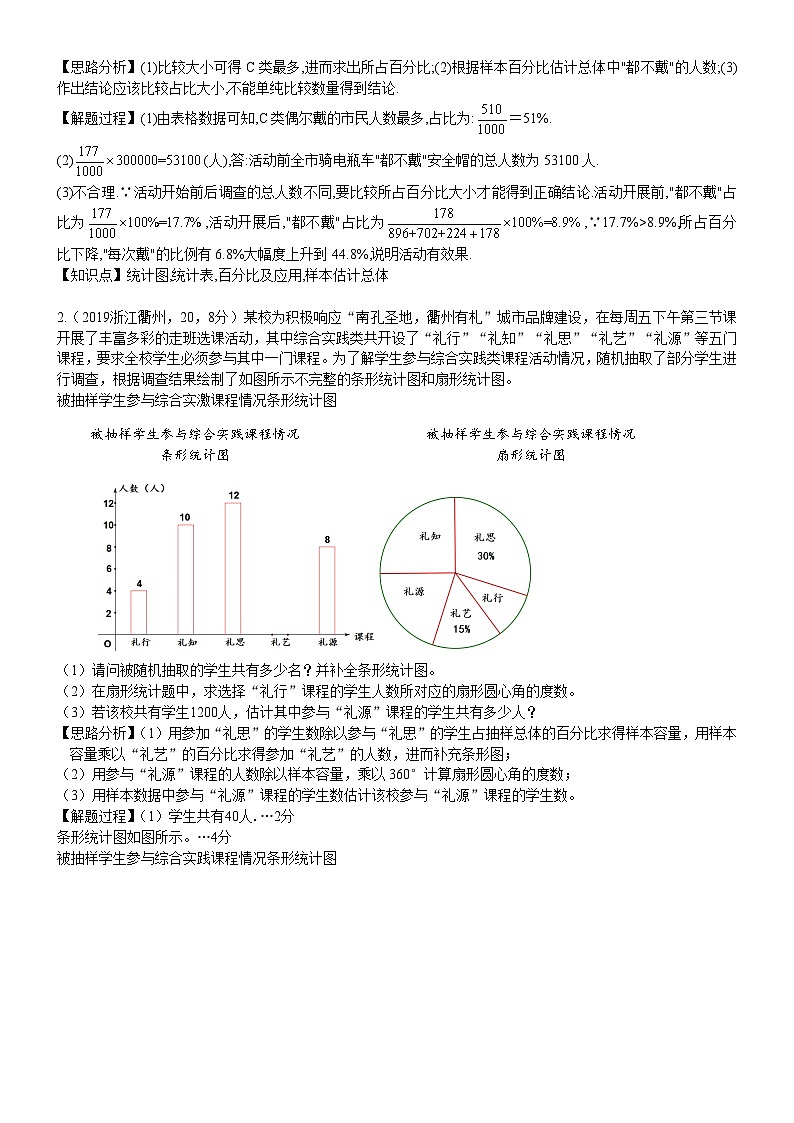
2.(2019浙江衢州,20,8分)某校为积极响应“南孔圣地,衢州有札”城市品牌建设,在每周五下午第三节课开展了丰富多彩的走班选课活动,其中综合实践类共开设了“礼行”“礼知”“礼思”“礼艺”“礼源”等五门课程,要求全校学生必须参与其中一门课程。为了解学生参与综合实践类课程活动情况,随机抽取了部分学生进行调查,根据调查结果绘制了如图所示不完整的条形统计图和扇形统计图。
被抽样学生参与综合实激课程情况条形统计图
被抽样学生参与综合实践课程情况
条形统计图
被抽样学生参与综合实践课程情况
扇形统计图
(1)请问被随机抽取的学生共有多少名?并补全条形统计图。
(2)在扇形统计题中,求选择“礼行”课程的学生人数所对应的扇形圆心角的度数。
(3)若该校共有学生1200人,估计其中参与“礼源”课程的学生共有多少人?
【思路分析】(1)用参加“礼思”的学生数除以参与“礼思”的学生占抽样总体的百分比求得样本容量,用样本容量乘以“礼艺”的百分比求得参加“礼艺”的人数,进而补充条形图;
(2)用参与“礼源”课程的人数除以样本容量,乘以360°计算扇形圆心角的度数;
(3)用样本数据中参与“礼源”课程的学生数估计该校参与“礼源”课程的学生数。
【解题过程】(1)学生共有40人.…2分
条形统计图如图所示。…4分
被抽样学生参与综合实践课程情况条形统计图
(2)选“礼行“课程的学生所对应的扇形圆心角的度数为×360°=36°.…6分
(3)参与“礼源”课程的学生约有1200×=240(人).…8分。
【知识点】条形统计图扇形统计图用样本估计总体
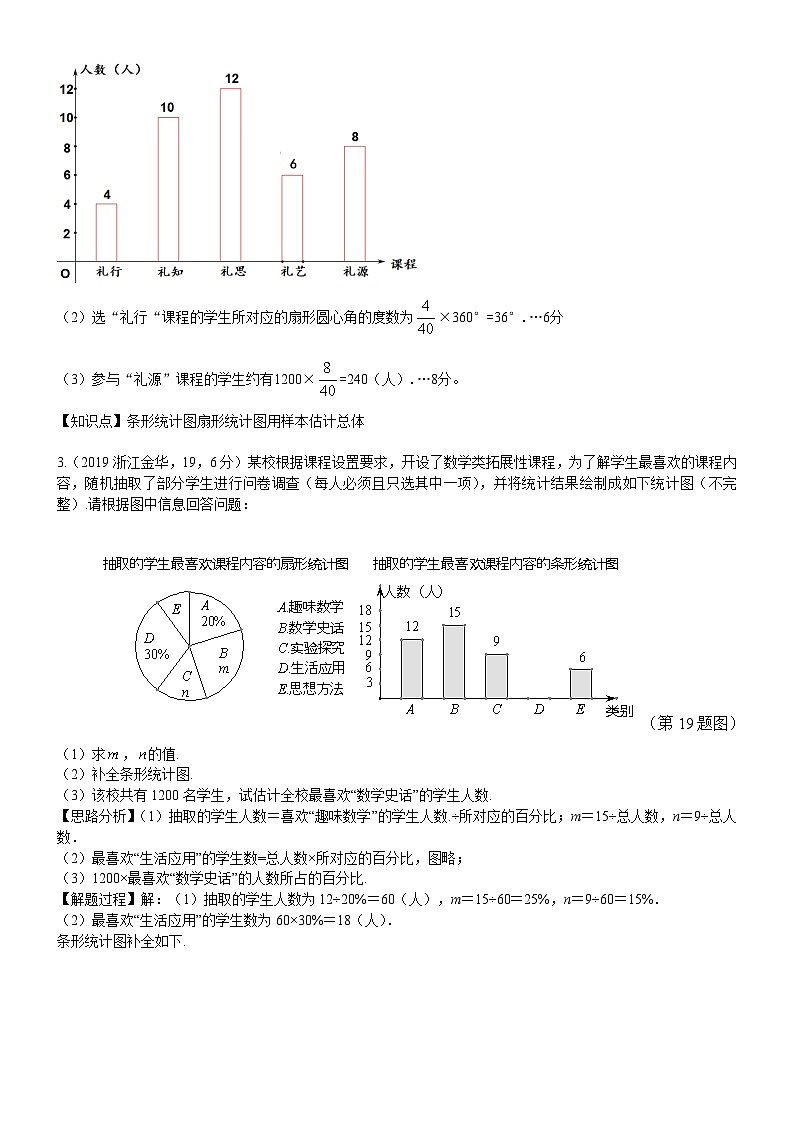
3.(2019浙江金华,19,6分)某校根据课程设置要求,开设了数学类拓展性课程,为了解学生最喜欢的课程内容,随机抽取了部分学生进行问卷调查(每人必须且只选其中一项),并将统计结果绘制成如下统计图(不完整).请根据图中信息回答问题:
(第19题图)
(1)求,的值.
(2)补全条形统计图.
(3)该校共有1200名学生,试估计全校最喜欢“数学史话”的学生人数.
【思路分析】(1)抽取的学生人数=喜欢“趣味数学”的学生人数.÷所对应的百分比;m=15÷总人数,n=9÷总人数.
(2)最喜欢“生活应用”的学生数=总人数×所对应的百分比,图略;
(3)1200×最喜欢“数学史话”的人数所占的百分比.
【解题过程】解:(1)抽取的学生人数为12÷20%=60(人),m=15÷60=25%,n=9÷60=15%.
(2)最喜欢“生活应用”的学生数为60×30%=18(人).
条形统计图补全如下.
(3)该校共有1200名学生,估计全校最喜欢“数学史话”的学生有1200×25%=300(人).
【知识点】条形统计图;扇形统计图
4.(2019山东省淄博市,20,8分)文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年3月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别
年龄段
频数(人数)
第1组
10≤x<20
5
第2组
20≤x<30
a
第3组
30≤x<40
35
第4组
40≤x<50
20
第5组
50≤x<60
15
(1)请直接写出a=_________,m=_________,第3组人数在扇形统计图中所对应的圆心角是________度;
(2)请补全上面的频数分布直方图;
(3)假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?
【思路分析】
【解题过程】(1)a=100-5-35-20-15=25;m%=20÷100=20%,∴m=20;圆心角=×360°=126°.
(2)a=25人,
(3)×300万=60万.
【知识点】频数,直方图,扇形统计图,
5.(2019山东泰安,20,8分)为弘扬泰山文化,某校举办了”泰山诗文大赛”活动,从中随机抽取部分学生的比赛成绩,根据成绩(成绩都高于50分),绘制了如下的统计图表(不完整):
组别
分数
人数
第1组
90
第2组
80
第3组
70
第4组
60
第5组
50
第20题图
请根据以上信息,解答下列问题:
(1)求出a,b的值;
(2)计算扇形统计图中”第5组”所在扇形圆心角的度数;
(3)若该校共有1800名学生,那么成绩高于80分的共有多少人?
【思路分析】(1)根据图表中的对应数据求出总人数,进而求出第2组和第4组的人数;(2)根据总人数和第5组人数求出百分比,进而求出圆心角度数;(3)根据总人数和80分以上人数求出百分比,进而求出全校成绩高于80分的学生人数.
【解题过程】(1)由统计图表中可知:第3组人数为10人,占比25%,∴总人数=10÷25%=40(人),第2组占比为30%,∴第2组的人数为40×30%=12(人),故a=12;第4组人数为40-8-12-10-3=7(人),故b=7;
(2)第5组人数为3人,∴圆心角为:360°×=27°,∴”第5组”所在扇形圆心角的度数为27°;
(3)这40名同学中,成绩高于80分的有8+12=20(人),所占百分比为:=50%,1800×50%=900(人),∴全校成绩高于80分的学生共有900人.
【知识点】统计表,扇形统计图,求圆心角,样本估计总体.
6.(2019江苏无锡,23,8分)《国家学生体质健康标准》规定:体质测试成绩达到90.0分及以上的为优秀;达到80.0分至89.9分的为良好;达到60.0分至79.9分的为及格;59.9分及以下为不及格,某校为了了解九年级学生体质健康状况,从该校九年级学生中随机抽取了10%的学生进行体质测试,测试结果如下面的统计表和扇形统计图所示.
各等级学生平均分统计表各等级学生人数分布扇形统计图
等级
优秀
良好
及格
不及格
平均分
92.1
85.0
69.2
41.3
(1) 扇形统计图中“不及格”所占的百分比是 ;
(2) 计算所抽取的学生的测试成绩的平均分;
(3) 若所抽取的学生中所有不及格等级学生的总分恰好等于某一个良好等级学生的分数,请估计该九年级学生中约有多少人达到优秀等级.
【思路分析】本题考查的是表格和扇形统计图的综合运用.
(1)根据扇形统计图的定义,各部分占总体的百分比之和为1,由扇形图可知,不及格人数所占的百分比是1-52%-26%-18%=4%;
(2)抽取的学生平均得分=各等级学生的平均分数×所占百分比的和;
(3)设总人数为n个,列不等式组求n的范围,再求整数解,最后九年级学生的优秀人数.
【解题过程】(1)1-52%-26%-18%= 4%;
(2)92.1×52%+85.0×26%+69.2×18%+41.3×4%=84.1;
(3)设总人数为n个,80.0 ≤ 41.3×n×4%≤89.9,所以 48
7.(2019甘肃天水,20,8分)天水市某中学为了解学校艺术社团活动的开展情况,在全校范围内随机抽取了部分学生,在“舞蹈、乐器、声乐、戏曲、其它活动”项目中,围绕你最喜欢哪一项活动(每人只限一项)进行了问卷调查,并将调查结果绘制成如下两幅不完整的统计图.
请你根据统计图解答下列问题:
(1)在这次调查中,一共抽查了 名学生.
(2)请你补全条形统计图.
(3)扇形统计图中喜欢“乐器”部分扇形的圆心角为 度.
(4)请根据样本数据,估计该校1200名学生中喜欢“舞蹈”项目的共多少名学生?
【思路分析】(1)用喜欢声乐的人数除以它所占的百分比得到调查的总人数;
(2)先计算出喜欢戏曲的人数,然后补全条形统计图;
(3)用360度乘以喜欢乐器的人数所占得到百分比得到扇形统计图中喜欢“乐器”部分扇形的圆心角的度数;
(4)用1200乘以样本中喜欢舞蹈的人数所占的百分比即可.
【解题过程】解:(1)8÷16%=50,
所以在这次调查中,一共抽查了50名学生;
(2)喜欢戏曲的人数为50﹣8﹣10﹣12﹣16=4(人),
条形统计图为:
(3)扇形统计图中喜欢“乐器”部分扇形的圆心角的度数为360°115.2°;
故答案为50;115.2;
(4)1200288,
所以估计该校1200名学生中喜欢“舞蹈”项目的共288名学生.
【知识点】用样本估计总体;扇形统计图;条形统计图
8.(2019贵州黔东南,23,14分)某地区在所有中学开展《老师,我想对你说》心灵信箱活动,为师生之间的沟通增设了一个书面交流的渠道.为了解两年来活动开展的情况,某课题组从全地区随机抽取部分中学生进行问卷调查.对“两年来,你通过心灵信箱给老师总共投递过封信?”这一调查项设有四个回答选项,选项A:没有投过;选项B:一封;选项C:两;选项D:三封及以上.根据接受问卷调查学生的回答,统计出各选项的人数以及所占百分比,分别绘制成如下条形统计图和扇形统计图:
(1)此次抽样调查了 名学生,条形统计图中m= ,n= ;
(2)请将条形统计图补全;
(3)接受问卷调查的学生在活动中投出的信件总数至少有 封;
(4)全地区中学生共有110000名,由此次调查估算,在此项活动中,全地区给老师投过信件的学生约有多少名?
【思路分析】(1)由B选项人数及其所占百分比求得总人数,再用总人数乘以对应百分比可得m、n的值;
(2)先求出C选项的人数,继而可补全图形;
(3)各选项次数乘以对应人数,再求和即可得;
(4)利用样本估计总体思想求解可得.
【解题过程】解:(1)此次调查的总人数为150÷30%=500(人),
则m=500×45%=225,n=500×5%=25,
故答案为:500,225,25;
(2)C选项人数为500×20%=100(人),
补全图形如下:
(3)1×150+2×100+3×25=425,
答:接受问卷调查的学生在活动中投出的信件总数至少有425封,
故答案为:425;
(4)由此次调查估算,在此项活动中,全地区给老师投过信件的学生约有110000×(1﹣45%)=60500(名).
【知识点】全面调查与抽样调查;用样本估计总体;扇形统计图;条形统计图
2023年中考数学 章节专项练习43 概率: 这是一份2023年中考数学 章节专项练习43 概率,共8页。
2023年中考数学 章节专项练习42 数据的分析: 这是一份2023年中考数学 章节专项练习42 数据的分析,共18页。试卷主要包含了2D,5 2等内容,欢迎下载使用。
2023年中考数学 章节专项练习35 与圆的有关计算: 这是一份2023年中考数学 章节专项练习35 与圆的有关计算,共16页。












