2023.4海淀区初三一模数学答案

这是一份2023.4海淀区初三一模数学答案，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
海淀区九年级第二学期期中练习数学试卷答案第一部分　选择题一、选择题 （共16分，每题2分）题号12345678答案ABADBCCC第二部分　非选择题二、填空题（共16分，每题2分）9．      10．     11． 12．16.4                  13．                    14．() 15．35（答案不唯一）        16．2，135三、解答题（共68分，第17-20题，每题5分，第21题6分，第22题5分，第23-24题，每题6分，第25题5分，第26题6分，第27-28题，每题7分）
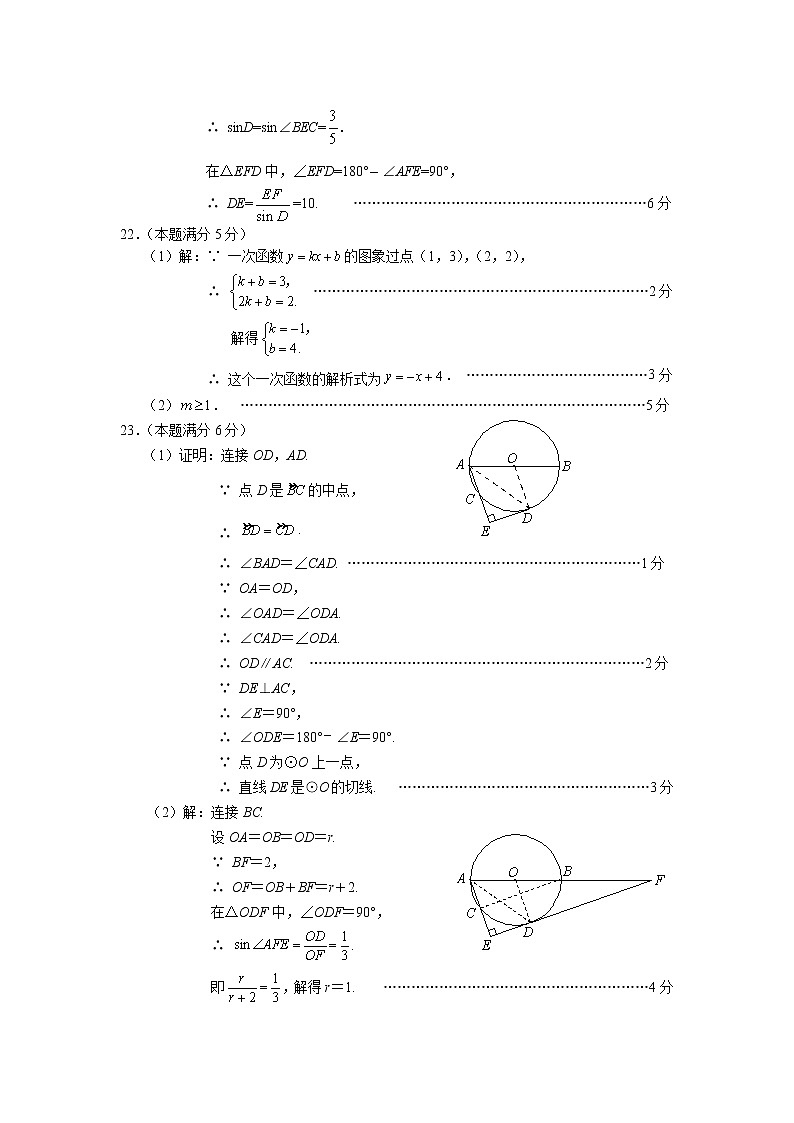
解答应写出文字说明、演算步骤或证明过程．17．（本题满分5分）解：原式   ………………………………………………………………4分． ………………………………………………………………………5分18．（本题满分5分）解：原不等式组为解不等式①，得．   …………………………………………………………2分解不等式②，得．   …………………………………………………………4分∴ 原不等式组的解集为．    ……………………………………………5分19．（本题满分5分） 解：原式=     ……………………………………………………2分            =．   ………………………………………………………………3分∵ ，∴ ．   …………………………………………………………………4分∴ 原式 ==9．   ……………………………………………………………………5分   20．（本题满分5分）方法一证明：在△ABC中，∠ACB＝90°，∴ AC⊥BD．∵ CD＝BC，∴ AB=AD．……………………………………2分∵ ∠BAC＝30°，∴ ∠B＝90°∠BAC＝60°．………………3分∴ △ABD是等边三角形．…………………4分∴ AB＝BD．∴ ．…………………………………………………………5分方法二证明：在△ABC中，∠ACB＝90°，∠BAC＝30°，∴ ∠B＝90°∠BAC＝60°. …………………1分∵ BD＝BC，∴ △BCD是等边三角形. ……………………2分∴ ∠BDC＝60°，BD＝CD.∴ ∠DCA＝∠BDC∠A＝30°＝∠A.∴ CD＝AD. ………………………………………………………………………4分∴ AD＝BD＝BC.∴ .  …………………………………………………………………5分21. （本题满分6分）（1）证明：∵ BE∥AD且AF=BE，∴ 四边形ABEF为平行四边形.  …………………………………………2分∵ ∠A=90°，∴ 四边形ABEF为矩形.  …………………………………………………3分（2）解：∵ 四边形ABEF为矩形，AB=6，∴ ∠AFE=90°，EF=AB=6.在△BCE中，∠C=90°，BC=3，CE=4，∴ BE==5.    …………………………………………………4分∴ sin∠BEC==.∵ BE∥AD，∴ ∠BEC=∠D.∴ sinD=sin∠BEC=.在△EFD中，∠EFD=180°∠AFE=90°，∴ DE==10.     ………………………………………………………6分22．（本题满分5分）（1）解：∵ 一次函数的图象过点（1，3），（2，2），∴   ………………………………………………………………2分解得 ∴ 这个一次函数的解析式为． …………………………………3分（2）．  ……………………………………………………………………………5分23．（本题满分6分）（1）证明：连接OD，AD.∵ 点D是的中点，∴ .∴ ∠BAD＝∠CAD. ………………………………………………………1分∵ OA＝OD，∴ ∠OAD＝∠ODA. ∴ ∠CAD＝∠ODA.∴ OD∥AC.  ………………………………………………………………2分∵ DE⊥AC，∴ ∠E＝90°，∴ ∠ODE＝180°∠E＝90°.∵ 点D为⊙O上一点，∴ 直线DE是⊙O的切线.   ………………………………………………3分（2）解：连接BC.设OA＝OB＝OD＝r.∵ BF＝2，∴ OF＝OB＋BF＝r＋2.在△ODF中，∠ODF＝90°，∴ .即，解得r＝1.    …………………………………………………4分∴ AB＝2r＝2.∵ AB是⊙O的直径，∴ ∠ACB＝90°＝∠E.∴ BC∥EF.∴ ∠ABC＝∠AFE.∴ .∴ .  ………………………………………………6分24．（本题满分6分）（1）6.5，6；  ……………………………………………………………………………2分（2）西红柿；  ……………………………………………………………………………4分（3）6．  ……………………………………………………………………………………6分25．（本题满分5分）（1）① 2.8，0.98； ………………………………………………………………………2分② 由题意可知，抛物线的顶点为（1.4，0.98）.∴ 设抛物线解析式为.   ………………………………3分∵ 当x＝0时，y＝0，∴ ，解得 .∴ 抛物线的解析式为.   ……………………………4分（2）能. ……………………………………………………………………………………5分26.（本题满分6分）（1）m=n.  …………………………………………………………………………………1分理由如下：∵ b=5，∴ 抛物线解析式为y=x210x+1，∴ 对称轴为x=5.∵ x0=3，∴ A（3，m），B（7，n）关于直线x=5对称.∴ m=n. ………………………………………………………………………………2分（2）当时，∵ ，在抛物线上，∴ ，.∵ ，∴ .∴ .当时，∵ ，在抛物线上，∴ ，.∵ ，∴ .∴ .∵ 对于，都有，∴ .当时，设点关于抛物线的对称轴的对称点为，∵ 点在抛物线上，∴ 点在抛物线上.由，得.∵ ，，∴ .∵ 抛物线，∴ 抛物线与y轴交于（0，1）.当时，y随x的增大而减小.∵ 点（0，1），，在抛物线上，且，∴ .综上所述，. ………………………………………………………………6分27.（本题满分7分）（1）∵ 四边形ABCD是正方形，       ∴ AB=BC，∠ABE=∠BCF=90°.       又∵ BE=CF，       ∴ △ABE≌△BCF（SAS）. ………………………………………………………1分       ∴ ∠BAE=∠FBC.       ∵ ∠FBC+∠ABG=90°，       ∴ ∠BAE+∠ABG=90°.       ∴ ∠AGF=90°.   …………………………………………………………………2分（2）① 依题意补全图形.  …………………………………………………………………………………3分② 线段MN与ND的数量关系为MN=ND.   …………………………………4分证明：过点A作AH⊥AE交GN延长线于点H，连接DH.       ∵ ∠AGF=90°，GN平分∠AGF，       ∴ ∠AGN=∠AGF=45°.       ∵ AH⊥AE，       ∴ ∠GAH=90°.       ∴ ∠AHG=∠AGH=45°.       ∴ AG=AH.       ∵ 四边形ABCD是正方形，       ∴ ∠BAD=90°，AB=AD.∵ ∠GAH=90°，       ∴ ∠BAG=∠DAH.       ∴ △BAG≌△DAH（SAS）.       ∴ BG=DH，∠AHD=∠AGB=90°.       ∵ BG=GM，∠AHG=45°，       ∴ GM=DH，∠DHN=∠NGM=45°.∵ ∠HND=∠GNM，       ∴ △HND≌△GNM（AAS）.       ∴ MN=ND.   ……………………………………………………………7分28.（本题满分7分）（1）① y=x+2；……………………………………………………………………………1分② ；   ……………………………………………………………………………2分（2）① 当d=2时，直线CD过点（0，2），（2，0），∴ 直线CD解析式为y=x+2.∵ 点M在直线CD上，∴ 设M点坐标为（m，m+2）.∴ 点M的关联直线为l：y=mxm+2.∴ 直线l过定点H（1，2），则.∵ 点O到直线l的距离，∴ ，当OH⊥l，即时，.∴ 点O到点M的关联直线的距离的最大值为.  …………………………5分② d=2或d=.  …………………………………………………………………7分