专题06 《边边边判定三角形全等》重难点题型分类（原卷版+解析版）-【黑马逆袭必刷题】2022-2023学年八年级数学上册拔尖题精选精练（苏科版）

这是一份专题06 《边边边判定三角形全等》重难点题型分类（原卷版+解析版）-【黑马逆袭必刷题】2022-2023学年八年级数学上册拔尖题精选精练（苏科版），文件包含专题06《边边边判定三角形全等》重难点题型分类解析版docx、专题06《边边边判定三角形全等》重难点题型分类原卷版docx等2份试卷配套教学资源，其中试卷共39页， 欢迎下载使用。
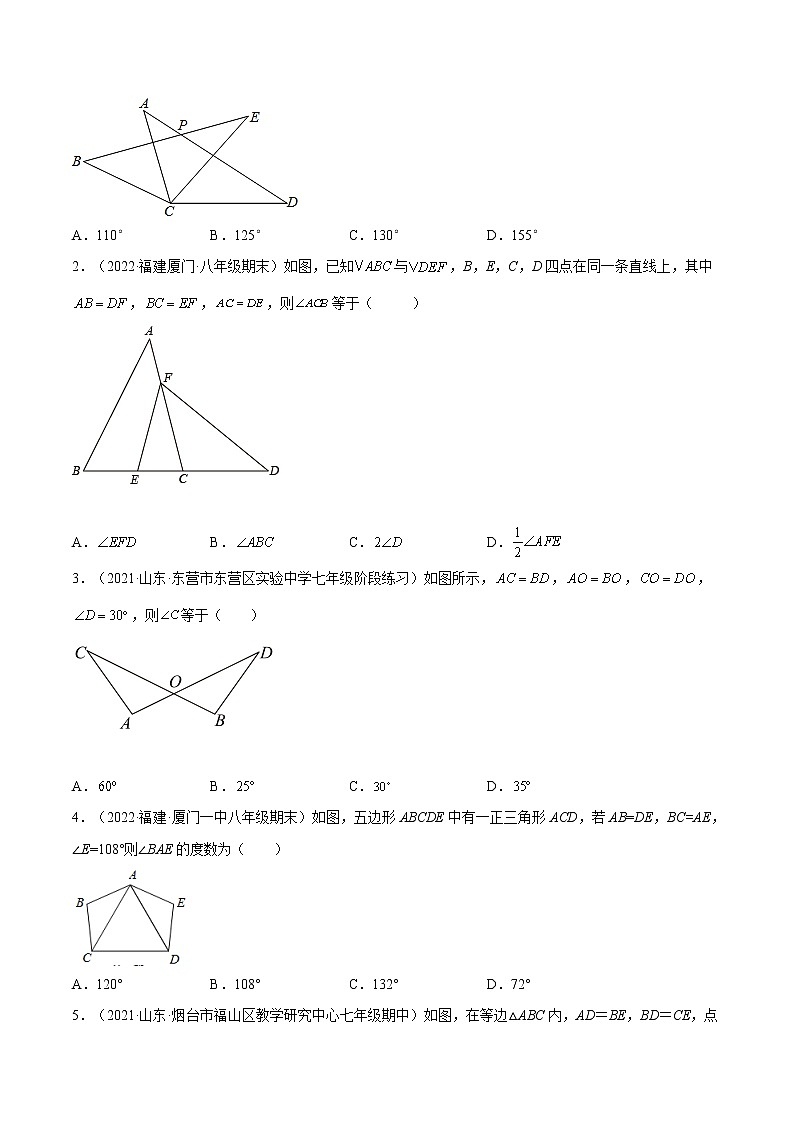
专题06 《边边边判定三角形全等》重难点题型分类专题简介：本份资料专攻《边边边判定三角形全等》中“边边边判定三角形全等的条件”、“边边边求角的度数”、“边边边求线段的长度”、“边边边判定三角形全等的证明题”、“边边边判定三角形全等的探究题”等重点题型；适用于老师给学生作复习培训时使用或者考前刷题时使用。考点1：边边边判定三角形全等的条件方法点拨：三边对应相等的两个三角形全等，简写为“边边边”或“SSS”。1．（2022·辽宁·锦州市太和区教师进修学校七年级期中）如图，在平分角的仪器中，AB＝AD，BC＝DC，将点A放在一个角的顶点，AB和AD分别与这个角的两边重合，能说明AC就是这个角的平分线的数学依据是（　　） A．SSS B．ASA C．SAS D．AAS2．（2022·吉林白山·二模）仔细观察用直尺和圆规作一个角等于已知角的示意图，请根据三角形全等的有关知识，说明画出的依据是（       ）A． B． C． D．3．（2022·河南南阳·二模）作一个三角形与已知三角形全等：已知：．求作：，使得．作法：如图．（1）画；（2）分别以点，为圆心，线段AB，AC长为半径画弧，两弧相交于点；（3）连接线段，，则即为所求作的三角形． 这种作一个三角形与已知三角形全等的方法的依据是（       ）A．AAS B．ASA C．SAS D．SSS4．（2022·全国·八年级）如图，已知，根据“SSS”，还需要一个条件________，可证明．5．（2022·江苏镇江·一模）已知中，，以点B为圆心，AB长为半径画弧，再以点C圆心，AC长为半径画弧，两弧相交于点D，你有哪些发现？写出一个即可：________．考点2：边边边求角的度数方法点拨：利用全等三角形性质求线段的长度和角的度数，是利用全等三角形性质的一种考法。在求解时直接运用全等三角形的性质，得到对应边（或对应角）间的相等关系，再进行等量替换及和差运算，求线段的长度或角的度数。这类题目的答题思路是：由两个三角形全等找出对应角及对应边，再利用已知条件，结合对顶角、三角形内角和等的性质求解。1．（2022·全国·八年级）平面上有△ACD与△BCE，其中AD与BE相交于P点，如图．若AC＝BC，AD＝BE，CD＝CE，∠ACE＝55°，∠BCD＝155°，则∠BPD的度数为（　　）A．110° B．125° C．130° D．155°2．（2022·福建厦门·八年级期末）如图，已知与，B，E，C，D四点在同一条直线上，其中，，，则等于（       ） A． B． C． D．3．（2021·山东·东营市东营区实验中学七年级阶段练习）如图所示，，，，，则等于（     ） A． B． C． D．4．（2022·福建·厦门一中八年级期末）如图，五边形ABCDE中有一正三角形ACD，若AB=DE，BC=AE，∠E=108°则∠BAE的度数为（　　）A．120° B．108° C．132° D．72°5．（2021·山东·烟台市福山区教学研究中心七年级期中）如图，在等边△ABC内，AD＝BE，BD＝CE，点D在BE上，若∠CBE＝15°，则∠CAD的度数为__________．6．（2022·河南新乡·八年级期末）如图，在△ABC中，∠ACB=90°，AC=BC，点E为△ABC内一点，AE=BE．延长AE至点D，使DE=AC，连接CD，CE．若CD=DE，则∠D的度数是____________．7．（2021·上海·青浦区实验中学七年级期末）如图，点B、C、E三点在同一直线上，且AB＝AD，AC＝AE，BC＝DE，若，则∠3＝______°．考点3：边边边求线段的长度方法点拨：利用全等三角形性质求线段的长度，是利用全等三角形性质的一种考法。在求解时直接运用全等三角形的性质，得到对应边间的相等关系，再进行等量替换及和差运算，求线段的长度。1．（2022·福建三明·七年级期末）如图所示，等腰中，，将沿对折，顶点落在边点处，若，，那么的长度是_____________2．（2022·广西·中考真题）校园内有一块四边形的草坪造型，课外活动小组实地测量，并记录数据，根据造型画如图的四边形ABCD，其中 AB＝CD＝2米，AD＝BC＝3米，∠B＝(1)求证：△ABC≌△CDA ；(2)求草坪造型的面积．3．（2022·全国·八年级阶段练习）如图，在△ABC与△ABD中，AC = BD，且CE = DE，AE = BE，AD与BC交于点E．（1）求证：△ACE ≌ △BDE；（2）若AC = 3，BC = 5，求△ACE的周长．4．（2022·云南·昆明市官渡区第一中学八年级期中）如图，点在同一条直线上，．（1）求证：；（2）若AD=3，DC=5，求DF的长度．5．（2022·浙江绍兴·八年级期末）已知：如图，AB＝AD，BC＝DC，E、F分别是DC、BC的中点   （1）求证： ∠D=∠B；（2）当AE=2时，求AF的值．考点4：边边边判定三角形全等的证明题方法点拨：利用“SSS”判定两个三角形全等时，必须满足“三边对应相等”这一条件。1．（2022·陕西·西安工业大学附中三模）如图，在中，点E，F分别在，上，且，． 求证：．2．（2021·福建泉州·八年级期末）如图，在和中，，，和分别是边和上的中线，且．求证：．3．（2022·广西贺州·八年级期末）已知：如图，点A，D，C，B在同一条直线上，AD=BC，AE=BF，CE=DF，求证： (1)△AEC≌△BFD(2)DE=CF4．（2022·辽宁盘锦·八年级期末）如图，点C在线段AB上，CF为线段DE的垂直平分线，AC= EB，AD=BC试探究AD与EB的位置关系，并说明理由．5．（2022·广东·深圳大学附属中学七年级期中）如图，点A、B、C、D在同一直线上，AM=CN，BM=DN，AC=BD．求证：BM//DN.6．（2022·全国·八年级）如图，AD＝CB，E，F是AC上两动点，且有DE＝BF(1)若E，F运动如图①所示的位置，且有AF＝CE，求证：△ADE≌△CBF；(2)若E，F运动如图②所示的位置，仍有AF＝CE，那么△ADE≌△CBF还成立吗？为什么？(3)若E，F不重合，AD和CB平行吗？说明理由．考点5：边边边判定三角形全等的探究题方法点拨：边边边——三边对应相等的两个三角形全等。1．（2022·河北沧州·八年级期中）定义：两组邻边分别相等的四边形称为筝形．如图，在四边形ABCD中，AB=AD，BC=DC，AC与BD相交于点O，四边形ABCD即为筝形．下列判断：①AC⊥BD ②AC、BD互相平分 ③AC平分∠BCD ④∠ABC=∠ADC=90°⑤筝形ABCD的面积为AC•BD．正确的有（       ）A．①③④ B．①③⑤ C．①④⑤ D．③④⑤2．（2021·湖北·安陆市陈店乡初级中学八年级阶段练习）如图，在四边形ABCD中，AD＝BC＝8，AB＝CD，BD＝12，点E从D点出发，以每秒1个单位的速度沿DA向点A匀速移动，点F从点C出发，以每秒3个单位的速度沿C→B→C，作匀速移动，点G从点B出发沿BD向点D匀速移动，三个点同时出发，当有一个点到达终点时，其余两点也随之停止运动，假设移动时间为t秒．（1）试证明：AD∥BC；（2）在移动过程中，小明发现有与全等的情况出现，请你探究这样的情况会出现几次？并分别求出此时的移动时间和G点的移动距离．3．（2021·全国·八年级期末）阅读材料：课本中研究图形的性质，就是探究图形的构成元素（边、角、有关线段）具有怎样的特征．例如在学习等腰三角形的性质时，我们就探究得出了等腰三角形有如下性质：边的性质：等腰三角形两腰相等；角的性质：等腰三角形的两个底角相等；有关线段的性质：等腰三角形顶角的平分线、底边上的高、底边的中线是同一条线段．如果两组邻边分别相等的四边形叫筝形．如图，在四边形，若， ，则四边形是筝形．请探究筝形的性质，写出两条并进行证明（边的性质除外）．4．（2022·广西玉林·中考真题）问题情境：在数学探究活动中，老师给出了如图的图形及下面三个等式：①        ②        ③若以其中两个等式作为已知条件，能否得到余下一个等式成立？解决方案：探究与全等．问题解决：(1)当选择①②作为已知条件时，与全等吗？_____________（填“全等”或“不全等”），理由是_____________；(2)当任意选择两个等式作为已知条件时，请用画树状图法或列表法求的概率．5．（2022·山西吕梁·八年级期中）下面是关于探究勾股定理逆定理的一个片断，请你认真阅读并完成相应任务．如果三角形的三边长，，满足，那么这个三角形是直角三角形．已知：如图1，的三边长分别是，，，且满足．求证：是直角三角形． 分析：要证明是直角三角形，可以先作一个，使，，如果与全等，那么就是直角三角形．(1)任务一：请在上述虚线方框内按材料中“分析”的思路画出；（要求：尺规作图，不写作法，保留作图痕迹）(2)任务二：请你按材料“分析”的思路证明是直角三角形；(3)任务三：如图2，正方形的边长为4，点是边的中点，．求证：．