2023届四川大学附属中学（四川省成都市第十二中学）高三下学期二诊热身考试数学（文）试题含解析

2023届四川大学附属中学（四川省成都市第十二中学）高三下学期二诊热身考试数学（文）试题

一、单选题

1．已知复数满足，为虚数单位，则（    ）

A． B． C． D．

【答案】B

【分析】根据向量的除法和向量模的求法，变形的，即可求解.

【详解】，

故选：B

2．设集合或，，则集合（    ）

A． B． C． D．

【答案】B

【分析】利用对数函数性质化简集合，再结合交集的运算求解即可.

【详解】由题知，，

又或，

则，即.

故选：B

3．抛物线的准线方程是（    ）

A． B．

C． D．

【答案】A

【分析】先化为标准型，利用抛物线的准线方程可得答案.

【详解】因为，所以，所以准线方程为.

故选：A.

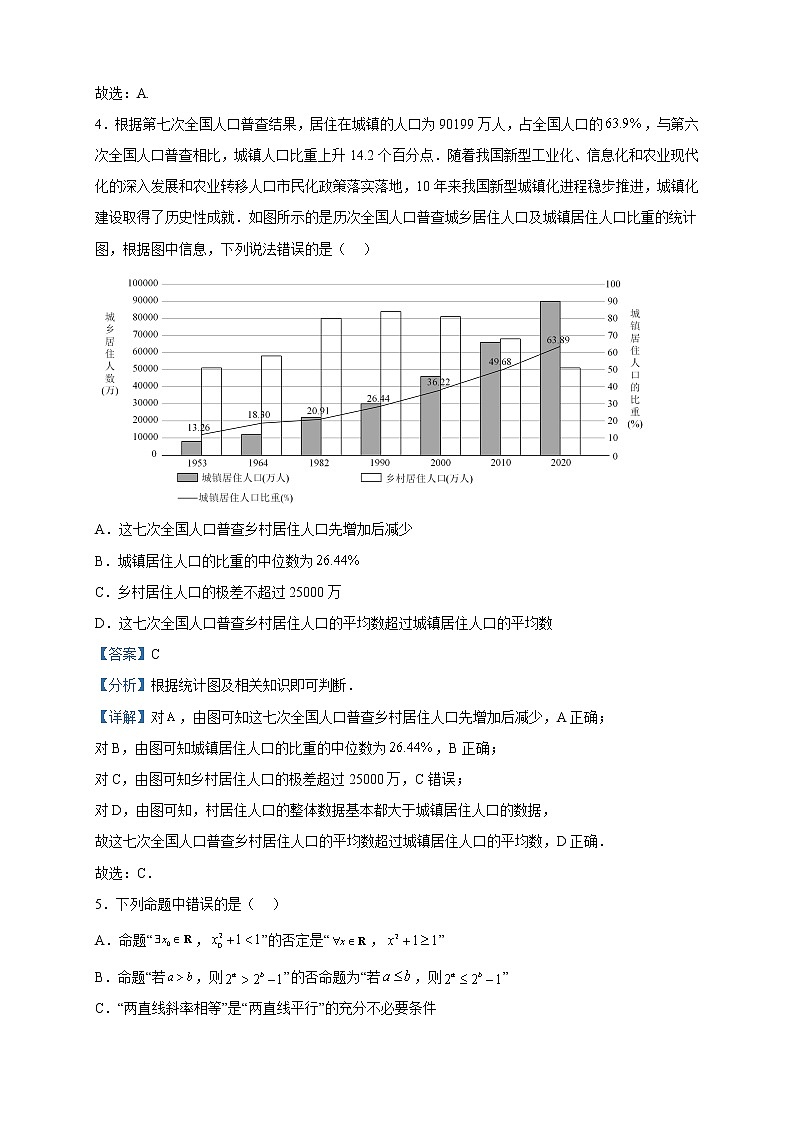
4．根据第七次全国人口普查结果，居住在城镇的人口为90199万人，占全国人口的，与第六次全国人口普查相比，城镇人口比重上升14.2个百分点．随着我国新型工业化、信息化和农业现代化的深入发展和农业转移人口市民化政策落实落地，10年来我国新型城镇化进程稳步推进，城镇化建设取得了历史性成就．如图所示的是历次全国人口普查城乡居住人口及城镇居住人口比重的统计图，根据图中信息，下列说法错误的是（    ）

A．这七次全国人口普查乡村居住人口先增加后减少

B．城镇居住人口的比重的中位数为

C．乡村居住人口的极差不超过25000万

D．这七次全国人口普查乡村居住人口的平均数超过城镇居住人口的平均数

【答案】C

【分析】根据统计图及相关知识即可判断．

【详解】对，由图可知这七次全国人口普查乡村居住人口先增加后减少，A正确；

对B，由图可知城镇居住人口的比重的中位数为，B正确；

对C，由图可知乡村居住人口的极差超过25000万，C错误；

对D，由图可知，村居住人口的整体数据基本都大于城镇居住人口的数据，

故这七次全国人口普查乡村居住人口的平均数超过城镇居住人口的平均数，D正确．

故选：C．

5．下列命题中错误的是（    ）

A．命题“，”的否定是“，”

B．命题“若，则”的否命题为“若，则”

C．“两直线斜率相等”是“两直线平行”的充分不必要条件

D．若“p或q”为假命题，则p，q均为假命题

【答案】C

【分析】根据存在量词命题的否定为全称量词命题即可判断A；根据否命题的定义即可判断B；根据两直线的斜率与平行的关系即可判断C；根据复合命题的真假即可判断D.

【详解】对于A，命题“，”的否定是“，”，故A正确；

对于B，命题“若，则”的否命题为“若，则”，故B正确；

对于C，若两直线斜率相等，则两直线平行或重合，

若两直线平行，则两直线斜率相等，或两直线斜率都不存在，

所以“两直线斜率相等”是“两直线平行”的既不充分也不必要条件，故C错误；

对于D，若“p或q”为假命题，则p，q均为假命题，故D正确.

故选：C.

6．已知，，执行如图所示的程序框图，输出的值为（    ）

A．2 B． C． D．1

【答案】B

【分析】根据程序框图比较的大小，输出三个数中的最小值.

【详解】根据程序框图可知，执行程序输出的结果是三个数中的最小值.

因为，，，

所以，所以输出的值为.

故选：B.

7．若点是曲线上任意一点，则点到直线距离的最小值为（    ）

A． B． C． D．

【答案】C

【分析】由题知过点作曲线的切线，当切线与直线平行时，点到直线距离的最小，再根据导数的几何意义求解即可.

【详解】解：过点作曲线的切线，当切线与直线平行时，点到直线距离的最小.

设切点为，，

所以，切线斜率为，

由题知得或（舍），

所以，，此时点到直线距离.

故选：C

8．如图，在平面四边形中，，，，，三角形的面积为，则（    ）

A．2 B．4 C． D．

【答案】B

【分析】由正弦定理，结合，，可得.由三角形的面积为，可得.由余弦定理可得，后可得答案.

【详解】在中，，

由正弦定理有：，即，解得.

由三角形的面积公式有：，则.

在中，由余弦定理有：.

则.

故选：B

9．如图，一个棱长1分米的正方体形封闭容器中盛有V升的水，若将该容器任意放置均不能使水平面呈三角形，则V的取值范围是（    ）

A． B． C． D．

【答案】A

【分析】找到水最多和水最少的临界情况，如图分别为多面体和三棱锥，从而可得出答案.

【详解】将该容器任意放置均不能使水平面呈三角形，

则如图，水最少的临界情况为，水面为面，

水最多的临界情况为多面体，水面为，

因为，

，

所以，即.

故选：A.

10．已知函数的图象如图所示，图象与轴的交点为，与轴的交点为，最高点，且满足．若将的图象向左平移1个单位得到的图象对应的函数为，则（    ）

A． B．0 C． D．

【答案】D

【分析】根据题意得，，进而得，再根据结合向量垂直关系的表示解得，进而得，再根据平移变换得，最后求函数值即可.

【详解】解：由题知，函数的周期满足，解得，

所以，

由图象与轴的交点为得，

因为，所以，即，

所以，图象与轴的交点为，

因为，所以，解得（负舍），

所以，

所以若将的图象向左平移1个单位得到的图象对应的函数为 ，

所以.

故选：D

11．已知圆锥的侧面展图为一个半圆，则该圆锥内半径最大的球的表面积与圆锥外接球的表面积之比为（    ）

A． B． C． D．

【答案】C

【分析】根据圆锥的侧面展图为一个半圆得出圆锥母线长与半径的关系，再利用圆锥内半径最大的球即圆锥的内切球，然后分别求出圆锥的内切球和圆锥外接球的半径即可求解.

【详解】由题意可知，设圆锥的母线长为，半径为，则

因为圆锥的侧面展图为一个半圆，所以，解得.

圆锥内半径最大的球即圆锥的内切球，设内切球半径为，设圆锥的一个轴截面为，如图所示

则内切圆的半径为圆锥内切球的半径，在中，，为的中点，，

所以为等边三角形，则,即，解得，

所以圆锥内半径最大的球的表面积为.

又外接圆的直径为，

所以圆锥的外接球的半径，

所以圆锥外接球的表面积为

所以.

故选：C.

12．已知函数有三个零点，且，则（    ）

A．8 B．1 C．－8 D．－27

【答案】D

【分析】根据题意可得：有三解，令，由的图像可得故最多只有两个解，所以有两解，，有一解为，有两解为，代入即可得解.

【详解】由，

即有三解，

令，设，

，

当，为增函数，

当，为减函数，

图像如图所示：

故最多只有两个解，

若要有三解，

则有两解，

，，

故有一解为，

有两解为，

，

故选：D

二、填空题

13．若x，y满足，则的最大值为______．

【答案】

【分析】由的几何意义得出的最大值.

【详解】该不等式组表示的平面区域如下图所示：

可变形为，平移直线，当该直线过点时，

取最大值，最大值为.

故答案为：

14．下表提供了某学生做题数量x（道）与做题时间y（分钟）的几组对应数据：

根据上表提供的数据，得y关于x的线性回归方程为则表中t的值为_____．

【答案】3

【分析】现求出样本的中心点，再代入回归直线的方程，即可求得的值.

【详解】由题意可得，

因为对的回归直线方程是，

所以，解得.

【点睛】本题主要考查了回归直线方程的应用，其中解答的关键是利用回归直线方程恒过样本中心点，代入求解，着重考查了推理与计算能力，属于基础题.

15．如图，若坐标轴和双曲线与圆的交点将圆的周长八等分，且，则该双曲线的渐近线方程为______．

【答案】

【分析】根据圆的性质，结合代入法、双曲线渐近线方程进行求解即可.

【详解】

设双曲线的标准方程为，

设圆与双曲线在第一象限内的交点为，连接、，

则，

因为坐标轴和双曲线与圆的交点将圆的周长八等分，则，

故点，

将点的坐标代入双曲线的方程可得，所以，

所以该双曲线的渐近线方程为．

故答案为：

16．如图，在扇形中，，，点为的中点，点为曲边区域内任一点（含边界），若，则的最大值为________．

【答案】

【分析】建立直角坐标系，根据向量的坐标运算即可得，，进而根据线性规划求截距最大或者根据三角换元法即可求解.

【详解】建立平面直角坐标系如图所示，

设，则，；

，；

由是区间内的任意点，且，

，，，

，；，，

，设，即，

用线性区域的方法，平移直到于圆弧相切，与轴相交于,

此时直线截距最大，切点就是满足条件的点；

由于此时切线的斜率为

此时,由此，

故,因此此时，

即的最大值为，

故答案为：.

三、解答题

17．已知数列的前n项和为，，且．，．

(1)求数列和的通项公式；

(2)若，求数列的前n项和．

【答案】(1)，

(2)

【分析】（1）根据对数运算得，利用等比数列定义求通项公式，利用等差中项判断数列为等差数列，建立方程求出公差，从而可得的通项；

（2）利用错位相减法计算即可.

【详解】（1）∵，∴，则，所以为等比数列，

又，得，所以，

由知是等差数列，且，，

∴，得，．∴.

（2）因为，，所以，

所以

则

上面两式作差得

，

∴

18．2022年12月2日晚，神舟十四号、神舟十五号航天员乘组进行在轨交接仪式，两个乘组移交了中国空间站的钥匙，6名航天员分别在确认书上签字，中国空间站正式开启长期有人驻留模式．为调查大学生对中国航天事业的了解情况，某大学进行了一次抽样调查，若被调查的男女生人数均为，统计得到以下列联表，经计算，有97.5%的把握认为该校学生对中国航天事业的了解与性别有关，但没有99%的把握认为该校学生对中国航天事业的了解与性别有关．

(1)求n的值．

(2)现采用分层抽样的方法在调查结果“了解中国航天事业”的学生中抽取5人，再从这5人中抽取3人进行第二次调查，以便了解学生获得中国航天事业信息的渠道，则至少有2名男生被第二次调查的概率．

附表：

【答案】(1)2

(2)

【分析】（1）根据已知完成列联表，结合公式进行求解即可；

（2）根据分层抽样的比例比，结合概率加法公式进行求解即可.

【详解】（1）由已知，完成列联表，

将数值代入公式可得的观测值：，

所以，解得，因为，所以．

（2）由上可知了解中国航天事业的男生、女生人数分别为、，

所以根据分层抽样的性质可知：5名学生中男生人数为，

女生人数为，

设事件：至少有2名男生被第二次调查，

.

19．如图（1），已知边长为2的菱形ABCD中，沿对角线BD将其翻折，使，设此时AC的中点为O，如图（2）．

(1)求证：点O是点D在平面上的射影；

(2)求点A到平面BCD的距离．

【答案】(1)证明见解析

(2)

【分析】（1）连接DO，BO，利用勾股定理证明，再证明平面，即可得证；

（2）利用等体积法求解即可.

【详解】（1）连接DO，因为，O为AC的中点，所以，

设菱形ABCD的边长为2，

又因为，所以，连接BO，则，

又因为，，所以，所以，

所以，

又，所以，所以，

又，平面，平面，所以平面，

所以点O是点D在平面上的射影；

（2）设点A到平面BCD的距离为h，

由菱形ABCD的边长为2，且，

则的面积为，

则，的面积为，

由（1）知，平面，，

所以，

由得，，所以，

即点A到平面BCD的距离为．

20．椭圆的光学性质：光线从椭圆的一个焦点出发经椭圆反射后通过另一个焦点.现有一椭圆，长轴长为4，从一个焦点F发出的一条光线经椭圆内壁上一点P反射之后恰好与x轴垂直，且.

(1)求椭圆C的标准方程；

(2)点Q为直线上一点，且Q不在x轴上，直线，与椭圆C的另外一个交点分别为M，N，设，的面积分别为，，求的最大值.

【答案】(1)

(2)

【分析】（1）利用长轴长求出a，利用椭圆定义求出，进一步求出，即可得椭圆方程；（2）设直线，联立方程求出M、N的坐标，把面积比转化为坐标比，进一步转化为分式函数求最值问题

【详解】（1）不妨设、是椭圆的左焦点、右焦点，

则轴，又因为，，

所以，即，所以，

所以椭圆C的方程为.

（2）设，，

则：，：

联立，消去x得，解得，

同理，联立，消去x得，解得，

所以

.

令，

则

当且仅当，即，即时，取得最大值.

21．已知.

(1)若，求函数的单调区间和极值；

(2)若对都有成立，求实数a的取值范围.

【答案】(1)单调增区间为和，单调减区间为；极大值为，极小值为

(2)

【分析】（1）直接求导计算即可．

（2）将问题转化为，构造新函数在上单调递增即可，然后参变分离或者分类讨论都可以．

【详解】（1）

令，因为得或，列表如下：

所以的单调增区间为和  单调减区间为

极大值为  ，极小值为

（2）对都有成立可转化化为：

设，则在，

故，在上恒成立

方法一：（含参讨论）

设，

则，，解得.

，，.

①当时，，

故，当时，，递增；

当时，，递减；

此时，，在上单调递增，故，符合条件.

②当时，同①，当时，递增；当时，递减；

∵，，

∴由连续函数零点存在性定理及单调性知，，.

于是，当时，，单调递增；

当时，，单调递减.

∵，，∴，符合条件.

综上，实数的取值范围是.

方法二：（参变分离）

由对称性，不妨设，

则即为.

设，则在上单调递增，

故在上恒成立.

∵，∴在上恒成立

，.

设，，则，.

设，，

则，.

由，，得在，上单调递增；

由，，得在，上单调递减.

故时；

时.

从而，，，

又时，，故，，

，单调递减，，.

于是，.

综上，实数的取值范围是.

【点睛】本题核心是将问题转化为函数在上单调递增，即在上恒成立．

22．在直角坐标系中，曲线的方程为，曲线的方程为以坐标原点为极点，轴的正半轴为极轴建立极坐标系，直线的极坐标方程为

(1)求曲线，的极坐标方程；

(2)若，直线与曲线交于，两点，与曲线的一个交点为点，且，求的值

【答案】(1)，

(2)

【分析】（1）根据曲线的直角坐标与极坐标转化公式，即可求解；

（2）将代入曲线的极坐标方程，得，将代入曲线的极坐标方程，

得到韦达定理，并表示，即可求.

【详解】（1）由，得，

所以曲线的极坐标方程为

由，得，即，

此即曲线的极坐标方程；

（2）将代入（），得

将代入，得，

设对应的参数分别是，则，，

所以

，

解得：

23．设函数．

(1)解不等式；

(2)令的最小值为T，正数满足，证明：．

【答案】(1).

(2)证明见解析.

【分析】（1）分类讨论x的取值，脱掉绝对值符号，解不等式，可得答案；

（2）分类讨论x的取值，求出的最小值为T，将展开，利用基本不等式证明，即可证明结论.

【详解】（1）当时，即，解得，故；

当时， 即，则；

当时，即，解得，故，

综上所述，原不等式的解集为.

（2）若，则；

若，则：

若，则,

所以函数的最小值，故,

又为正数，

则

,

当且仅当,时等号成立,

所以.