初中数学苏科版八年级下册9.5 三角形的中位线同步练习题

这是一份初中数学苏科版八年级下册9.5 三角形的中位线同步练习题，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题
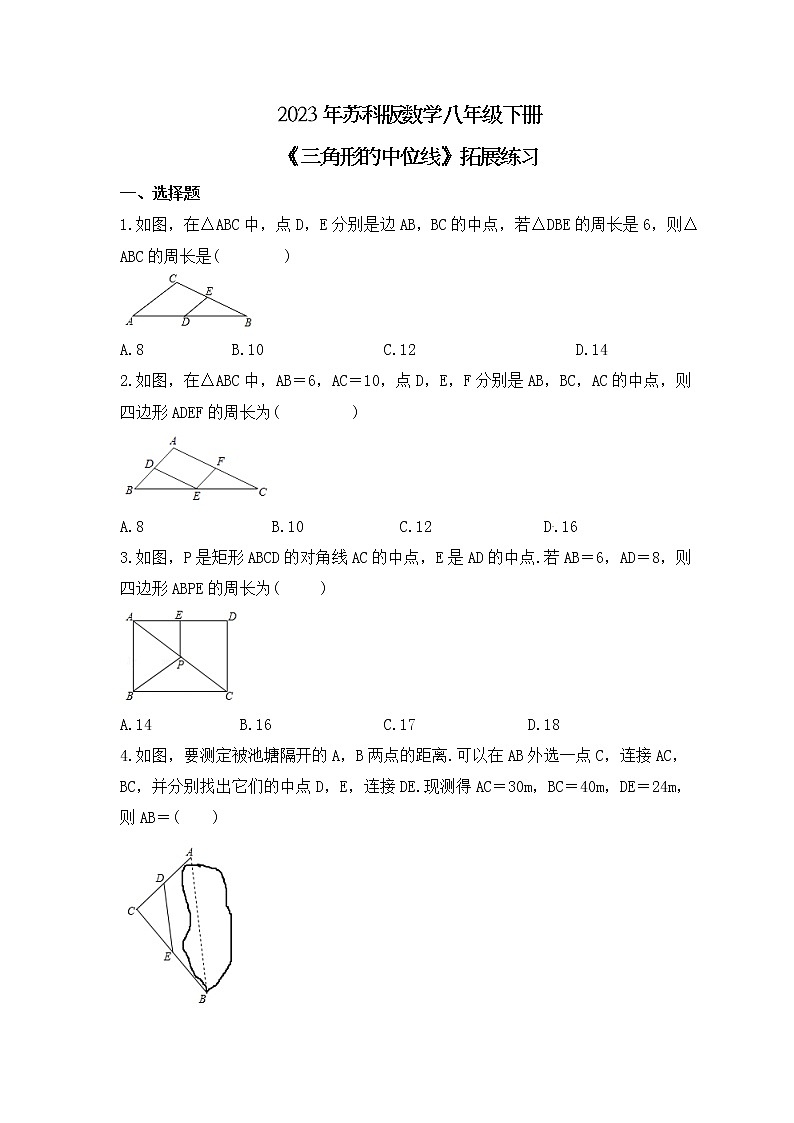
1.如图，在△ABC中，点D，E分别是边AB，BC的中点，若△DBE的周长是6，则△ABC的周长是( )
A.8 B.10 C.12 D.14
2.如图，在△ABC中，AB＝6，AC＝10，点D，E，F分别是AB，BC，AC的中点，则四边形ADEF的周长为( )
A.8 B.10 C.12 D.16
3.如图，P是矩形ABCD的对角线AC的中点，E是AD的中点.若AB＝6，AD＝8，则四边形ABPE的周长为( )
A.14 B.16 C.17 D.18
4.如图，要测定被池塘隔开的A，B两点的距离.可以在AB外选一点C，连接AC，BC，并分别找出它们的中点D，E，连接DE.现测得AC＝30m，BC＝40m，DE＝24m，则AB＝( )
A.50m B.48m C.45m D.35m
5.如图，已知四边形ABCD是平行四边形，对角线AC，BD相交于点O，E是BC的中点，以下说法错误的是( )
A.2OE＝DC B.OA＝OC C.∠BOE＝∠OBA D.∠OBE＝∠OCE
6.如图，平行四边形ABCD中，对角线AC、BD相交于点O，E为CD中点，则△ODE与△ABC的面积比为( )
A.1：2 B.1：3 C.1：4 D.1：5
7.如图，顺次连接四边形ABCD各边中点得四边形EFGH，要使四边形EFGH为矩形，应添加的条件是( )
A.AB∥DC B.AC＝BD C.AC⊥BD D.AB＝DC
8.如图，已知在矩形ABCD中，E、F、G、H分别为边AB、BC、CD、DA的中点.若AB=2，AD=4，则图中阴影部分的面积为( )
A.8 B.6 C.4 D.3
9.依次连接菱形的四边中点得到的四边形一定是( )
A.矩形 B.菱形 C.正方形 D.三角形
10.如图，△ABC的中线BD、CE交于点O，连接OA，点G、F分别为OC、OB的中点，BC=8，AO=6，则四边形DEFG的周长为( )

A.12 B.14 C.16 D.18
11.如图，平行四边形ABCD的对角线AC，BD交于点O，AB＝eq \r(3)，∠AOB＝60°，过点O作OE⊥AC，交AD于点E，过点E作EF⊥BD，垂足为F，则OE＋2EF的值为( )
A.eq \f(\r(3),2)＋1 B.eq \r(3) C.eq \f(\r(7),2) D.eq \f(\r(3),2)＋eq \f(1,2)
12.如图，四边形ABCD中，AB∥CD，AB＝5，DC＝11，AD与BC的和是12，点E、F、G分别是BD、AC、DC的中点，则△EFG的周长是( )
A.8 B.9 C.10 D.12
二、填空题
13.如图，在△ABC中，D，E分别是边AB，AC的中点，若BC＝6，则DE＝ .
14.如图，□ABCD的对角线AC，BD相交于点O，点E、F分别是线段AO、BO的中点，若AC＋BD＝24厘米，△OAB的周长是18厘米，则EF＝ 厘米.
15.如图，A，B两地被池塘隔开，小明通过下面的方法测出 A，B间的距离：先在AB外选一点C，连接AC，BC，分别取AC，BC的中点D，E，测得DE＝15米，由此他知道了A，B间的距离为________米，这种做法的依据是_____________.
16.如图，E，F，G，H分别是矩形ABCD各边中点，AB＝6，BC＝8，则四边形EFGH面积是 ．
17.如图，在△ABC中，M是BC边的中点，AP平分∠A，BP⊥AP于点P，若AB＝12，AC＝22，则MP的长为___________
18.如图，矩形△ABCD中，AB＝2，AD＝1，E为CD中点，P为AB边上一动点(含端点)，F为CP中点，则△CEF的周长最小值为______．
三、解答题
19.如图，在四边形ABCD中，AD∥BC，E是AB的中点，连接DE并延长交CB的延长线于点F，点G在边BC上，且∠GDF＝∠ADF．
(1)求证：△ADE≌△BFE；
(2)连接EG，判断EG与DF的位置关系并说明理由．
20.如图，平行四边形ABCD的对角线AC，BD相交于点O，点E，F分别是线段AO，BO的中点，若AC＋BD＝24，△OAB的周长是18，试求EF的长.
21.如图，在△ABC中，AB＝5，AC＝3，AD，AE分别为△ABC的中线和角平分线，过点C作CH⊥AE于点H，并延长交AB于点F，连接DH，求线段DH的长.
22.如图，△ABC的中线BE，CF相交于点G，P，Q分别是BG，CG的中点．
(1)求证：四边形EFPQ是平行四边形；
(2)请直接写出BG与GE的数量关系： ．(不要求证明)
23.如图，E、F、G、H分别是边AB、BC、CD、DA的中点.当BD、AC满足什么条件时，四边形EFGH是正方形.
24.如图，已知△ABC中，D是BC边的中点，AE平分∠BAC，BE⊥AE于E点，若AB＝5，AC＝7，求ED．
25.已知：如图1，四边形ABCD四条边上的中点分别为E、F、G、H，顺次连接EF、FG、GH、HE，得到四边形EFGH(即四边形ABCD的中点四边形)．
(1)四边形EFGH的形状是 ，证明你的结论．
(2)如图2，请连接四边形ABCD的对角线AC与BD，当AC与BD满足 条件时，四边形EFGH是矩形；证明你的结论．
(3)你学过的哪种特殊四边形的中点四边形是矩形？说明理由．

答案
1.C.
2.D.
3.D
4.B.
5.D.
6.C.
7.C
8.C
9.A.
10.B
11.B.
12.B.
13.答案为：3.
14.答案为：3.
15.答案为：30；三角形中位线性质定理.
16.答案为：24．
17.答案为：5.
18.答案为：eq \r(2)＋1.
19.证明：(1)∵AD∥BC，
∴∠ADE＝∠BFE，
∵E为AB的中点，
∴AE＝BE，
在△AED和△BFE中，
∴△AED≌△BFE(AAS)；
(2)EG与DF的位置关系是EG垂直平分DF，理由为：连接EG，
∵∠GDF＝∠ADE，∠ADE＝∠BFE，
∴∠GDF＝∠BFE，
由(1)△AED≌△BFE得：DE＝EF，
即GE为DF上的中线，
∴GE垂直平分DF．
20.解：∵四边形ABCD是平行四边形
∴AO＝CO，BO＝DO，
∵AC＋BD＝24，
∴AO＋BO＝12，
∵△OAB的周长是18，
∴AB＝18﹣(AO＋BO)＝18﹣12＝6，
∵点E，F分别是线段AO，BO的中点
∴EF＝3.
21.解：∵AE为△ABC的角平分线，
∴∠FAH＝∠CAH.
∵CH⊥AE，
∴∠AHF＝∠AHC＝90°.
在△AHF和△AHC中，
eq \b\lc\{(\a\vs4\al\c1(∠FAH＝∠CAH，,AH＝AH，,∠AHF＝∠AHC，))
∴△AHF≌△AHC(ASA).
∴AF＝AC，HF＝HC.
∵AC＝3，AB＝5，
∴AF＝AC＝3，BF＝AB－AF＝5－3＝2.
∵AD为△ABC的中线，
∴DH是△BCF的中位线.
∴DH＝eq \f(1,2)BF＝1.
22.证明：(1)∵BE，CF是△ABC的中线，
∴EF是△ABC的中位线，
∴EF∥BC且EF＝0.5BC．
∵P，Q分别是BG，CG的中点，
∴PQ是△BCG的中位线，
∴PQ∥BC且PQ＝0.5BC，
∴EF∥PQ且EF＝PQ．
∴四边形EFPQ是平行四边形．
(2)BG＝2GE．
23.解：当AC＝BD且AC⊥BD时，四边形EFGH是正方形.
理由如下：
在△ABC中，E、F分别是边AB、BC中点，
所以EF∥AC，且EF＝eq \f(1,2)AC，
同理有GH∥AC，且GH＝eq \f(1,2)AC，
∴EF∥GH且EF＝GH，
故四边形EFGH是平行四边形.
EH∥BD且EH＝BD，若AC＝BD，
则有EH＝EF，
又因为四边形EFGH是平行四边形，
∴四边形EFGH是菱形.
即：当AC＝BD且AC⊥BD时，四边形EFGH是正方形.
24.解：延长BE交AC于F
∵AE平分∠BAC
∴∠BAE＝∠CAE
∵BE⊥AE，AE＝AE
∴△ABE全等于△AFE
∴AF＝AB，BE＝EF
∵AB＝5
∴AF＝5
∵AC＝7
∴CF＝AC﹣AF＝7﹣5＝2
∵D为BC中点
∴BD＝CD
∴DE是△BCF的中位线
∴DE＝eq \f(1,2)CF＝1
25.解：(1)四边形EFGH的形状是平行四边形．理由如下：如图1，连结BD．
∵E、H分别是AB、AD中点，
∴EH∥BD，EH＝eq \f(1,2)BD，
同理FG∥BD，FG＝eq \f(1,2)BD，
∴EH∥FG，EH＝FG，
∴四边形EFGH是平行四边形；
(2)当四边形ABCD的对角线满足互相垂直的条件时，四边形EFGH是矩形．理由如下：
如图2，连结AC、BD．
∵E、F、G、H分别为四边形ABCD四条边上的中点，
∴EH∥BD，HG∥AC，
∵AC⊥BD，
∴EH⊥HG，
又∵四边形EFGH是平行四边形，
∴平行四边形EFGH是矩形；
(3)菱形的中点四边形是矩形．理由如下：
如图3，连结AC、BD．
∵E、F、G、H分别为四边形ABCD四条边上的中点，
∴EH∥BD，HG∥AC，FG∥BD，EH＝eq \f(1,2)BD，FG＝eq \f(1,2)BD，
∴EH∥FG，EH＝FG，
∴四边形EFGH是平行四边形．
∵四边形ABCD是菱形，
∴AC⊥BD，
∵EH∥BD，HG∥AC，
∴EH⊥HG，
∴平行四边形EFGH是矩形．
故答案为：平行四边形；互相垂直．