






所属成套资源:中考数学优化探究一轮复习精品课件(理数)
中考数学优化探究一轮复习(理数) 第2章 专题提能 函数与导数综合问题的突破策略课件PPT
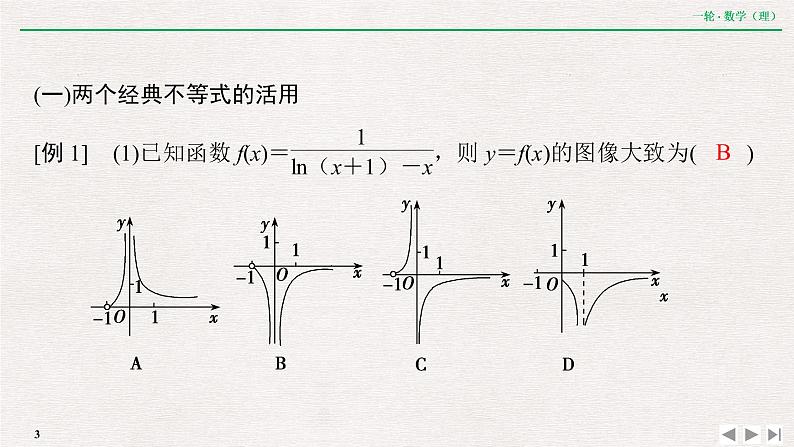
展开冲刺高考 金榜题名2023届优化探究一轮复习(理数)第二章 函数、导数及其应用专题提能 函数与导数综合问题的突破策略B 利用两个经典不等式解决其他问题,降低了思考问题的难度,优化了推理和运算过程.(1)对数形式:x≥1+ln x(x>0),当且仅当x=1时,等号成立.(2)指数形式:ex≥x+1(x∈R),当且仅当x=0时,等号成立.进一步可得到一组不等式链:ex>x+1>x>1+ln x(x>0,且x≠1). 通过二次求导,我们判断出了第一次求导中的导函数的符号,并最终解决了问题.2.“二次求导”与证明问题[例4] 已知函数f(x)=xln x-ex+1.(1)求曲线y=f(x)在点(1,f(1))处的切线方程;(2)证明:f(x)<sin x在(0,+∞)上恒成立.[解析] (1)依题意得f′(x)=ln x+1-ex,又f(1)=1-e,f′(1)=1-e,故所求切线方程为y-1+e=(1-e)(x-1),即y=(1-e)x.(2)证明:依题意,要证f(x)<sin x,即证xln x-ex+1<sin x,即证xln x<ex+sin x-1.当0<x≤1时,ex+sin x-1>0,xln x≤0,故xln x<ex+sin x-1,即f(x)<sin x.当x>1时,令g(x)=ex+sin x-1-xln x,故g′(x)=ex+cos x-ln x-1,令h(x)=g′(x)=ex+cos x-ln x-1, 故h(x)在(1,+∞)上单调递增.故h(x)>h(1)=e+cos 1-1>0,即g′(x)>0,所以g(x)在(1,+∞)上单调递增,所以g(x)>g(1)=e+sin 1-1>0,即xln x<ex+sin x-1,即f(x)<sin x.综上所述,f(x)<sin x在(0,+∞)上恒成立.本题是应用导数证明不等式.证明的关键在于构造适当的函数,然后在相应区间上用二次求导的办法判定导数的符号,获得函数的单调性,再利用单调性证明不等式.(三)消元消参巧构造、妙解极值点偏移问题1.极值点偏移的含义、判定极值点偏移的含义若单峰函数f(x)的极值点为x0,则极值点的偏移问题的图示及函数值的大小关系如下表所示. 该题直接利用极值点偏移的一般解法,根据所证不等式的结构特征,先把两个变量分到不等号的两边,再利用已知函数的单调性,将其转化为函数值的大小比较问题,进而直接构造相应函数F(x)=f(x)+f(2-x),x∈(0,1).这也是解决此类问题最为直接的方法,渗透了对数学建模等核心素养的考查.





