2023高考数学复习专项训练《点面距离》

这是一份2023高考数学复习专项训练《点面距离》，共23页。试卷主要包含了、单选题，、多选题，、填空题，、解答题等内容，欢迎下载使用。

一 、单选题（本大题共8小题，共40分）
1.（5分）在四面体ABCD中，E，F分别是AB，CD的中点，若AC⊥BD，且AC=4，BD=3，则EF=（ ）
A. 5B. 4C. 3D. 2.5
2.（5分）如图，在棱长为1的正方体ABCD-A1B1C1D1中，P为棱CC1上的动点(包含端点C1)，过点P作平面α分别与棱BC，CD交于M，N两点，若CP=2CM=2CN，则下列说法正确的是( )
A. 当点P与C1重合时，直线A1C与平面α的交点恰好是ΔPMN的重心
B. 存在点P，使得A1C⊥平面α
C. 点A1到平面α的距离最小为43
D. 用过P，M，A三点的平面截正方体，所得截面与棱A1D1的交点随点P而改变
3.（5分）在中，，，则面积为( )
A. B. C. D.
4.（5分）点P（a，b，c）关于xOy平面的对称点的坐标为（ ）
A. （a，b，-c）B. （-a，b，c）
C. （a，-b，c）D. （-a，-b，c）
5.（5分）点P是等腰三角形ABC所在平面外一点，PA⊥平面ABC，PA=8，在ΔABC中，BC=6，AB=AC=5，则点P到BC的距离是( )
A. 45B. 3C. 33D. 23
6.（5分）P为四棱锥S-ABCD的面SBC内一点，若动点P到平面abc的距离与到点S的距离相等，则动点P的轨迹是面SBC内( )
A. 线段或圆的一部分B. 双曲线或椭圆的一部分
C. 双曲线或抛物线的一部分D. 抛物线或椭圆的一部分
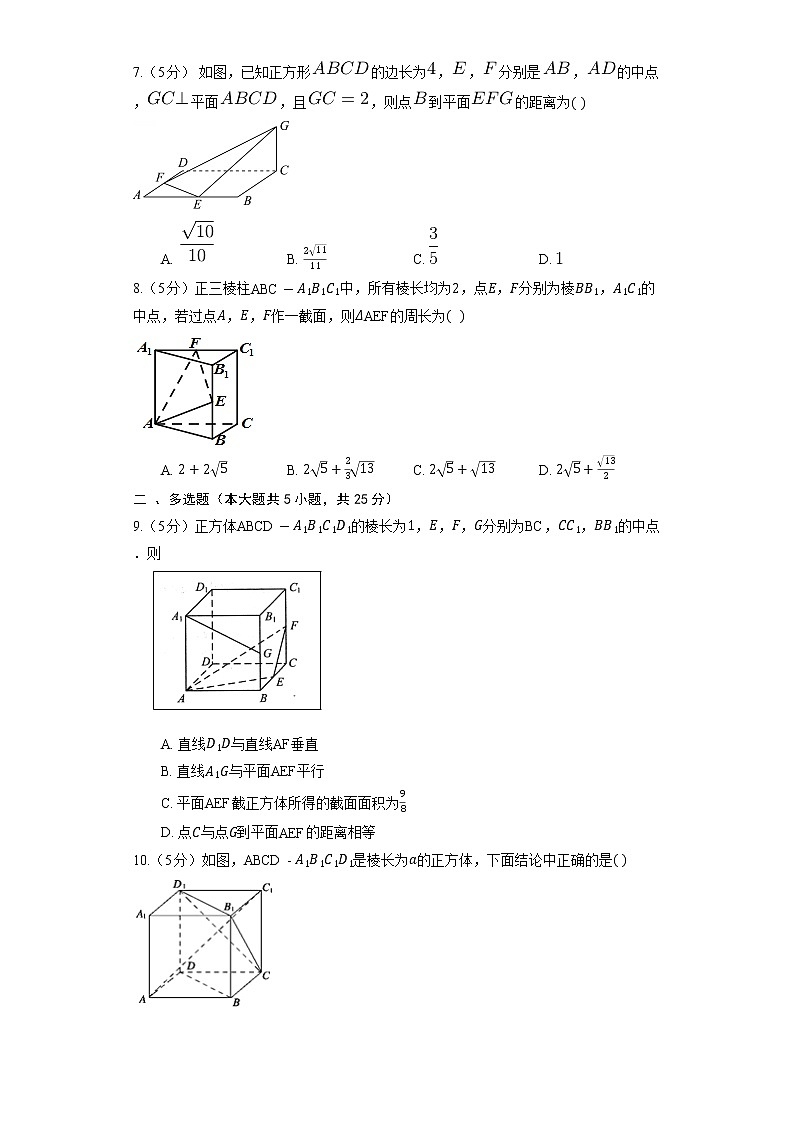
7.（5分） 如图，已知正方形的边长为，，分别是，的中点，平面，且，则点到平面的距离为( )
A. B. 21111C. D.
8.（5分）正三棱柱ABC-A1B1C1中，所有棱长均为2，点E，F分别为棱BB1，A1C1的中点，若过点A，E，F作一截面，则ΔAEF的周长为( )
A. 2+25B. 25+2313C. 25+13D. 25+132
二 、多选题（本大题共5小题，共25分）
9.（5分）正方体ABCD-A1B1C1D1的棱长为1，E，F，G分别为BC，CC1，BB1的中点．则
A. 直线D1D与直线AF垂直
B. 直线A1G与平面AEF平行
C. 平面AEF截正方体所得的截面面积为98
D. 点C与点G到平面AEF的距离相等
10.（5分）如图，ABCD-A1B1C1D1是棱长为a的正方体，下面结论中正确的是( )

A. AC1//平面CB1D1B. C1点到平面CB1D1的距离为33a
C. AC1与底面ABCD所成角的正切值是22D. 异面直线CD1与BD所成角为π3.
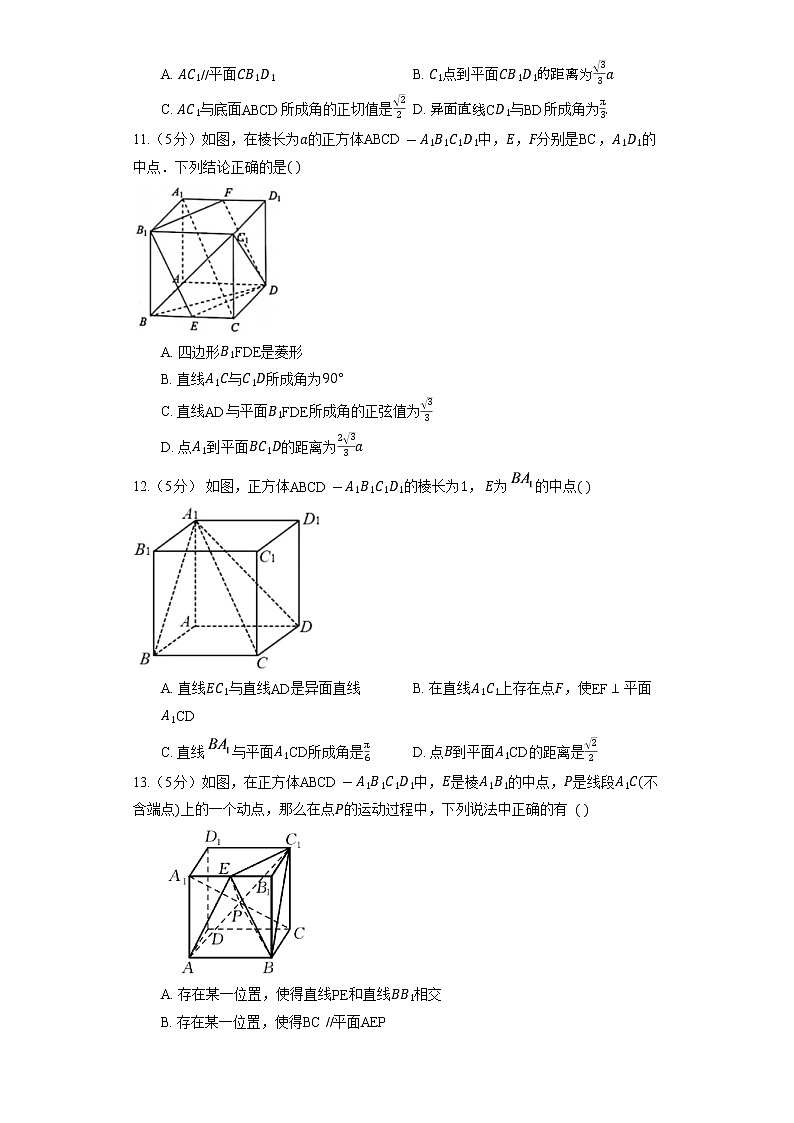
11.（5分）如图，在棱长为a的正方体ABCD-A1B1C1D1中，E，F分别是BC，A1D1的中点．下列结论正确的是( )
A. 四边形B1FDE是菱形
B. 直线A1C与C1D所成角为90°
C. 直线AD与平面B1FDE所成角的正弦值为33
D. 点A1到平面BC1D的距离为233a
12.（5分） 如图，正方体ABCD-A1B1C1D1的棱长为1， E为的中点( )
A. 直线EC1与直线AD是异面直线B. 在直线A1C1上存在点F，使EF⊥平面A1CD
C. 直线与平面A1CD所成角是π6D. 点B到平面A1CD的距离是22
13.（5分）如图，在正方体ABCD-A1B1C1D1中，E是棱A1B1的中点，P是线段A1C(不含端点)上的一个动点，那么在点P的运动过程中，下列说法中正确的有 ( )
A. 存在某一位置，使得直线PE和直线BB1相交
B. 存在某一位置，使得BC //平面AEP
C. 点A1与点B1到平面PBE的距离总相等
D. 三棱锥C1-PBE的体积不变
三 、填空题（本大题共5小题，共25分）
14.（5分）在棱长为a的正方体ABCD-A1B1C1D1中，点A到平面BB1C1C的距离为 ______ ，点A到平面BB1D1D的距离为 ______ ，AA1到平面BB1D1D的距离为 ______ ．
15.（5分）如图所示的多面体是由底面为的长方体被截面 所截而得到的，其中 .则点 到平面 的距离为 ．

16.（5分）正方形ABCD的边长为12cm，PA⊥平面ABCD，且PA=12cm，则点P到BD的距离为__________.
17.（5分）如图，在三棱锥P-ABC中，AB=AC=5，BC=6，PA⊥平面ABC，PA=8，则点P到BC的距离是_________.
18.（5分）ΔABC的顶点为A(4,1,9)，B(10,-1,6)，C(2,4,3)，则ΔABC的形状是________.
四 、解答题（本大题共5小题，共60分）
19.（12分）在三棱锥P-ABE中，PA⊥底面ABE，AB⊥AE，AB=AP=12AE=2，D是AE的中点，C是线段BE上的一点，且AC=5，连接PC，PD，CD．
(1)求证：CD//平面PAB；
(2)求点E到平面PCD的距离．
20.（12分）如图，AD⊥面ABE， 四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE.
(Ⅰ)求证：AE⊥平面BCE；
(Ⅱ)求点D到平面ACE的距离.
21.（12分）如图，在多面体ABCDM中，ΔBCD是等边三角形，ΔCMD是等腰直角三角形，∠CMD=90°，平面CMD⊥平面BCD，AB⊥平面BCD.

(1)求证：CD⊥AM;(2)若AM=BC=2，求点M到平面ABD的距离和点A到平面BDM的距离.
22.（12分）如图，在四棱锥S-ABCD中，SD⊥底面ABCD，底面ABCD是正方形，且SD=AD，E是SA的中点．

(Ⅰ)求证：直线BA⊥平面SAD；
(Ⅱ)求直线SA与平面BED的夹角的正弦值．
23.（12分）已知在如图所示的几何体中，∠BAC=90°，PA⊥平面ABC，AB=3，AC=4，PA=2.若M是BC的中点，且PQ//AC，QM//平面PAB.
(1)求线段PQ的长度；
(2)求三棱锥Q-AMC的体积V.
答案和解析
1.【答案】D;
【解析】解：如图所示，取AD的中点M，连接ME、MF．又E，F分别是AB，CD的中点．
由三角形的中位线定理可得：ME∥.
BD，MF∥.
AC．
∵AC⊥BD，且AC=4，BD=3，
∴ME⊥MF，ME=
，MF=2，
在△MEF中，由勾股定理可得：EF=22+(
)2=2.5．
故选D．
2.【答案】C;
【解析】
此题主要考查空间向量法研究线面位置关系及点面距等，属中档题目.
建立空间直角坐标系，利用空间向量法研究线面位置关系及点面距.

解：如图，以C为原点建立空间直角坐标系，
设CP=t，因此P(0,0,t)，M(0,t2,0)，N(t2,0,0)，
由此ΔPMN的重心为G(t6,t6,t3)，CG→=(t6,t6,t3)，
C→A1=(1,1,1)，
当CP=t=1时，CG→=(16,16,13)与C→A1=(1,1,1)不平行，因此选项A错误；
PM→=(t2,0,-t)，从而PM→.C→A1=-t2≠0对0