【中考一轮复习】2023年中考数学人教版单元检测卷——专题25 概率初步（原卷版+解析版）

这是一份【中考一轮复习】2023年中考数学人教版单元检测卷——专题25 概率初步（原卷版+解析版），文件包含中考一轮复习2023年中考数学人教版单元检测卷专题26反比例函数解析版doc、中考一轮复习2023年中考数学人教版单元检测卷专题26反比例函数原卷版doc等2份试卷配套教学资源，其中试卷共34页， 欢迎下载使用。

（试卷满分120分，答题时间120分钟）
一、选择题（共10小题，每题3分，共30分）
1. （2022广西贺州）已知一次函数的图象如图所示，则与的图象为（ ）
A. B. C. D.
【答案】A
【解析】根据题意可得，从而得到一次函数的图象经过第一、二、四象限，反比函数的图象位于第一、三象限内，即可求解．
根据题意得：，
∴，
∴一次函数的图象经过第一、二、四象限，反比函数的图象位于第一、三象限内．
故选：A
【点睛】本题主要考查了一次函数和反比例函数的图象和性质，熟练掌握一次函数和反比例函数的图象和性质是解题的关键．
2. （2022山东日照）如图，矩形OABC与反比例函数（k1是非零常数，x>0）的图象交于点M，N，与反比例函数（k2是非零常数，x>0）的图象交于点B，连接OM，ON．若四边形OMBN的面积为3，则k1-k2=（ ）
A. 3B. -3C. D.
【答案】B
【解析】根据矩形的性质以及反比例函数系数k的几何意义即可得出结论．
∵点M、N均是反比例函数（k1是非零常数，x>0）的图象上，
∴，
∵矩形OABC的顶点B在反比例函数（k2是非零常数，x>0）的图象上，
∴S矩形OABC=k2，
∴S四边形OMBN=S矩形OABC-S△OAM-S△OCN=3，
∴k2-k1=3，
∴k1-k2=-3，
故选：B．
【点睛】本题考查了矩形的性质，反比例函数系数k的几何意义：在反比例函数图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．
3. （2022广东）点，，，在反比例函数图象上，则，，，中最小的是（ ）
A. B. C. D.
【答案】D
【解析】根据反比例函数的性质可直接进行求解．
由反比例函数解析式可知：，
∴在每个象限内，y随x的增大而减小，
∵点，，，在反比例函数图象上，
∴，
故选D．
【点睛】本题主要考查反比例函数的性质，熟练掌握反比例函数的性质是解题的关键．
4.（2022海南）若反比例函数的图象经过点，则它的图象也一定经过的点
是（ ）
A. B. C. D.
【答案】C
【解析】【分析】先利用反比例函数的图象经过点，求出k的值，再分别计算选项中各点的横纵坐标之积，然后根据反比例函数图象上点的坐标特征进行判断．
∵反比例函数的图象经过点，
∴k＝2×（﹣3）＝﹣6，
∵（﹣2）×（﹣3）＝6≠﹣6，
（﹣3）×（﹣2）＝6≠﹣6，
1×（﹣6）＝﹣6，
,6×1＝6≠﹣6，
则它一定还经过（1，﹣6），
故选：C．
【点睛】本题考查了反比例函数图象上点的坐标特征：反比例函数的图象是双曲线，图象上的点（x，y）的横纵坐标的积是定值k，即xy＝k．熟练掌握反比例函数的性质是解题的关键．
5. （2022长春）如图，在平面直角坐标系中，点P在反比例函数（，）的图象上，其纵坐标为2，过点P作//轴，交x轴于点Q，将线段绕点Q顺时针旋转60°得到线段．若点M也在该反比例函数的图象上，则k的值为（ ）
A. B. C. D. 4
【答案】C
【解析】作MN⊥x轴交于点N，分别表示出ON、MN，利用k值的几何意义列式即可求出结果．
作MN⊥x轴交于点N，如图所示，
∵P点纵坐标为：2，
∴P点坐标表示为：（，2），PQ=2，
由旋转可知：QM=PQ=2，∠PQM=60°，
∴∠MQN=30°，
∴MN=，QN=，
∴，
即：，
解得：k=，
故选：C．
【点睛】本题主要考查的是k的几何意义，表示出对应线段是解题的关键．
6. （2022湖南邵阳）如图是反比例函数y=的图象，点A(x，y)是反比例函数图象上任意一点，过点A作AB⊥x轴于点B，连接OA，则△AOB的面积是（ ）
A. 1B. C. 2D.
【答案】B
【解析】由反比例函数的几何意义可知，k=1，也就是△AOB的面积的2倍是1，求出△AOB的面积是．
设A（x，y）则OB=x，AB=y，
∵A为反比例函数y=图象上一点，
∴xy=1，
∴S△ABO=AB•OB=xy=×1=，
【点睛】考查反比例函数的几何意义，即k的绝对值，等于△AOB的面积的2倍，数形结合比较直观．
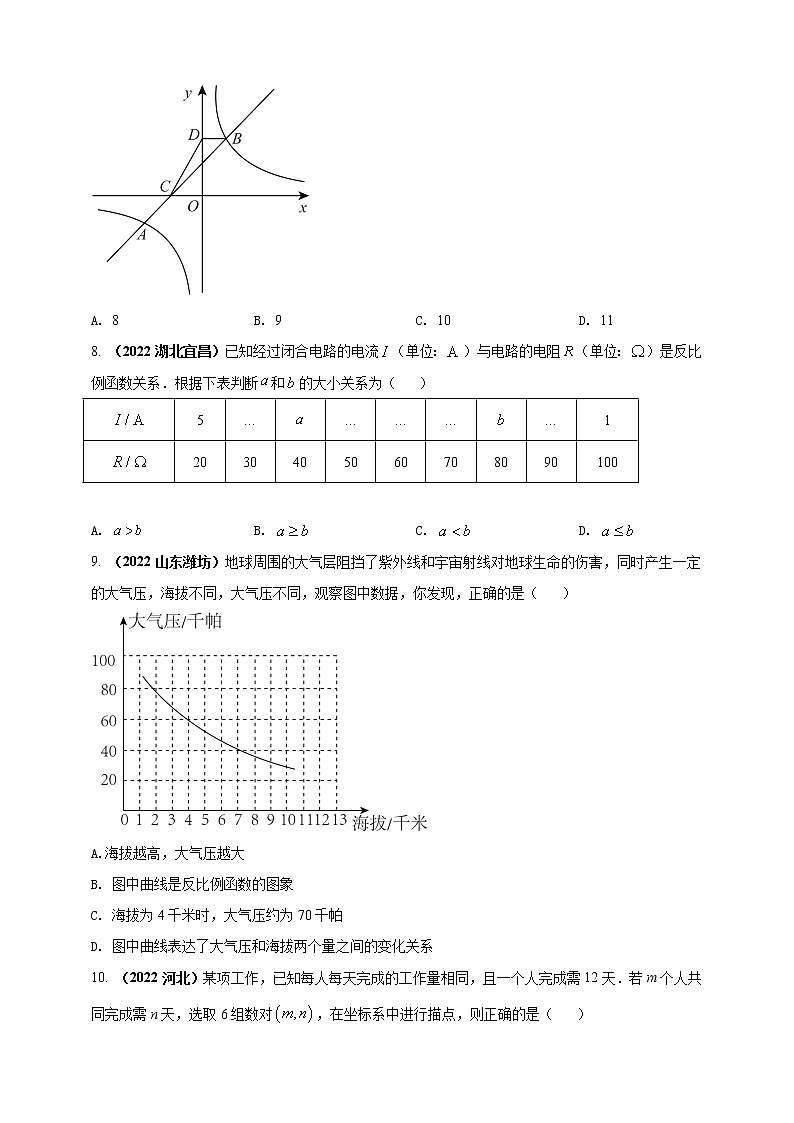
7. （2022湖南怀化）如图，直线AB交x轴于点C，交反比例函数y＝（a＞1）的图像于A、B两点，过点B作BD⊥y轴，垂足为点D，若S△BCD＝5，则a的值为（ ）
A. 8B. 9C. 10D. 11
【答案】D
【解析】设，由S△BCD=即可求解.
设，
∵BD⊥y轴
∴S△BCD==5，
解得：
【点睛】本题主要考查反比例函数的应用，掌握反比例函数的相关知识是解题的关键．
8. （2022湖北宜昌）已知经过闭合电路的电流（单位：）与电路的电阻（单位：）是反比例函数关系．根据下表判断和的大小关系为（ ）
A. B. C. D.
【答案】A
【解析】根据电流与电路的电阻是反比例函数关系，由反比例函数图像是双曲线，在同一象限内x和y的变化规律是单调的，即可判断
∵电流与电路的电阻是反比例函数关系
由表格：；
∴在第一象限内，I随R的增大而减小
∵
∴
【点睛】本题考查双曲线图像的性质；解题关键是根据表格判断出双曲线在第一象限，单调递减.
9. （2022山东潍坊）地球周围的大气层阻挡了紫外线和宇宙射线对地球生命的伤害，同时产生一定的大气压，海拔不同，大气压不同，观察图中数据，你发现，正确的是（ ）
A.海拔越高，大气压越大
B. 图中曲线是反比例函数的图象
C. 海拔为4千米时，大气压约为70千帕
D. 图中曲线表达了大气压和海拔两个量之间的变化关系
【答案】D
【解析】根据图象中的数据回答即可．
A．海拔越高，大气压越小，该选项不符合题意；
B．∵图象经过点(2，80)，(4，60)，
∴2×80=160，4×60=240，而160≠240，
∴图中曲线不是反比例函数的图象，该选项不符合题意；
C．∵图象经过点 (4，60)，
∴海拔为4千米时，大气压约为60千帕，该选项不符合题意；
D．图中曲线表达了大气压和海拔两个量之间的变化关系，该选项符合题意.
【点睛】本题考查了函数的图象，解题的关键是读懂题意，能正确识图．
10. （2022河北）某项工作，已知每人每天完成的工作量相同，且一个人完成需12天．若m个人共同完成需n天，选取6组数对，在坐标系中进行描点，则正确的是（ ）
A. B.
C D.
【答案】C
【解析】根据题意建立函数模型可得，即，符合反比例函数，根据反比例函数的图象进行判断即可求解．
依题意，
，
，且为整数．
【点睛】本题考查了反比例数的应用，根据题意建立函数模型是解题的关键．
二、填空题（共10小题，每空3分，共33分）
1. （2022北京）在平面直角坐标系中，若点在反比例函数的图象上，则______（填“>”“=”或“<”）
【答案】＞
【解析】根据反比例函数的性质，k>0，在每个象限内，y随x的增大而减小，进行判断即可．
∵k>0，
∴在每个象限内，y随x的增大而减小，
，
∴>．
【点睛】本题考查了反比例函数的性质，熟练掌握函数的性质是解决问题的关键．
2. （2022广西河池）如图，点P（x，y）在双曲线的图象上，PA⊥x轴，垂足为A，若S△AOP＝2，则该反比例函数的解析式为 _____．
【答案】
【解析】根据反比例函数比例系数的几何意义，即可求解．
根据题意得：，
∴，
∵图象位于第二象限内，
∴，
∴该反比例函数解析式为．
【点睛】本题主要考查了反比例函数比例系数的几何意义，熟练掌握反比例函数比例系数的几何意义是解题的关键．
3. （2022山东济宁）如图，A是双曲线上的一点，点C是OA的中点，过点C作y轴的垂线，垂足为D，交双曲线于点B，则△ABD的面积是___________．
【答案】4
【解析】根据点C是OA的中点，根据三角形中线的可得S△ACD = S△OCD, S△ACB = S△OCB,进而可得S△ABD = S△OBD,根据点B在双曲线上，BD⊥ y轴，可得S△OBD=4，进而即可求解．
【详解】点C是OA的中点，
∴S△ACD = S△OCD, S△ACB = S△OCB,
∴S△ACD + S△ACB = S△OCD + S△OCB,
∴S△ABD = S△OBD,
点B在双曲线上，BD⊥ y轴，
∴S△OBD=×8=4,
∴S△ABD =4,
答案为：4.
【点睛】本题考查了三角形中线的性质，反比例函数的的几何意义，掌握反比例函数的几何意义是解题的关键．
4. （2022浙江绍兴）如图，在平面直角坐标系xOy中，点（0，4），（3，4），将向右平移到位置，的对应点是，的对应点是，函数的图象经过点和的中点，则的值是______．
【答案】6
【解析】【分析】作FG⊥x轴，DQ⊥x轴，FH⊥y轴，设AC=EO=BD=a，表示出四边形ACEO的面积，再根据三角形中位线的性质得出FG，EG，即可表示出四边形HFGO的面积，然后根据k的几何意义得出方程，求出a，可得答案．
【详解】过点F作FG⊥x轴，DQ⊥x轴，FH⊥y轴，根据题意，得AC=EO=BD，
设AC=EO=BD=a，
∴四边形ACEO的面积是4a．
∵F是DE的中点，FG⊥x轴，DQ⊥x轴，
∴FG是△EDQ的中位线，
∴，，
∴四边形HFGO的面积为，
∴，
解得，
∴k=6．
故答案为：6．
【点睛】本题主要考查了反比例函数中k的几何意义，正确的作出辅助线构造矩形是解题的关键．
5. （2022浙江湖州）如图，已知在平面直角坐标系xOy中，点A在x轴的负半轴上，点B在y轴的负半轴上，，以AB为边向上作正方形ABCD．若图像经过点C的反比例函数的解析式是，则图像经过点D的反比例函数的解析式是______．
【答案】
【解析】过点C作CE⊥y轴于点E，过点D作DF⊥x轴于点F，设，，结合正方形的性质，全等三角形的判定和性质，得到≌≌，然后表示出点C和点D的坐标，求出，即可求出答案．
过点C作CE⊥y轴于点E，过点D作DF⊥x轴于点F，如图：
∵，
设，，
∴点A为（，0），点B为（0，）；
∵四边形ABCD是正方形，
∴，，
∴，
∴，
同理可证：，
∵，
∴≌≌，
∴，，
∴，
∴点C的坐标为（，），点D的坐标为（，），
∵点C在函数函数图像上，
∴，即；
∴，
∴经过点D的反比例函数解析式为；
故答案为：．
【点睛】本题考查了正方形的性质，全等三角形的判定和性质，反比例函数的性质，三角函数，余角的性质等知识，解题的关键是熟练掌握所学的知识，正确的表示出点C和点D的坐标，从而进行解题．
6. （2022安徽）如图，平行四边形OABC的顶点O是坐标原点，A在x轴的正半轴上，B，C在第一象限，反比例函数的图象经过点C，的图象经过点B．若，则________．
【答案】3
【解析】【分析】过点C作CD⊥OA于D，过点B作BE⊥x轴于E，先证四边形CDEB为矩形，得出CD=BE，再证Rt△COD≌Rt△BAE（HL），根据S平行四边形OCBA=4S△OCD=2，再求S△OBA=即可．
详解】过点C作CD⊥OA于D，过点B作BE⊥x轴于E，
∴CD∥BE，
∵四边形ABCO为平行四边形，
∴CB∥OA，即CB∥DE，OC=AB，
∴四边形CDEB为平行四边形，
∵CD⊥OA，
∴四边形CDEB为矩形，
∴CD=BE，
∴在Rt△COD和Rt△BAE中，
，
Rt△COD≌Rt△BAE（HL），
∴S△OCD=S△ABE，
∵OC=AC，CD⊥OA，
∴OD=AD，
∵反比例函数的图象经过点C，
∴S△OCD=S△CAD=，
∴S平行四边形OCBA=4S△OCD=2，
∴S△OBA=，
∴S△OBE=S△OBA+S△ABE=，
∴．
故答案为3．
【点睛】本题考查反比例函数k的几何意义，平行四边形的性质与判定，矩形的判定与性质，三角形全等判定与性质，掌握反比例函数k的几何意义，平行四边形的性质与判定，矩形的判定与性质，三角形全等判定与性质．
7. （2022浙江宁波）如图，四边形OABC为矩形，点A在第二象限，点A关于OB的对称点为点D，点B，D都在函数的图象上，BE⊥x轴于点E．若DC的延长线交x轴于点F，当矩形OABC的面积为时，的值为___________，点F的坐标为___________．
【答案】 ①. ②. （，0）
【解析】【分析】连接OD，作DG⊥x轴，设点B（b，），D（a，），根据矩形的面积得出三角形BOD的面积，将三角形BOD的面积转化为梯形BEGD的面积，从而得出a，b的等式，将其分解因式，从而得出a，b的关系，进而在直角三角形BOD中，根据勾股定理列出方程，进而求得B，D的坐标，进一步可求得结果．
【详解】解：如图，
作DG⊥x轴于G，连接OD，设BC和OD交于I，
设点B（b，），D（a，），
由对称性可得：△BOD≌△BOA≌△OBC，
∴∠OBC=∠BOD，BC=OD，
∴OI=BI，
∴DI=CI，
∴，
∵∠CID=∠BIO，
∴△CDI∽△BOI，
∴∠CDI=∠BOI，
∴CD∥OB，
∴S△BOD=S△AOB=S矩形AOCB=，
∵S△BOE=S△DOG=|k|=3，S四边形BOGD=S△BOD+S△DOG=S梯形BEGD+S△BOE，
∴S梯形BEGD=S△BOD=，
∴ (+)•（a-b）=，
∴2a2-3ab-2b2=0，
∴（a-2b）•（2a+b）=0，
∴a=2b，a=-（舍去），
∴D（2b，），即：（2b，），
在Rt△BOD中，由勾股定理得，
OD2+BD2=OB2，
∴[（2b）2+（）2]+[（2b-b）2+（-）2]=b2+（）2，
∴b=，
∴B（，2），D（2，），
∵直线OB的解析式为：y=2x，
∴直线DF的解析式为：y=2x-3，
当y=0时，2x-3=0，
∴x=，
∴F（，0），
∵OE=，OF=，
∴EF=OF-OE=，
∴，
故答案为：，（，0）．
【点睛】本题考查了矩形性质，轴对称性质，反比例函数的“k”的几何含义，勾股定理，一次函数及其图象性质，分解因式等知识，解决问题的关键是变形等式，进行分解因式．
8. （2022湖南株洲）如图所示，矩形顶点、在轴上，顶点在第一象限，轴为该矩形的一条对称轴，且矩形的面积为6．若反比例函数的图象经过点，则的值为_________．
【答案】3
【解析】由图得，轴把矩形平均分为两份，即可得到上半部分的面积，利用矩形的面积公式即，又由于点C在反比例函数图象上，则可求得答案．
【详解】解：轴为该矩形的一条对称轴，且矩形的面积为6，
，
，
故答案为3．
【点睛】本题考查了反比例函数k的几何意义，熟练掌握是解题的关键．
9. （2022贵州遵义）反比例函数与一次函数交于点，则的值为_____．
【答案】6
【解析】将点，代入，求得，进而即可求解．
将点，代入，
即，
，
，
故答案为：6．
【点睛】本题考查了一次函数与反比例函数综合，求得点的坐标是解题的关键．
10. （2022陕西）已知点A(−2，m)在一个反比例函数的图象上，点A′与点A关于y轴对称．若点A′在正比例函数的图象上，则这个反比例函数的表达式为_______．
【答案】y=
【解析】根据点A与点A′关于y轴对称，得到A′(2，m)，由点A′在正比例函数的图象上，求得m的值，再利用待定系数法求解即可．
∵点A与点A′关于y轴对称，且A(−2，m)，
∴A′(2，m)，
∵点A′在正比例函数的图象上，
∴m=×2，
解得：m=1，
∴A(−2，1)，
设这个反比例函数的表达式为y=，
∵A(−2，1) 在这个反比例函数的图象上，
∴k=-2×1=-2，
∴这个反比例函数的表达式为y=，
故答案为：y=．
【点睛】本题考查反比例函数图象上点的坐标特征、关于x轴、y轴对称的点的坐标特征，解答本题的关键是明确题意，求出m的值．
三、解答题（本大题有6道小题，共57分）
1. （8分）（2022浙江金华）如图，点A在第一象限内，轴于点B，反比例函数的图象分别交于点C，D．已知点C的坐标为．
（1）求k的值及点D的坐标．
（2）已知点P在该反比例函数图象上，且在的内部（包括边界），直接写出点P的横坐标x的取值范围．
【答案】（1），； （2）；
【解析】【分析】（1）由C点坐标可得k，再由D点纵坐标可得D点横坐标；
（2）由C、D两点的横坐标即可求得P点横坐标取值范围；
【小问1详解】
解：把C（2，2）代入，得，，
∴反比例函数函数为（x＞0），
∵AB⊥x轴，BD=1，
∴D点纵坐标为1，
把代入，得，
∴点D坐标为（4，1）；
【小问2详解】
解：∵P点在点C（2，2）和点D（4，1）之间，
∴点P的横坐标：；
【点睛】本题考查了反比例函数解析式，坐标的特征，数形结合是解题关键．
2.（9分） （2022广西百色）已知：点 A（1，3）是反比例函数（k≠0）的图象与直线（ m≠0）的一个交点．
（1）求k 、m的值：
（2）在第一象限内，当时，请直接写出x的取值范围
【答案】（1） （2）
【解析】【分析】（1）把点A（1，3）分别代入和，求解即可；
（2）直接根据图象作答即可．
【详解】（1）点A（1，3）是反比例函数（k≠0）的图象与直线（m≠0）的一个交点，
把点A（1，3）分别代入和，
得，
；
（2）第一象限内，，
由图像得．
【点睛】本题考查了待定系数法求反比例函数和正比例函数解析式，图象法解不等式，熟练掌握知识点并能够运用数形结合的思想是解题的关键．
3. （10分）（2022甘肃威武）如图，B，C是反比例函数y=（k≠0）在第一象限图象上的点，过点B的直线y=x-1与x轴交于点A，CD⊥x轴，垂足为D，CD与AB交于点E，OA=AD，CD=3．
（1）求此反比例函数的表达式；
（2）求△BCE的面积．
【答案】（1） （2）1
【解析】【分析】（1）根据直线y=x-1求出点A坐标，进而确定OA，AD的值，再确定点C的坐标，代入反比例函数的关系式即可；
（2）求出点E坐标，进而求出EC，再求出一次函数与反比例函数在第一象限的交点B的坐标，由三角形的面积的计算方法进行计算即可．
【详解】（1）解：当y=0时，即x-1=0，
∴x=1，
即直线y=x-1与x轴交于点A的坐标为（1，0），
∴OA=1=AD，
又∵CD=3，
∴点C的坐标为（2，3），
而点C（2，3）在反比例函数y=的图象上，
∴k=2×3=6，
∴反比例函数的图象为y=；
（2）解：方程组的正数解为，
∴点B坐标为（3，2），
当x=2时，y=2-1=1，
∴点E的坐标为（2，1），即DE=1，
∴EC=3-1=2，
∴S△BCE=×2×（3-2）=1，
答：△BCE的面积为1．
【点睛】考查反比例函数、一次函数交点坐标以及待定系数法求函数关系式，将一次函数、反比例函数的关系式联立方程组是求出交点坐标的基本方法，将点的坐标转化为线段的长是正确解答的关键．
4. （10分）（2022重庆）已知一次函数的图象与反比例函数的图象相交于点，．
（1）求一次函数的表达式，并在图中画出这个一次函数的图象；
（2）根据函数图象，直接写出不等式的解集；
（3）若点是点关于轴的对称点，连接，，求的面积．
【答案】（1），图见解析
（2）或 （3）12
【解析】【分析】（1）把，分别代入得到m，n的值，得到点A和点B的坐标，利用待定系数法求出一次函数的表达式，并画出图象即可；
（2）由函数图象可知，当 或时，一次函数的图象在反比例函数的图象的上方，即可得到答案；
（3）根据点是点关于轴的对称点，求出点C的坐标，得到BC的长，进一步求出三角形的面积即可．
【小问1详解】
解：把，分别代入得，
，，
解得m＝4，n＝﹣2，
∴ 点A（1，4），点B（﹣2，﹣2），
把点A（1，4），点B（﹣2，﹣2）代入一次函数得，
，
解得，
∴一次函数的表达式是y＝2x＋2，
这个一次函数的图象如图，
【小问2详解】
解：由函数图象可知，当 或时，一次函数的图象在反比例函数的图象的上方，
∴不等式的解集为或；
【小问3详解】
解：∵点是点关于轴的对称点，点B的坐标是（﹣2，﹣2），
∴点C的坐标是（2，﹣2），
∴BC＝2－（﹣2）＝4，
∴．
【点睛】此题是反比例函数与一次函数综合题，主要考查了待定系数法求函数解析式、一次函数与反比例函数的交点问题、三角形的面积，熟练掌握一次函数与反比例函数的性质是解题的关键．
5. （10分）（2022济南）如图，一次函数的图象与反比例函数的图象交于点，与y轴交于点B．
（1）求a，k的值；
（2）直线CD过点A，与反比例函数图象交于点C，与x轴交于点D，AC＝AD，连接CB．
①求△ABC的面积；
②点P在反比例函数的图象上，点Q在x轴上，若以点A，B，P，Q为顶点的四边形是平行四边形，请求出所有符合条件的点P坐标．
【答案】（1），； （2）①8；②符合条件的点坐标是和．
【解析】【分析】（1）将点代入，求出，即可得，将点代入，即可求出k；
（2）①如图，过A作轴于点，过作轴于点，交于点，求出，，得到CE，进一步可求出△ABC的面积；②设，．分情况讨论：ⅰ、当四边形为平行四边形时，ⅱ、当四边形为平行四边形时，计算即可．
【小问1详解】
解：将点代入，得，，
将点代入，得，
反比例函数的解析式为．
【小问2详解】
解：①如图，过A作轴于点，过作轴于点，交于点，
∴，
∵，
∴，
∴，
∴，
∴，
∴，
∴，
∴．
②分两种情况：设，．
ⅰ、如图，当四边形为平行四边形时，
∵点向下平移1个单位、向右平移个单位得到点，
∴点向下平移1个单位，向右平移个单位得到点，
∴，，
∴．
ⅱ、如图，当四边形为平行四边形时，
∵点向上平移1个单位，向左平移个单位得到点，
∴点向上平移1个单位，向左平移个单位得到点，
∴，，
∴．
综上所述，符合条件的点坐标是和．
【点睛】本题考查一次函数与反比例函数的综合，待定系数法求函数解析式，平行四边形的性质，解题的关键是掌握待定系数法求函数解析式，平行四边形的性质．
6. （10分）（2022广西柳州）如图，在平面直角坐标系中，一次函数y＝k1x+b（k1≠0）的图像与反比例函数y=（k2≠0）的图像相交于A（3，4），B（﹣4，m）两点．
（1）求一次函数和反比例函数的解析式；
（2）若点D在x轴上，位于原点右侧，且OA＝OD，求△AOD的面积．
【答案】（1）y＝x+1；
（2）△AOD的面积为10
【解析】【分析】(1)把点A的坐标代入反比例函数解析式求出值，从而得到反比例函数解析式，再把点B的坐标代入反比例函数解析式求出m的值，然后利用待定系数法求函数解析式求出一次函数解析式；
(2)利用勾股定理求得OA，即可求得OD的长度，然后利用三角形面积公式求得即可．
（1）∵反比例函数图像与一次函数图像相交于点A（3，4），B（﹣4，m），
，
解得k2＝12，
∴反比例函数解析式为，
，
解得m＝﹣3，
∴点B的坐标为（﹣4，﹣3），
，
解得，
∴一次函数解析式为y＝x+1．
（2）∵A（3，4），
，
∴OA＝OD，
∴OD＝5，
△的面积×5×4=10．
【点睛】本题是反比例函数图像与一次函数图像交点问题，考查了待定系数法求函数的解析式，反比例函数图像上点的坐标特征，勾股定理的应用以及三角形面积，根据交点A的坐标求出反比例函数解析式以及点B的坐标是解题的关键．
5
…
…
…
…
…
1
20
30
40
50
60
70
80
90
100