福建省龙岩市长汀县2022-2023学年八年级上学期期中质量抽查数学试卷(含答案)

2022-2023学年第一学期期中质量抽查

八年级数学试题

（考试时间：120分钟；满分150分）

一、选择题（每小题4分，共40分）

1.没有哪一门学科能像数学这样，利用如此多的符号图形，展现一系列完备且完美的世界．下面是由4个数学式子绘制成的完美曲线，其中不是轴对称图形的是

A.      B.      C.       D.

    笛卡尔心形线        三叶玫瑰形曲线        蝴蝶形曲线          太极曲线

2.一个三角形的两边长分别为3和5，则它的第三边不可能是

A．9 B．5 C．4 D．3

3.一个n边形的每个外角都是45°，则这个n边形的内角和是

A．1080° B．540° C．2700° D．2160°

4.如图是一副三角尺拼成的图案，则∠AEB的度数为

A．60° B．75° C．90° D．105°

5.如图，△ACE≌△DBF，若AD＝11cm，BC＝5cm，则AB长为

A．6cm B．3cm C．4cm D．7cm

6.一块三角形玻璃样板不慎被小强同学碰破，成了四片完整四碎片（如图所示），聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板．你认为下列四个答案中考虑最全面的是

A．带其中的任意两块去都可以         B．带1、2或2、3去就可以了 

C．带1、4或3、4去就可以了         D．带1、4或2、3或3、4去均可

7.根据下列条件，能画出形状、大小确定的三角形的是

A．BC＝6，∠BAC＝90°           B．AB＝4，AC＝5，∠ABC＝60° 

C．AB＝4，AC＝5，BC＝6       D．∠ABC＝60°，∠BAC＝100°，∠BCA＝20°

8.如图，用一把长方形直尺的一边压住射线OB，再用另一把完全相同的直尺的一边压住射线OA，两把直尺的另一边交于点P，则射线OP就是∠AOB角平分线的依据是

A．等腰三角形中线、角平分线、高线三线合一 

B．角平分线上的点到这个角两边的距离相等 

C．三角形三边垂直平分线的交点到三角形三顶点的距离相等 

D．在角的内部，到角两边距离相等的点在这个角的角平分线上

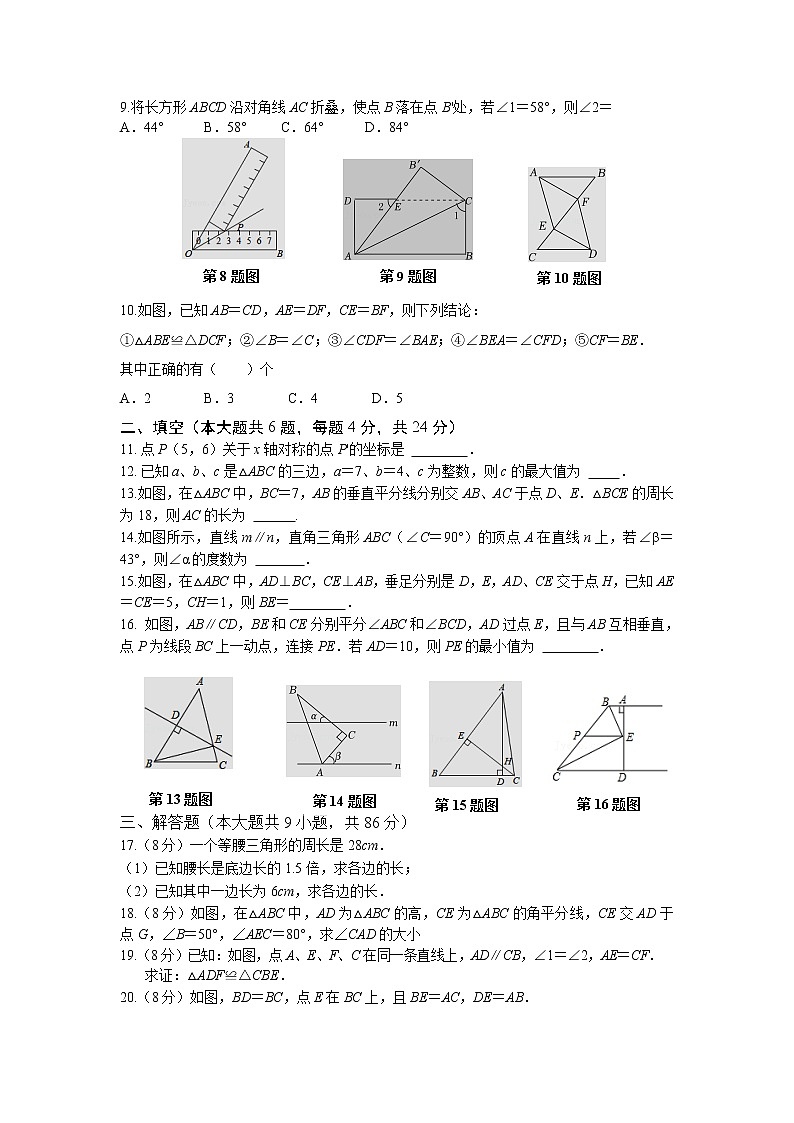
9.将长方形ABCD沿对角线AC折叠，使点B落在点B'处，若∠1＝58°，则∠2＝

A．44°    B．58°    C．64°    D．84°

10.如图，已知AB＝CD，AE＝DF，CE＝BF，则下列结论：

①△ABE≌△DCF；②∠B＝∠C；③∠CDF＝∠BAE；④∠BEA＝∠CFD；⑤CF＝BE．

其中正确的有（　　）个      

A．2     B．3     C．4     D．5

二、填空（本大题共6题，每题4分，共24分）

11. 点P（5，6）关于x轴对称的点P'的坐标是 　    　．
12. 已知a、b、c是△ABC的三边，a＝7、b＝4、c为整数，则c的最大值为 　 　．

13.如图，在△ABC中，BC＝7，AB的垂直平分线分别交AB、AC于点D、E．△BCE的周长为18，则AC的长为 　  　.

14.如图所示，直线m∥n，直角三角形ABC（∠C＝90°）的顶点A在直线n上，若∠β＝43°，则∠α的度数为 　   　．

15.如图，在△ABC中，AD⊥BC，CE⊥AB，垂足分别是D，E，AD、CE交于点H，已知AE＝CE＝5，CH＝1，则BE＝　    　．

16. 如图，AB∥CD，BE和CE分别平分∠ABC和∠BCD，AD过点E，且与AB互相垂直，点P为线段BC上一动点，连接PE．若AD＝10，则PE的最小值为 　    　．

三、解答题（本大题共9小题，共86分）

17.（8分）一个等腰三角形的周长是28cm．

（1）已知腰长是底边长的1.5倍，求各边的长；

（2）已知其中一边长为6cm，求各边的长．

18.（8分）如图，在△ABC中，AD为△ABC的高，CE为△ABC的角平分线，CE交AD于点G，∠B＝50°，∠AEC＝80°，求∠CAD的大小                                                   

19.（8分）已知：如图，点A、E、F、C在同一条直线上，AD∥CB，∠1＝∠2，AE＝CF．

求证：△ADF≌△CBE．

20.（8分）如图，BD＝BC，点E在BC上，且BE＝AC，DE＝AB．

（1）求证：△ABC≌△EDB；

（2）判断AC和BD的位置关系，并说明理由．

21.（8分）如图所示，在平面直角坐标系xOy中，△ABC的三个顶点坐标分别为A（1，1）B（4，2）C（2，3）．

（1）在图中画出△ABC关于x轴对称的图形△A1B1C1；

（2）在图中，若B2（﹣4，2）与点B关于一条直线成轴对称，则这条对称轴是　 　，此时C点关于这条直线的对称点C2的坐标为　 　    　；

（3）求△A1B1C1的面积．

22.（10分）如图，在等边△ABC中，点D在BC边上，点E在AC的延长线上，DE＝DA．

（1）求证：∠BAD＝∠EDC；

（2）作出点E关于直线BC的对称点M，

连接DM、AM，猜想DM与AM的数量

关系，并说明理由．

23.（10分）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝1．将三角板中30°角的顶点D放在AB边上移动，使这个30°角的两边分别与△ABC的边AC，BC相交于点E，F，且使DE始终与AB垂直．

（1）△BDF是什么三角形？请说明理由；

（2）设AD＝a，求CF的值（用含a的式子表示）；

（3）当移动点D使EF∥AB时，求AD的长．

24.（12分）在一个三角形中，如果一个角是另一个角的2倍，这样的三角形我们称之为“倍角三角形”．如图，△ABC中，∠ACB＝90°，点P是线段AB上一点（不与A、B重合），连接CP．（1）当∠B＝72°时；

①若∠CPB＝54°，则△ACP　 　“倍角三角形”（填“是”或“否”）；

②若△BPC是“倍角三角形”，求∠ACP的度数；

（2）当△ABC、△BPC、△ACP都是“倍角三角形”时，直接写出∠BCP的度数．

25.（14分）如图，在△ABC中，∠B＝90°，AB＝16cm，BC＝12cm，AC＝20cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．

（1）BP＝　     　（用t的代数式表示）

（2）当点Q在边BC上运动时，出发几秒后，△PQB是等腰三角形？

（3）当点Q在边CA上运动时，求出发几秒后，△BCQ是以BC或BQ为底边的等腰三角形？

2022-2023学年八年级上数学期中参考答案

一、选择题

二、填空题

11. （5，﹣6）.    12.  　10　.   13. 　11　.    14. 　47°　.  15. 　4　.  16. 　5　.

三、解答题

17.(8分)解：（1）设底边长为xcm，则腰长是1.5xcm，

x+1.5x+1.5x＝28，    …………2分

解得：x＝7，所以1.5x＝10.5（cm），…………3分

故，该等腰三角形的各边长为：7cm，10.5cm，10.5cm；…………4分

（2）若底边长为6cm，设腰长为ycm，

则：6+2y＝28，

得：y＝11，

∴三边长分别为：6cm，11cm，11cm， …………6分

若腰长为6cm，设底边长为acm，

则：6+6+a＝28，得a＝16，

又∵6+6＝12＜16，故舍去，…………7分

综上所述，该等腰三角形的三边长分别为：6cm，11cm，11cm．…………8分

18. (8分)解：∵∠AEC是△BCE的外角，

∴∠AEC＝∠B+∠BCE，    …………2分

∵∠B＝50°，∠AEC＝80°，

∴∠BCE＝∠AEC﹣∠B

＝80°﹣50°

＝30°，…………4分

∵CE是△ABC的角平分线，

∴∠ACB＝2∠BCE＝2×30°＝60°，…………5分

∵AD为△ABC的高，

∴∠ADC＝90°，                …………6分

∴∠CAD＝180°﹣∠ADC﹣∠ACB

＝180°﹣90°﹣60°

＝30°  …………8分

19. (8分)证明：∵AD∥CB，

∴∠A＝∠C，…………1分

∵AE＝CF，

∴AE+EF＝CF+EF，

∴AF＝CE，     …………3分

在△ADF和△CBE中，

，         …………7分

∴△ADF≌△CBE（ASA）．  …………8分

20 .(8分)（1）证明：在△ABC和△EDB中，

，  …………2分

∴△ABC≌△EDB（SSS）；………………4分

（2）AC∥BD，理由如下：…………5分

∵△ABC≌△EDB，…………6分

∴∠ACB＝∠EBD，………………7分

∴AC∥BD．……………………8分

21. （8分）解：（1）如图，△A1B1C1为所作；

………………3分

（2）这条对称轴是  y 轴，…………4分

C点的对称点C2的坐标为（﹣2，3）；…………5分

故答案为：y轴，（﹣2，3）；

（3）△A1B1C1的面积＝2×3﹣×2×1﹣×2×1﹣×1×3             

＝2.5．  …………8分

22. （10分）解：（1）如图1，∵△ABC是等边三角形，

∴∠BAC＝∠ACB＝60°．…………1分

又∵∠BAD+∠DAC＝∠BAC， ∠EDC+∠DEC＝∠ACB，…………2分

∴∠BAD+∠DAC＝∠EDC+∠DEC．

∵DE＝DA，       …………3分

∴∠DAC＝∠DEC，   …………4分

∴∠BAD＝∠EDC． …………5分

（2）猜想：DM＝AM．理由如下：…………6分

∵点M、E关于直线BC对称，

∴∠MDC＝∠EDC，DE＝DM． …………7分

又由（1）知∠BAD＝∠EDC，

∴∠MDC＝∠BAD．

∵∠ADC＝∠BAD+∠B，

即∠ADM+∠MDC＝∠BAD+∠B，…………8分

∴∠ADM＝∠B＝60°．

又∵DA＝DE＝DM， 

∴△ADM是等边三角形，…………9分

∴DM＝AM．…………10分

23.（10分）证明（1）△BDF是等边三角形，…………1分

∵ED⊥AB，∠EDF＝30°，

∴∠FDB＝60°，            …………2分

∵∠A＝30°，∠ACB＝90°，

∴∠B＝60°，          …………3分

∴∠DFB＝60°，

∴△BDF是等边三角形． …………4分

（2）∵∠A＝30°，∠ACB＝90°，

∴AB＝2BC＝2， …………5分

∵△BDF是等边三角形，

∴BD＝BF＝2-a，…………6分

∴CF＝1﹣（2﹣a）

＝a-1  …………7分

（3）当EF∥AB时，∠CEF＝30°，∠FED＝∠EDA＝90°，

∴CF＝EF，EF＝DF，    …………8分

∵DF＝BF＝2-a，

∴a-1＝（2-a），   …………9分

∴a＝，

∴AD＝．     …………10分

24. （12分）（1）①   是．…………3分

∵∠ACB=90°，∠B=72°，

∴∠C=90°-72°=18°，

∵∠CPB=54°，

∴∠A+∠ACP=54°，

∴∠ACP=36°，

∴∠ACP=2∠A，

∴△ACP是“倍角三角形”，

故答案为：

②∵∠B=72°，△BPC是“倍角三角形”，

∴△BCP内角的度数分别是72°，72°，36°，…………4分

∴∠BCP=36°或72°，…………5分

∴∠ACP=54°或18°．…………7分

（2）满足条件的∠BCP的值为30°或40°或45°或50°或60°．………12分(一个1分)

如图2-1中，当△ABC是等腰直角三角形，CP⊥AB时，满足条件，此时∠BCP=45°．

如图2-2中，当∠A=60°，CP⊥AB时，满足条件，此时∠BCP=60°．

如图2-3中，当∠A=60°，∠BPC=100°时，满足条件，此时∠BCP=50°．

如图2-4中，当∠B=60°，∠APC=100°时，满足条件，此时∠BCP=40°．

如图2-5中，当∠B=60°，∠APC=90°时，满足条件，此时∠BCP=30°．

综上所述，满足条件的∠BCP的值为30°或40°或45°或50°或60°．

25.（14分）解：（1）（16﹣t）cm；…………3分

由题意可知AP＝t，BQ＝2t，

∵AB＝16cm，

∴BP＝AB﹣AP＝（16﹣t）cm，

（2）当点Q在边BC上运动，△PQB为等腰三角形时，则有BP＝BQ，…………4分

即16﹣t＝2t，解得t＝，…………6分

∴出发秒后，△PQB能形成等腰三角形；…………7分

（3）①当△BCQ是以BC为底边的等腰三角形时：CQ＝BQ，如图1所示，

则∠C＝∠CBQ，

∵∠ABC＝90°，

∴∠CBQ+∠ABQ＝90°．

∠A+∠C＝90°，

∴∠A＝∠ABQ，

∴BQ＝AQ，

∴CQ＝AQ＝10（cm），…………8分

∴BC+CQ＝22（cm），

∴t＝22÷2＝11；…………10分

②当，△BCQ是以BQ为底边的等腰三角形时：CQ＝BC，如图2所示，

则BC+CQ＝24（cm），

∴t＝24÷2＝12，…………13分

综上所述：当t为11或12时，△BCQ是以BC或BQ为底边的等腰三角形．……14分