人教A版 (2019)选择性必修 第二册5.1 导数的概念及其意义教案配套课件ppt

这是一份人教A版 (2019)选择性必修 第二册5.1 导数的概念及其意义教案配套课件ppt，共26页。PPT课件主要包含了学习目标，区间测速，车辆油耗，高台跳水，思考引入，平均速度，瞬时速度，重点内容，知识建构1，知识建构等内容，欢迎下载使用。
1.通过实例分析，经历由平均速度过渡到瞬时速度的过程.2.理解割线的斜率与切线的斜率之间的关系.3.体会极限思想.
三、抛物线的切线的斜率
问题1　在高台跳水中，运动员相对于水面的高度h与起跳后的时间存在函数关系h(t)＝－4.9t2＋4.8t＋11，根据上述探究，你能求该运动员在0≤t≤0.5,1≤t≤2 内的平均速度吗？
为了精准刻画运动员的运动状态，需要引入瞬时速度的概念. 我们把物体在某一时刻的速度称为瞬时速度. 那么，如何求运动员的瞬时速度呢？比如， 时的瞬时速度是多少？
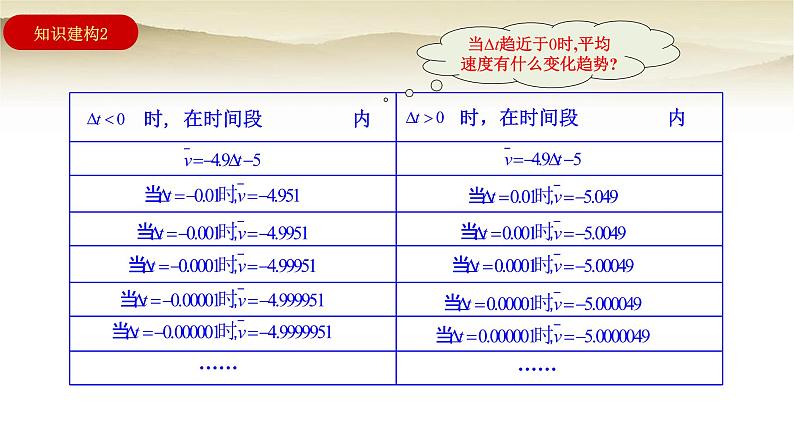
当Δt趋近于0时,平均速度有什么变化趋势?
我们发现，当 趋近于0时，即无论 t 从小于2的一边，还是从大于2的一边趋近于2时，平均速度都趋近于一个确定的值 . 从物理的角度看，时间间隔 无限变小时，平均速度 就无限趋近于 时的瞬时速度，因此，运动员在 时的瞬时速度是 .
1.瞬时速度：物体在　　　　的速度称为瞬时速度.2.瞬时速度的计算：设物体运动的时间与位移的函数关系式为y＝h(t)，则物体在t0时刻的瞬时速度为 　 .3.瞬时速度与平均速度的关系：从物理角度看，当时间间隔|Δt|无限趋近于0时，平均速度 就无限趋近于t＝t0时的瞬时速度.注意点：Δt可正，可负，但不能为0.
例1　某物体的运动路程s(单位：m)与时间t(单位：s)的关系可用函数s(t)＝t2＋t＋1表示，求物体在t＝1 s时的瞬时速度.
即物体在t＝1 s时的瞬时速度为3 m/s.
1.若本例中的条件不变，试求物体的初速度.
解　求物体的初速度，即求物体在t＝0时的瞬时速度，
即物体的初速度为1 m/s.
解　设物体在t0时刻的瞬时速度为9 m/s.
2.若本例中的条件不变，试问物体在哪一时刻的瞬时速度为9 m/s.
则2t0＋1＝9，∴t0＝4.则物体在4 s时的瞬时速度为9 m/s.
问题3　前面我们从物理的角度研究了瞬时速度的问题，它反映到我们几何上是什么意思？
割线位置 无限逼近 切线位置 割线斜率 无限逼近 切线斜率记点P的横坐标 x=1+Δx，则点P的坐标即为 (1+Δx,(1+Δx)2). 于是割线P0P 的斜率
从代数的角度列表展示上述过程： 让横坐标变化量 Δx趋近于0，割线斜率的趋近于2.
我们把”2”叫做“当Δx无限趋近于0时， 的极限“，记为 从几何图形上看，当横坐标间隔| Δx |无限变小时， 当点P无限趋近于点P0时，割线P0P无限趋近于点P0处的切线P0T 。割线P0P的斜率k 无限趋近于点P0处的切线的斜率k0. 因此，切线P0T 的斜率k0=2.
1.切线：设P0是曲线上一定点，P是曲线上的动点，当点P无限趋近于点P0时，割线P0P无限趋近于一个确定的位置，这个确定位置的直线P0T称为曲线在点P0处的切线.2.切线的斜率：设P0(x0，y0)是曲线y＝f(x)上一点，则曲线y＝f(x)在点P0(x0，y0)处的切线的斜率为k0＝ .
3.切线的斜率与割线的斜率的关系：从几何图形上看，当横坐标间隔|Δx|无限变小时，点P无限趋近于点P0，于是割线PP0无限趋近于点P0处的切线P0T，这时，割线PP0的斜率k无限趋近于点P0处的切线P0T的斜率k0.注意点：极限的几何意义：曲线y＝f(x)在x＝x0处的切线斜率.
P64页思考问题，小组完成回答问题
答 ： 前者的几何意义是过点（1，h(t)）、(1+Δt,h (1+Δt))的割线的斜率；后者是过点（1，h(t)）的切线的斜率。
例3　求抛物线f(x)＝x2－2x＋3在点(1,2)处的切线方程.
所以切线的方程为y－2＝0×(x－1)，即y＝2.
延伸探究　本例函数不变，求与2x－y＋4＝0平行的该曲线的切线方程.
故有2x0－2＝2，解得x0＝2，所以切点为(2,3)，所求切线方程为2x－y－1＝0.
(1)求抛物线在某点处的切线方程的步骤
(2)求曲线过某点的切线方程需注意，该点不一定是切点，需另设切点坐标.