数学八年级下册1.2 直角三角形的性质与判定（Ⅱ）第1课时教学设计

这是一份数学八年级下册1.2 直角三角形的性质与判定（Ⅱ）第1课时教学设计，共4页。教案主要包含了知识回顾，情境导入，探究学习，知识应用，巩固练习，课堂小结，作业，课外讨论等内容，欢迎下载使用。
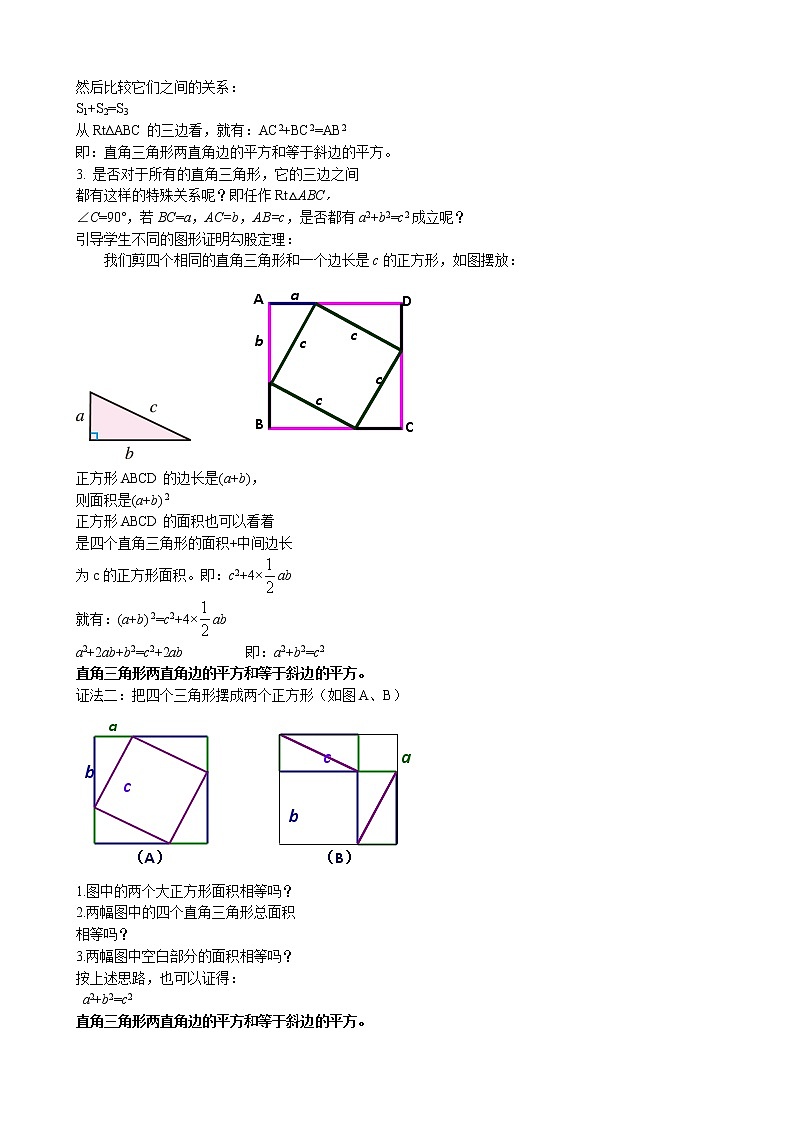
1.2 直角三角形的性质和判定（Ⅱ）第1课时教学目标1、让学生体验勾股定理的探索过程；掌握勾股定理；学会用勾股定理解决简单的几何问题．2、经历操作、归纳和猜想，用面积法推导作出肯定结论的过程，了解勾股定理3、了解我国古代数学家发现、推导和应用勾股定理中的贡献与成就，增进爱国主义情感，体验探索发现的过程和知识运用，增强学习数学的自信。重点：   勾股定理难点：   勾股定理的证明教学过程：一、知识回顾（出示ppt课件）1、三角形边的关系怎样？2、直角三角形是特殊的三角形，它有哪些特殊性质？在Rt △ABC，∠C=90°， ∠A=30°，点D是AB 的中点。3、直角三角形的三边有上述关系吗？直角三角形的三边是不是有特殊性质？二、情境导入（出示ppt课件）  向学生展示国际数学大会（ICM--2002）的会标图徽，并简要介绍其设计思路，从而激发学生勾股定理的兴趣。可以首次提出勾股定理。三、探究学习（出示ppt课件）1.在方格纸上画一个顶点都在格点上的直角三角形ABC，使两直角边分别为3cm和4cm，如图所示，试量出它的斜边c的长度.2.再分别以这个直角三角形的三边为为边长向外作正方形，得到三个大小不同的正方形，如图，那么这三个正方形的面积有什么关系呢？师生活动：在方格图中计算三个正方形的面积，然后比较它们之间的关系：S1+S2=S3从Rt∆ABC的三边看，就有：AC2+BC2=AB2即：直角三角形两直角边的平方和等于斜边的平方。3. 是否对于所有的直角三角形，它的三边之间都有这样的特殊关系呢？即任作Rt△ABC，∠C=90°，若BC=a，AC=b，AB=c，是否都有a2+b2=c2成立呢？ 引导学生不同的图形证明勾股定理：我们剪四个相同的直角三角形和一个边长是c的正方形，如图摆放：       正方形ABCD的边长是(a+b)，则面积是(a+b) 2正方形ABCD的面积也可以看着是四个直角三角形的面积+中间边长为c的正方形面积。即：c2+4×ab就有：(a+b) 2=c2+4×aba2+2ab+b2=c2+2ab         即：a2+b2=c2直角三角形两直角边的平方和等于斜边的平方。证法二：把四个三角形摆成两个正方形（如图A、B）          1.图中的两个大正方形面积相等吗？2.两幅图中的四个直角三角形总面积相等吗？3.两幅图中空白部分的面积相等吗？按上述思路，也可以证得： a2+b2=c2直角三角形两直角边的平方和等于斜边的平方。归纳定理：直角三角形的性质定理：（勾股定理）直角三角形两直角边a，b的平方和，等于斜边c的平方.   a2+ b2= c2.四、知识应用（出示ppt课件）例1、Rt∆ABC中，∠C=90°，AC=3，BC=4，求AB长。解：由勾股定理得：AC2+BC2=AB2AB=（已知两直角边求斜边，注意：分清直角边和斜边，已知哪条边，要求哪条边。）变式训练：Rt∆ABC中，∠A=90°，AC=3，BC=4，求AB长。（已知直角边和斜边，求另一条直角边）注意：（1）勾股定理只适用于直角三角形。（2）使用勾股定理时要明确哪个角是直角。例2、如图，在等腰三角形ABC中，AB=AC=13cm，BC=10cm.（1）你能算出BC边上的高AD的长吗？（2）△ABC的面积是多少呢？解：(1) 在Rt△ADC中，AD2=132-52=144. (勾股定理)所以AD=12. 所以AD的高为12cm.（2）因为三角形ACB中，面积=底×高÷2，即10×12÷2=60.所以 ABC的面积是60cm2.   五、巩固练习（出示ppt课件）   六、课堂小结（出示ppt课件）1、勾股定理：如果直角三角形的两直角边分别为a，b，斜边为c，那么：a2+b2=c22、能用几何语言描述。3、勾股定理的作用。注意的问题。    七、作业：P16   A      2、3、4     八、课外讨论（出示ppt课件）