


2022-2023 数学京改版新中考精讲精练 中考模拟卷(一)
展开中考模拟卷(一)
一、单选题
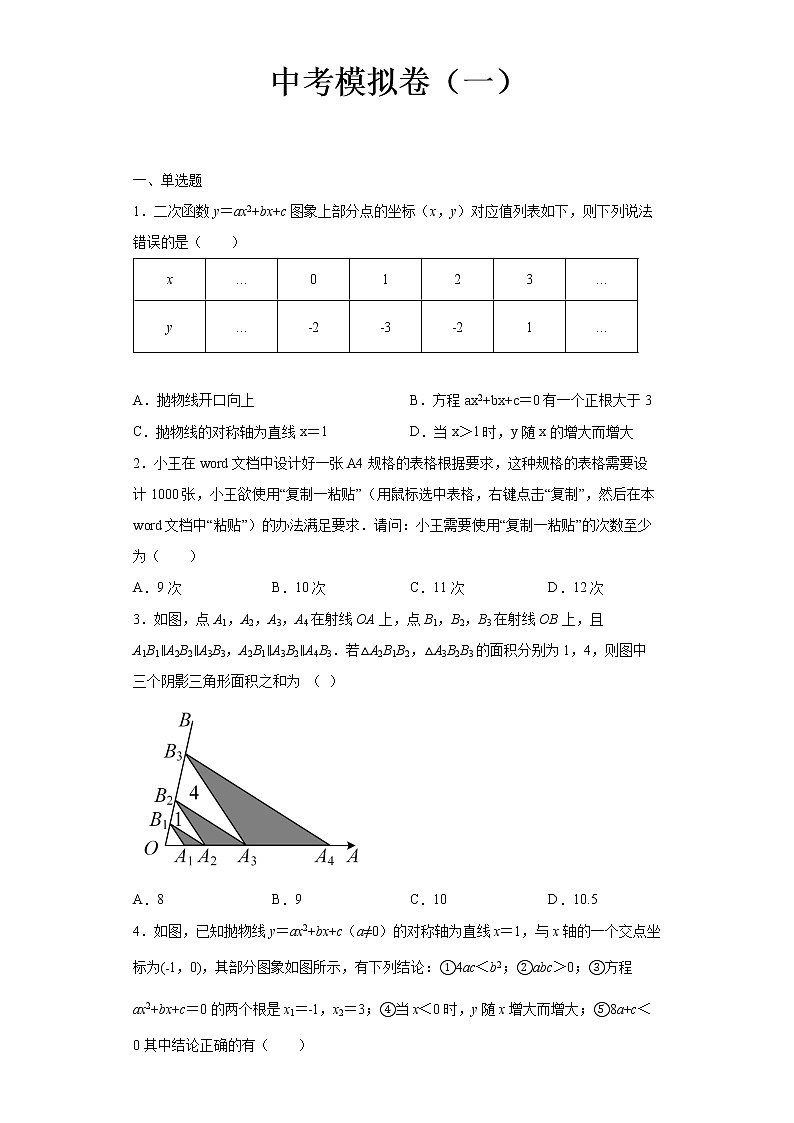
1.二次函数y=ax2+bx+c图象上部分点的坐标(x,y)对应值列表如下,则下列说法错误的是( )
x
…
0
1
2
3
…
y
…
﹣2
﹣3
﹣2
1
…
A.抛物线开口向上 B.方程ax2+bx+c=0有一个正根大于3
C.抛物线的对称轴为直线x=1 D.当x>1时,y随x的增大而增大
【答案】B
【分析】
首先根据表格中当和时,y都等于5,得出对称轴为,然后根据抛物线经过点(0,-2)得到抛物线开口向上,根据抛物线经过点(2,-2)和点(3,1)即可判断出方程ax2+bx+c=0根的情况,根据抛物线的开口方向和对称轴即可判断抛物线的增减性.
【详解】
解:∵二次函数经过点(0,-2)和点(2,-2),
∴二次函数的对称轴为,顶点坐标为(1,-3),
∴C选项正确;
∵抛物线与y轴交于点(0,-2),
∴抛物线开口向上,
∴A选项正确;
∵二次函数的对称轴为,经过点(2,-2)和点(3,1),
∴抛物线与x轴的正半轴交点的横坐标小于3,
∴方程ax2+bx+c=0有一个正根小于3,
∴B选项错误;
∵抛物线开口向上,对称轴为,
∴当x>1时,y随x的增大而增大,
∴D选项正确.
故选:B.
2.小王在word文档中设计好一张A4规格的表格根据要求,这种规格的表格需要设计1000张,小王欲使用“复制一粘贴”(用鼠标选中表格,右键点击“复制”,然后在本word文档中“粘贴”)的办法满足要求.请问:小王需要使用“复制一粘贴”的次数至少为( )
A.9次 B.10次 C.11次 D.12次
【答案】B
【分析】
根据题意得出第一次复制得2张,第二次复制最多得2×2=22=4张,第三次复制最多得2×2×2=23=8张,即可得出规律,第九次复制最多得29=512张,第十次复制最多得210=1024张,问题得解.
【详解】
解:由题意得第一次复制得2张,
第二次复制最多得2×2=22=4张,
第三次复制最多得2×2×2=23=8张,
第四次复制最多得2×2×2×2=24=16张,
……,
第九次复制最多得29=512张,
第十次复制最多得210=1024张,
1024>1000,
所以至少需要10次.
故选:B
3.如图,点A1,A2,A3,A4在射线OA上,点B1,B2,B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3.若△A2B1B2,△A3B2B3的面积分别为1,4,则图中三个阴影三角形面积之和为 ( )
A.8 B.9 C.10 D.10.5
【答案】D
【分析】
由题意得,,设A1B1,A2B2之间的距离为h,则由题意可得,再由可得,,从而得到问题的解答.
【详解】
∵A1B1∥A2B2
∴∠A1A2B1=∠A2A3B2
∵A2B1∥A3B2
∴∠A1A2B1=∠A2A3B2
∴ △A1A2B1∽△A2A3B2(AA)
同理可证△A2A3B2∽△A3A4B3,△A2B1B2∽△A3B2B3
∵△A2B1B2∽△A3B2B3,,
∴,
又∵△A1A2B1∽△A2A3B2
∴
设之间的距离为h,则:,
∴
又∵
∴
∴,
∵,△A1A2B1∽△A2A3B2
∴
∴,
同理有,
∴图中三个阴影三角形面积之和为:
,
故选:D.
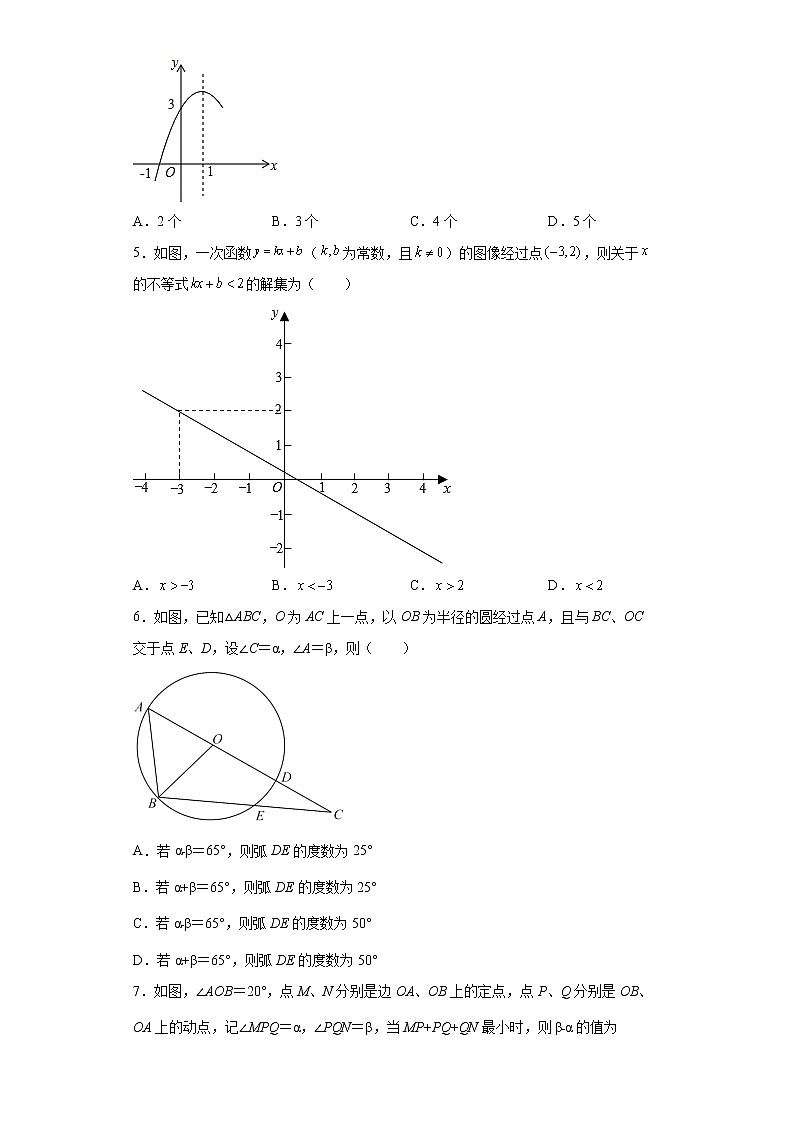
4.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,有下列结论:①4ac<b2;②abc>0;③方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;④当x<0时,y随x增大而增大;⑤8a+c<0其中结论正确的有( )
A.2个 B.3个 C.4个 D.5个
【答案】C
【分析】
由抛物线与x轴有2个交点即,可判断①;由抛物线开口向下,与y轴交于正半轴,而对称轴在y轴右侧,可判断a、b、c的正负即可判断②;由抛物线的对称轴为直线,点关于直线的对称点的坐标为即可判断③;由抛物线的对称轴为直线,可判断④;由对称轴,可得,图象可知,当时,,代入化简即可判断⑤.
【详解】
解:∵抛物线与x轴有2个交点,
∴,即,
∴①正确.
∵抛物线开口向下,与y轴交于正半轴,
∴,而对称轴在y轴右侧,
∴,而,
∴,因此,,
∴②错误.
∵抛物线的对称轴为直线,而点关于直线的对称点的坐标为,
∴方程的两个根是,
∴③正确.
∵抛物线的对称轴为直线,
∴当时,y随x增大而增大,
∴④正确.
∵,即,
观察图象可知,当时,,
∴,即,
∴⑤正确.
综上所述,①③④⑤正确,正确结论有4个,
故选C.
5.如图,一次函数(为常数,且)的图像经过点,则关于的不等式的解集为( )
A. B. C. D.
【答案】A
【分析】
根据图像的意义当x=-3时,kx+b=2,根据一次函数的性质求解即可.
【详解】
解:∵当x=-3时,kx+b=2,
且y随x的增大而减小,
∴不等式的解集,
故选A.
6.如图,已知△ABC,O为AC上一点,以OB为半径的圆经过点A,且与BC、OC交于点E、D,设∠C=α,∠A=β,则( )
A.若α﹣β=65°,则弧DE的度数为25°
B.若α+β=65°,则弧DE的度数为25°
C.若α﹣β=65°,则弧DE的度数为50°
D.若α+β=65°,则弧DE的度数为50°
【答案】D
【分析】
连接BD,根据圆周角定理求出∠ABD=90°,求出∠ADB=90°﹣β,再根据三角形外角性质得出90°﹣β=α+x,求出的度数是180°﹣2(α+β),再逐个判断即可.
【详解】
解答:解:连接BD,
设的度数是x,
则∠DBC=x,
∵AC过O,
∴∠ABD=90°,
∵∠A=β,
∴∠ADB=90°﹣β,
∵∠C=α,∠ADB=∠C+∠DBC,
∴90°﹣β=α+x,
解得:x=180°﹣2(α+β),
即的度数是180°﹣2(α+β),
当α﹣β=65°,即α=65°+β时,的度数是180°﹣2(65°+β+β)=50°﹣4β或180°﹣(α+α﹣65°)=245°﹣2α,故选项A,C不符合题意;
当α+β=65°时,的度数是180°﹣130°=50°,故选项B错误,选项D正确;
故选:D.
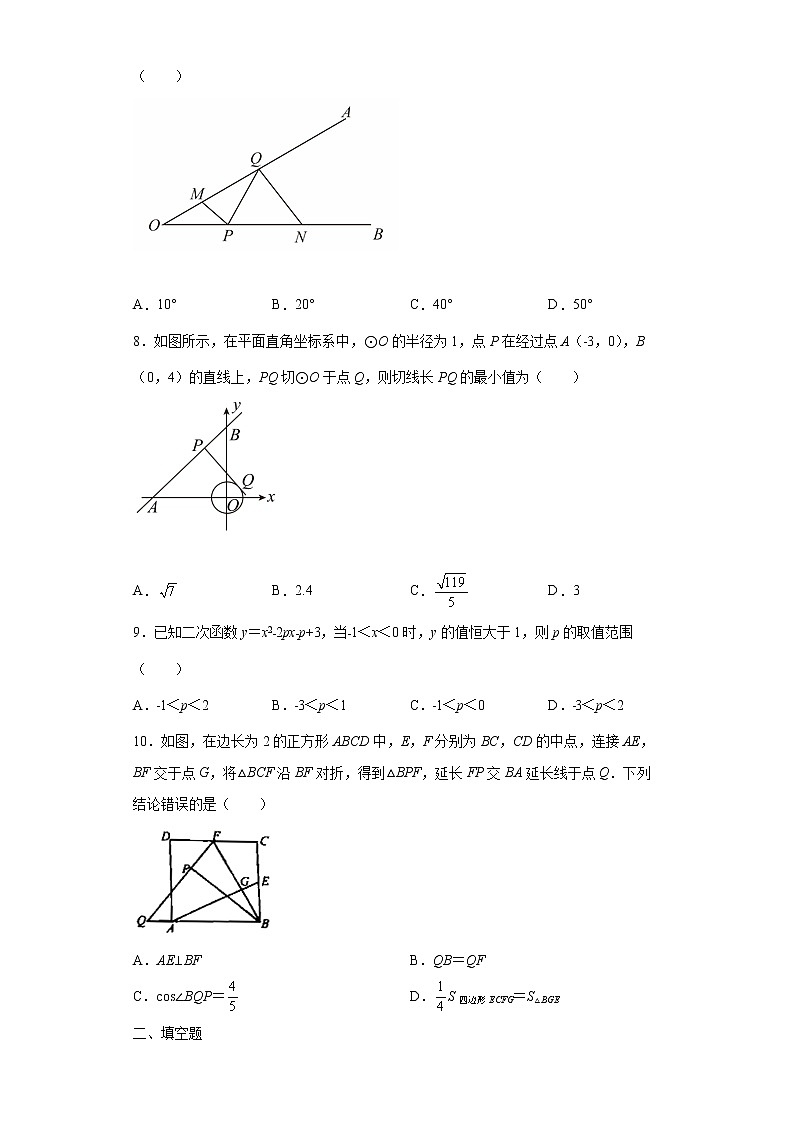
7.如图,∠AOB=20°,点M、N分别是边OA、OB上的定点,点P、Q分别是OB、OA上的动点,记∠MPQ=α,∠PQN=β,当MP+PQ+QN最小时,则β﹣α的值为( )
A.10° B.20° C.40° D.50°
【答案】C
【分析】
作M关于OB的对称点,N关于OA的对称点,连接交OA于Q,交OB于P,则MP+PQ+QN最小易知∠OPM=∠OP=∠NPQ,∠OQP=∠AQ=∠AQN,根据三角形的外角的性质和平角的定义即可得到结论.
【详解】
解:如图,作M关于OB的对称点,N关于OA的对称点,连接交OA于Q,交OB于P,则MP+PQ+QN最小,
∴∠OPM=∠OP=∠NPQ,∠OQP=∠AQ=∠AQN,
∴∠QPN=(180°−α)=∠AOB+∠MQP=20°+(180°−β),
∴180°−α=40°+(180°−β),
∴β−α=40°,
故选:C.
8.如图所示,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(﹣3,0),B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
A. B.2.4 C. D.3
【答案】C
【分析】
由切线的性质可知,线段PQ、OP、OQ组成直角三角形,其中OQ为半径,是个定值,勾股定理可知,当切线PQ最短时,必有OP最短,由此当时,此时切线长PQ有最小值,通过三角形等面积法求出PQ,再利用勾股定理求出PQ.
【详解】
解:如图所示:连接OP、OQ,
PQ切⊙O于点Q,
,为直角三角形,
由勾股定理可知:,
故当OP有最小值时,PQ也有最小值,
根据点到直线距离,垂线段最短可知:当,OP有最小值,
如下图所示:过点O向AB作垂线,垂足为P,并在圆上找到对应切点Q,连接PQ与OQ.
点A(﹣3,0),B(0,4),
,,
在中,由勾股定理可得:,
利用等面积法可得: 解得:
故,
故选:C.
9.已知二次函数y=x2﹣2px﹣p+3,当﹣1<x<0时,y的值恒大于1,则p的取值范围( )
A.﹣1<p<2 B.﹣3<p<1 C.﹣1<p<0 D.﹣3<p<2
【答案】D
【分析】
将x=-1代入函数的解析式,令y>1即可求得p的取值范围.
【详解】
解:二次函数 的图象是一条开口向上的抛物线,
(1)当抛物线的对称轴x= p≤-1时,只要使二次函数解析式的值-1 < x < 0时恒大于1,所以x= -1,y=1 +2p-p+3=p+4> 1,解得: p> -3;
(2) 当抛物线的对称轴x= p≥0时,只要使二次函数解析式的值-1 < x < 0时恒大于1,所以x=0,y=-p+3> 1,所以要使二次函数解析式的值 -1 < x < 0时恒大于1,只要p < 2即可;
(3) 当抛物线的对称轴x= p在区间-1 < x < 0时,
此时,-2< p< 1.
综上所述:p的取值范围是:-3
10.如图,在边长为2的正方形ABCD中,E,F分别为BC,CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q.下列结论错误的是( )
A.AE⊥BF B.QB=QF
C.cos∠BQP= D.S四边形ECFG=S△BGE
【答案】C
【分析】
△BCF沿BF对折,得到△BPF,利用角的关系求出QF=QB,即可判断B;首先证明△ABE≌△BCF,再利用角的关系求得∠BGE=90°,即可得到AE⊥BF即可判断A;利用QF=QB,解出BP,QB,根据正弦的定义即可求解即可判断C;可证△BGE与△BCF相似,进一步得到相似比,再根据相似三角形的性质即可求解即可判断D.
【详解】
解:∵四边形ABCD是正方形,
∴∠C=90°,AB∥CD,
由折叠的性质得:FP=FC,∠PFB=∠BFC,∠FPB=∠C=90°,
∵CD∥AB,
∴∠CFB=∠ABF,
∴∠ABF=∠PFB,
∴QF=QB,故B选项不符合题意;
②∵E,F分别是正方形ABCD边BC,CD的中点,
∴CD=BC,,,∠ABE=∠C=90°,
∴CF=BE,
在△ABE和△BCF中,
,
∴△ABE≌△BCF(SAS),
∴∠BAE=∠CBF,
又∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴∠BGE=90°,
∴AE⊥BF,故A选项不符合题意;
令PF=k(k>0),则PB=2k,
在Rt△BPQ中,设QB=x,
∵,
∴x2=(x﹣k)2+4k2,
∴x=,
∴cos∠BQP=,故C选项符合题意;
⑤∵∠BGE=∠BCF,∠GBE=∠CBF,
∴△BGE∽△BCF,
∵BE=BC,BF=BC,
∴BE:BF=1:,
∴△BGE的面积:△BCF的面积=1:5,
∴S四边形ECFG=4S△BGE,故D选项不符合题意.
故选C.
二、填空题
11.现有5张除数字外完全相同的卡片,上面分别写有,,0,1,2这五个数,将卡片背面朝上洗匀,从中任意抽取两张,将卡片上的数字记为.
(1)用列表法或画树状图法列举的所有可能结果.
(2)若将m,n的值代入二次函数,求二次函数顶点在坐标轴上的概率.
【答案】(1)见解析;(2).
【分析】
(1)画出树状图即可;
(2)共有20种可能的结果,其中二次函数顶点在坐标轴上的结果有8种,再由概率公式求解即可.
【详解】
(1)画树状图得
共有20种可能的结果;
(2)从,,0,1,2这五个数中任取两数m,n,共有20种可能,
其中二次函数顶点在坐标轴上(记为事件A)的有8种,
所以.
12.若2<x<5,则|x﹣2|﹣|5﹣x|=_______.
【答案】2x-7
【分析】
根据2<x<5,得到x-2>0,5-x<0,根据绝对值的意义去绝对值,去括号,合并同类项即可求解.
【详解】
解:因为2<x<5,
所以x-2>0,5-x<0,
所以|x﹣2|﹣|5﹣x|
=(x-2)-(5-x)
=x-2-5+x
=2x-7.
故答案为:2x-7
13.将抛物线y=x22x+2向上左移一个单位后,那么新的抛物线的表达式是______.
【答案】
【分析】
根据函数图像的平移方法,左加右减,上加下减判断即可;
【详解】
抛物线y=x22x+2向上左移一个单位后得:
;
故答案是:.
14.已知Rt△ABC中,∠ACB=90°,CD⊥AB于D,∠BCD=2∠B,AC=4,则BD的长为________.
【答案】6
【分析】
由∠BCD=2∠B,可得∠B=∠ACD=30゜,则由含30度直角三角形的性质可求得AD与AB的长,从而其差即是BD的长.
【详解】
∵CD⊥AB
∴∠B+∠BCD=90゜
∵∠BCD=2∠B
∴∠B+2∠B=90゜
∴∠B=30゜
∴∠BCD=60゜,AB=2AC=8
∵∠ACB=90°
∴∠ACD=30゜
∴
∴
故答案为;6
15.已知:am=2,an=3,则a2m+n=________.
【答案】12
【分析】
根据同底数幂的乘法和幂乘方的逆运算把原式化简,再把am=2,an=3代入即可.
【详解】
解:∵am=2,an=3,
∴,
故答案为:12.
16.如图,在Rt△ABC中,∠C=90°,BC=2,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为____或___
【答案】3;
【分析】
分两种情况讨论:①当B′D⊥AE时,△AB′F为直角三角形;②当DB′⊥AB′时,△AB′F为直角三角形.
【详解】
解:①当B′D⊥AE时,△AB′F为直角三角形,如下图:
根据题意,BE=B′E,BD=B′D=BC=,∠B=∠EB′F,
∵在Rt△ABC中,∠C=90°,BC=2,AC=2,
∴AB===4,
∴,
∴∠B=∠EB′F =30°,
∵在Rt△BDF中,∠B=30°,
∴DF=BD=,
∴B′F=B′D-DF=-=,
∵在Rt△B′EF中,∠EB′F =30°,
∴EF=B′E,
∵B′F===EF,
即=EF,
∴EF=,则BE=1,
∴AE=AB-BE=4-1=3.
②当DB′⊥AB′时,△AB′F为直角三角形,如下图:
连接AD,过A作AN⊥EB′,交EB′的延长线于N,
根据题意,BE=B′E,BD=CD=B′D=BC=,∠DBE=∠EB′F,
∵在Rt△ABC中,∠C=90°,BC=2,AC=2,
∴AB===4,
∴,
∴∠DBE=∠EB′F =30°,
∵∠AB′F=90°,
∴∠AB′E=∠AB′F+∠EB′F=120°,
∴Rt△AB′N中,∠AB′N=60°,∠B′AN=30°,
∴B′N=AB′,
在Rt△AB′D和Rt△ACD中
,
∴Rt△AB′D≌Rt△ACD(HL),
∴AB′=AC=2,
∴B′N=1,AN=,
设AE=x,则BE= B′E=4-x,
∵在Rt△AEN中,,
∴()2+(4-x+1)2=x2
∴x=
综上,AE的长为3或,
故答案为:3或.
17.x、y表示两个数,规定新运算“*”如下:x*y=2x﹣3y,那么(3*5)*(﹣4)=_____.
【答案】-6
【分析】
根据找出新的运算方法,再根据新的运算方法计算即可.
【详解】
故答案为:
三、解答题
18.列方程解应用题:在生产操作中,有些化工原料对人体有害,所以需要用机器人来搬运. 现有 A、B两种机器人,A型机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg所用时间与B型机器人搬运600kg所用时间相等,则两种机器人每小时分别搬运多少化工原料?
【答案】A型机器人每小时搬运90kg化工原料,B型机器人每小时搬运60kg化工原料
【分析】
设A型机器人每小时搬运化工原料,则B型机器人每小时搬运化工原料,然后根据A型机器人搬运900kg所用时间与B型机器人搬运600kg所用时间相等列出方程求解即可.
【详解】
解:设A型机器人每小时搬运化工原料,则B型机器人每小时搬运化工原料,
由题意得:
解得:
经检验,是原方程的根.
故该方程的解为,.
答:A型机器人每小时搬运90kg化工原料,B型机器人每小时搬运60kg化工原料.
19.(1)计算:
(2)计算:
(3)先化简,再求值:,其中x=3,y=﹣1.
【答案】(1);(2);(3),
【分析】
(1)利用完全平方公式和平方差公式进行求解即可;
(2)利用完全平方公式和多项式乘以多项式的计算法则求解即可;
(3)根据分式的混合计算法则先化简,然后代值计算即可.
【详解】
解:(1)
;
(2)
;
(3)
,
当,时,原式.
20.(1)将二次函数化成的形式,并指出开口方向、顶点坐标和对称轴
(2)已知某抛物线的顶点坐标是(3,—5),且经过点A(1,3).求此抛物线的解析式;
(3)已知某抛物线经过三点,求此抛物线的解析式
【答案】(1),开口向下,顶点坐标为(1,),对称轴为直线.(2)抛物线解析式为.(3)抛物线解析式为.
【分析】
(1)利用配方法将二次函数化成的形式,通过观察化成后的顶点式,确定开口方向、顶点坐标和对称轴.
(2)直接设顶点式,把顶点代入顶点式中,最后通过A(1,3),求出值,最后便得到答案.
(3)为交点坐标,故设交点式:,代入交点坐标,最后通过求出值,最后便得到答案.
【详解】
(1)解:
由顶点式可知:顶点坐标为(1,),对称轴为直线,
由于,开口方向向下.
(2)解:(3,—5)是该抛物线顶点坐标,
由顶点式可知,该抛物线为:,
抛物线经过点A(1,3),
解得:,
抛物线解析式为:.
(3)解: 为抛物线与轴的交点坐标,
由交点式可知,该抛物线为:,
抛物线经过点,
解得:,
抛物线解析式:.
21.已知A(1,1),B(﹣3,﹣1),C(﹣3,1),是平面直角坐标系中的3个点,
(1)画出△ABC的外接圆⊙P,⊙P的圆心坐标为______;
(2)若在x轴上负半轴有一点F,且∠AFB=∠ACB,则点F的坐标为 .
【答案】(1);(2)
【分析】
(1)根据三点确定圆心,找到的垂直平分线的交点,即为所求;
(2)根据点的坐标,证明是,则,即是直径,勾股定理求得,则=,进而求得点的坐标
【详解】
解:(1)根据三点确定圆心,找到的垂直平分线的交点,即为所求,如图所示;
故答案为:
(2),
是,则,即是直径,
在x轴上负半轴有一点F,∠AFB=∠ACB,
故答案为:
22.一块直角三角形木板,一直角边BC长75 cm,另一直角边AC长 100 cm,要把它加工成面积最大的正方形棋盘,小明、小亮二人的加工方法分别如图1、图2所示,请运用所学知识说明谁的加工方法得到的正方形面积较大.
【答案】小亮的加工的方法获得的正方形面积较大.
【分析】
根据题意分别求得小明、小亮二人的加工的正方形的边长,设小明加工的正方形棋盘的边长为,小亮加工的正方形棋盘的边长为.如图1,过点作,垂足是点,与相交于点.证明,根据等面积法即可求得,进而求得的边长,图2中证明,即可求得的边长,进而比较大小即可.
【详解】
解:设小明加工的正方形棋盘的边长为,小亮加工的正方形棋盘的边长为.如图1,过点作,垂足是点,与相交于点.
,
.
,即.
,
.
又,
.解得.
,解得.
如图2,,
.
,即.
解得.
,
∴故小亮的加工的方法获得的正方形面积较大.
23.在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成的矩形的周长与面积相等,则称这个点为“美好点”,如图,过点P分别作x轴,y轴的垂线,与坐标轴围成的矩形OAPB的周长与面积相等,则P为“美好点”.
(1)在点M(2,2),N(4,4),Q(﹣6,3)中,是“美好点”的有 ;
(2)若“美好点”P(a,﹣3)在直线y=x+b(b为常数)上,求a和b的值;
(3)若“美好点”P恰好在抛物线第一象限的图象上,在x轴上是否存在一点Q使得△POQ为直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
【答案】(1)N、Q;(2)a=6,b=﹣9或a=﹣6,b=3;(3)存在,点Q的坐标为(6,0)或(,0).
【分析】
(1)根据“美好点”的定义逐个验证即可;
(2)对于P点,对应图形的周长为:2×(|a|+3)=2|a|+6,面积为3|a|,因为点P是“美好点”,故2|a|+6=3|a|,即可求解;
(3)根据点P是“美好点”确定点P的坐标,设点Q的坐标为(x,0),再分以下三种情况:当∠POQ=90°时,此种情况不存在;当∠PQO=90°时,则PO2=PQ2+OQ2;当∠OPQ=90°时,则OQ2=PQ2+OP2,分别列出关于x的方程,解得x即可.
【详解】
解:(1)对于M点,对应图形的周长为:2×(2+2)=8,面积为2×2=4≠8,故点M不是“美好点”;
对于点N,对应图形的周长为:2×(4+4)=16,面积为4×4=16,故点N是“美好点”;
对于点Q,对应图形的周长为:2×(6+3)=18,面积为6×3=18,故点Q是“美好点”;
故答案为:N、Q;
(2)对于P点,对应图形的周长为2×(|a|+3)=2|a|+6,面积为3|a|,
∵点P是“美好点”,
∴2|a|+6=3|a|,解得:a=±6,
将P(a,﹣3)代入y=x+b得:﹣3=a+b,则b=﹣3﹣a,
∴当a=6时,b=-9;当a=-6时,b=3,
故a=6,b=﹣9或a=﹣6,b=3;
(3)存在,理由如下:
设点P的坐标为(m,n),则n=m2(m>0,n>0),
由题意得:2m+2n=mn,∴2m+m2=m3,
解得:m=6或﹣4(舍去)或0(舍去),
故点P的坐标为(6,3);
设点Q的坐标为(x,0),
则PQ2=(x﹣6)2+32=(x﹣6)2+9,
PO2=36+9=45,
OQ2=x2,
当∠POQ=90°时,∵点Q在x轴上,则∠POQ≠90°,此种情况不存在;
当∠PQO=90°时,则PO2=PQ2+OQ2,∴45=(x﹣6)2+9+ x2,解得x=6或x=0(舍去);
当∠OPQ=90°时,则OQ2=PQ2+OP2,∴x2=(x﹣6)2+9+45,解得x=;
综上所述,符合条件的点Q的坐标为:(6,0)或(,0).
24.通过实验研究发现:初中生在体育课上运动能力指标(后简称指标)随上课时间的变化而变化.上课开始时,学生随着运动,指标开始增加,中间一段时间,指标保持平稳状态,随后随着体力的消耗,指标开始下降.指标y随时间x(分钟)变化的函数图象如图所示,当和时,图象是线段;当时,图象是反比例函数的一部分.
(1)求这个分段函数的表达式;
(2)杨老师想在一节课上进行某项运动的教学需要18分钟,这项运动需要学生的运动能力指标不低于48才能达到较好的效果,他的教学设计能实现吗?请说明理由.
【答案】(1)0-10分钟的函数解析式为,20-40分钟的函数解析式为;(2)杨老师的教学设计能实现,理由见解析
【分析】
(1)设0-10分钟的函数解析式为,20-40分钟的函数解析式为,然后利用待定系数法求解即可;
(2)将代入中得,代入中得,由此求解即可.
【详解】
解:(1)设0-10分钟的函数解析式为,20-40分钟的函数解析式为,
∴,,
∴,,
∴0-10分钟的函数解析式为,20-40分钟的函数解析式为;
(2)将代入中得,
将代入中得,
∵,
∴杨老师的教学设计能实现.
25.如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD,AC分别交于点E,F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若BC=2AB,BC=4,求⊙O的半径.
【答案】(1)直线CE与⊙O相切,理由见解析;(2)
【分析】
(1)连接OE,则OA=OE,可得∠OAE=∠OEA,根据矩形性质和平行线性质可得∠OAE=∠ACB,则∠DCE=∠OEA,由∠D=90°可证得∠DEC+∠OEA=90°即∠OEC=90°,根据切线的判定即可做出判断;
(2)连接EF,则∠AEF=90°,由tan∠ACB=tan∠EAF=tan∠DCE可求得DE、AE、EF,再根据勾股定理求得AF即可解答.
【详解】
解:(1)直线CE与⊙O相切,理由为:
连接OE,则OA=OE,
∴∠OAE=∠OEA,
∵四边形ABCD是矩形,
∴BC∥AD,∠D=90°,
∴∠OAE=∠ACB,
∵∠ACB=∠DCE.
∴∠OAE=∠DCE.
∴∠DCE=∠OEA,
∵∠D=90°,
∴∠DEC+∠DCE=90°,
∴∠DEC+∠OEA=90°即∠OEC=90°,
∵OE是半径,
∴直线CE与⊙O相切;
(2)∵BC=2AB,BC=4,
∴AB=2,
∵四边形ABCD是矩形,
∴∠B=∠D=90°,AD=BC=4,CD=AB=2,
连接EF,
∵AF是⊙O的直径
∴∠AEF=90°,
∵∠B=∠D=90°,∠ACB=∠DCE=∠FAE,
∴tan∠ACB =tan∠DCE=tan∠EAF,
∴即,
解得:DE=1,EF=,AE=4-DE=3,
在Rt△AEF中,,
∴OA=即⊙O的半径.
2022-2023 数学京改版新中考精讲精练 中考模拟卷(三): 这是一份2022-2023 数学京改版新中考精讲精练 中考模拟卷(三),文件包含2022-2023数学京改版新中考精讲精练中考模拟卷三解析版docx、2022-2023数学京改版新中考精讲精练中考模拟卷三原卷版docx等2份试卷配套教学资源,其中试卷共77页, 欢迎下载使用。
2022-2023 数学京改版新中考精讲精练 中考模拟卷(二): 这是一份2022-2023 数学京改版新中考精讲精练 中考模拟卷(二),文件包含2022-2023数学京改版新中考精讲精练中考模拟卷二解析版docx、2022-2023数学京改版新中考精讲精练中考模拟卷二原卷版docx等2份试卷配套教学资源,其中试卷共55页, 欢迎下载使用。
2022-2023 数学京改版新中考精讲精练 考点30概率及有关计算: 这是一份2022-2023 数学京改版新中考精讲精练 考点30概率及有关计算,文件包含2022-2023数学京改版新中考精讲精练考点30概率及有关计算解析版docx、2022-2023数学京改版新中考精讲精练考点30概率及有关计算原卷版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。












