2023届河南省顶级名校高三上学期10月阶段性测试数学（理）试题（解析版）

2023届河南省顶级名校高三上学期10月阶段性测试数学（理）试题

一、单选题

1．已知集合，则集合的子集个数为（    ）

A．0 B．1 C．2 D．4

【答案】C

【解析】求出，根据元素个数，即可求解.

【详解】

，

子集有和.

故选:C

【点睛】本题考查交集的运算以及子集关系，属于基础题.

2．复数(为虚数单位)的模是

A． B． C．1 D．2

【答案】B

【分析】先求出复数的最简形式，再利用复数的模的公式求解即可．

【详解】因为，所以，选B．

【点睛】本题主要考查复数的运算及复数的模，属基础题．

3．在一个正方体中，过顶点A的三条棱的中点分别为E，F，G．该正方体截去三棱锥后，所得多面体的三视图中，正视图如图所示，则相应的侧视图是（ ）

A． B． C． D．

【答案】D

【分析】根据题意及题目所给的正视图还原出几何体的直观图，结合直观图进行判断.

【详解】由题意及正视图可得几何体的直观图，如图所示，

所以其侧视图为

故选：D

4．《中国共产党党旗党徽制作和使用的若干规定》指出，中国共产党党旗为旗面缀有金黄色党徽图案的红旗，通用规格有五种.这五种规格党旗的长(单位:cm)成等差数列，对应的宽为(单位: cm),且长与宽之比都相等，已知，，，则

A．64 B．96 C．128 D．160

【答案】C

【分析】设等差数列公差为，求得，得到，结合党旗长与宽之比都相等和，列出方程，即可求解.

【详解】由题意，五种规格党旗的长(单位:cm)成等差数列，设公差为，

因为，，可得，

可得，

又由长与宽之比都相等，且，可得，所以.

故选：C.

5．已知，，，则与的夹角为

A． B． C． D．

【答案】D

【分析】根据公式，，，已知，代入，即可解得，进而求出夹角．

【详解】，由题得，则.故选D.

【点睛】本题考查数量积的定义，由公式即可直接求出两个向量的夹角，属于基础题．

6．（1+2x2 ）（1+x）4的展开式中x3的系数为

A．12 B．16 C．20 D．24

【答案】A

【分析】本题利用二项展开式通项公式求展开式指定项的系数．

【详解】由题意得x3的系数为，故选A．

【点睛】本题主要考查二项式定理，利用展开式通项公式求展开式指定项的系数．

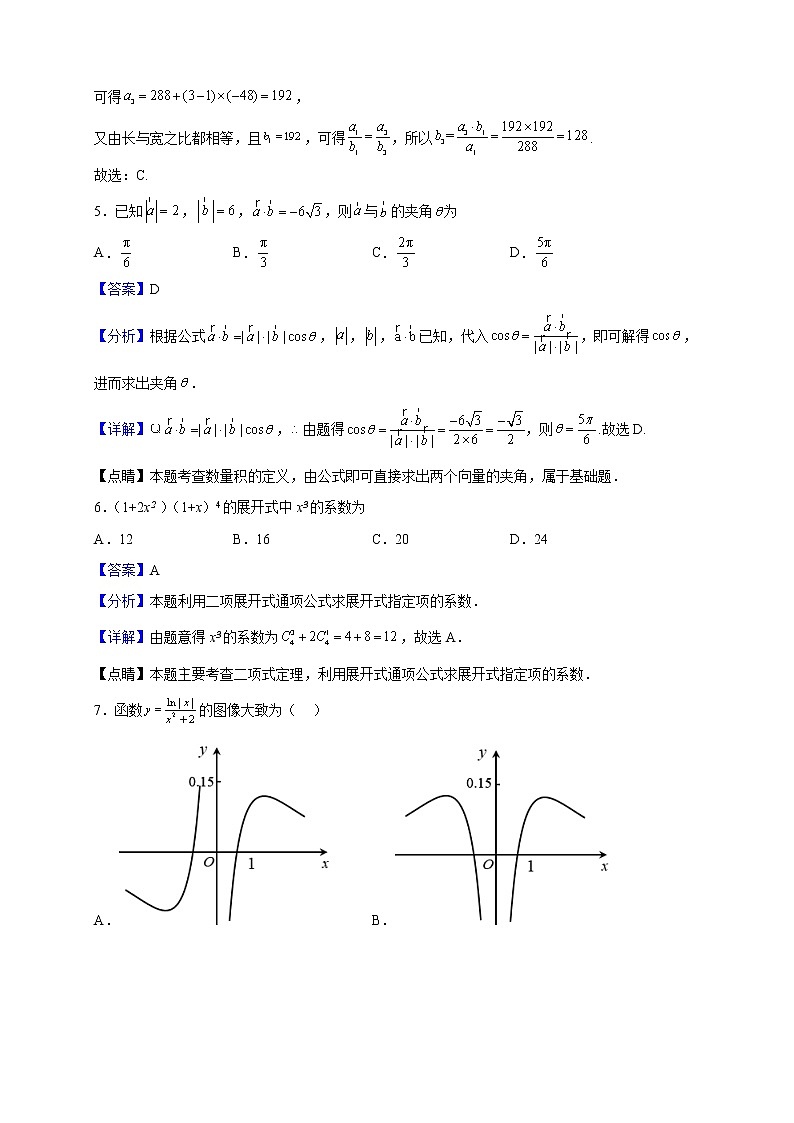
7．函数的图像大致为（    ）

A． B．

C． D．

【答案】B

【分析】由函数为偶函数可排除AC，再由当时，，排除D，即可得解.

【详解】设，则函数的定义域为，关于原点对称，

又，所以函数为偶函数，排除AC；

当时， ，所以，排除D.

故选：B.

8．已知偶函数的定义域为，且当时，则曲线在点处的切线斜率为

A． B． C． D．

【答案】C

【解析】根据偶函数的对称性可知，根据解析式求得，进而得到所求结果.

【详解】由题意得，偶函数的图象关于轴对称    

当时，    ，则

本题正确选项：

【点睛】本题考查函数奇偶性和对称性、导数的几何意义的应用，关键是能够通过函数的对称性得到导数值之间的关系.

9．函数在定义域内单调且对任意时，都有 ，，若正实数a，b，c互不相等，且，则的取值范围为（    ）

A． B． C． D．

【答案】A

【分析】由已知，，作出函数图象，根据图象，可知，当时，有3个交点，根据函数解出a，b，c关系，表示出即可.

【详解】因为，函数在定义域内单调

且对任意时，都有

所以，设，则有，，，，

即，.

又，         所以，，解得.

则，所以

由题意值，若a，b，c互不相等，且，

如图，不妨a<b<c，由已知条件可知：，

且，则.

又，则，所以，

因为，           所以，

所以，

故选：A.

10．设函数，已知在有且仅有5个零点，下述四个结论中，正确结论的编号是（    ）

①在有且仅有3个极大值点

②在有且仅有2个极小值点

③在单调递增              

④的取值范围是

A．①④ B．②③ C．①②③ D．①③④

【答案】A

【分析】本题为三角函数与零点结合问题，难度大，通过整体换元得，结合正弦函数得图象分析得出答案.

【详解】当时，，

在有且仅有5个零点，

，

，故④正确；

由，知时，

令时取得极大值，①正确；

极小值点不确定，可能是2个也可能是3个，②不正确；

因此由选项可知只需判断③是否正确即可得到答案，

当时，，

若在单调递增，

则 ，即 ，

，故③不正确．

故选：A.

11．设函数的定义域为，且满足是偶函数，，当时，，则下列说法不正确的是（       ）

A．

B．当时，的取值范围为

C．为奇函数

D．方程仅有5个不同实数解

【答案】D

【分析】根据函数的周期性，奇偶性，指定区间上的函数图象，数形结合的思想结合即可.

【详解】依题意， 是偶函数，图像关于 对称，又，即，因此有，即，于是有，从而得函数的周期，

对于A，，故A正确；

对于B，如图，故B正确；

对于C，，函数为奇函数，故C正确；

对于D，在同一坐标平面内作出函数、的部分图象，如图，方程的实根，仅有6个不同实数解，故D错误.

故选：D.

12．已知点为抛物线的焦点，，点为抛物线上一动点，当最小时，点恰好在以，为焦点的双曲线上，则该双曲线的离心率为（    ）

A． B． C． D．

【答案】C

【分析】过点作垂直于抛物线的准线于点B，进而根据抛物线的定义得取得最大值时，取得最小值，此时与抛物线相切，再根据直线为抛物线的位置关系得，再结合双曲线的定义求解即可.

【详解】由抛物线的对称性，设为抛物线第一象限内点，如图所示：

过点作垂直于抛物线的准线于点B，

由抛物线的定义知，

因为轴，可得，

，

当取得最大值时，取得最小值，此时与抛物线相切，

此时，设的直线方程为，

联立，整理得，

其中，解得：，

由为抛物线第一象限内点，则.

所以，，解得：，此时，即或.

所以点的坐标为.

由题意知，双曲线的左焦点为，右焦点为.

设双曲线的实轴长为，则，

所以，，又，

所以，.

故选：C

二、填空题

13．已知实数，满足约束条件则的最小值为___________.

【答案】

【分析】先作出不等式组表示的平面区域，再结合目标函数所对应的直线，观察直线所在的位置求目标函数的最小值即可.

【详解】解：由实数，满足约束条件，作出可行域如图所示，联立，解得，由简单的线性规划问题可得，当目标函数所对应的直线过点时，目标函数取最小值，即当时，目标函数取最小值，

故答案为.

【点睛】本题考查了简单的线性规划问题，重点考查了数形结合的数学思想方法，属中档题.

14．“关注夕阳、爱老敬老”—某马拉松协会从2013年开始每年向敬老院捐赠物资和现金.下表记录了第年（2013年是第一年）与捐赠的现金（万元）的对应数据，由此表中的数据得到了关于的线性回归方程，则预测2019年捐赠的现金大约是______万元.

【答案】5.25

【分析】首先根据数据求样本中心点，代入求，当时，求2019年捐赠的现金.

【详解】由已知得样本点的中心点的坐标为，代入，

得，即，所以，取，

得，预测2019年捐赠的现金大约是5.25万元.

故答案为：5.25

【点睛】本题考查回归直线方程的求解和应用，属于基础题型.

15．已知是等比数列，公比大于1，且，．记为在区间中的项的个数，则数列的前30项的和的值为______．

【答案】

【分析】由题知，，，，，，，再根据题意求解的前30项，并求和即可.

【详解】解：设等比数列的公比为，因为是等比数列，，，

所以，，解得，或，（舍去），

所以，，，，，，，，

所以对应区间为， 则；

，对应的区间分别为，，都只有一项，则；

，，，对应的区间分别为，，，，都只有，两项，则；

，，，，，，，对应的区间分别为，，，，，，，，

都只有，，三项，即；

，，…对应的区间分别为，，…，，都只有，，，四项，；

所以．

故答案为：

16．已知，其中为自然对数的底数，则由大到小依次为______.

【答案】

【分析】构造函数，，，由单调性得出.

【详解】令，，

令，，

当时，，单调递增，又，所以

又，所以，在成立，所以，令，，在为减函数，所以

即，令，，在为减函数

所以，即，所以，成立

令，则上式变为 所以.

所以，所以.

故答案为：

【点睛】关键点睛：在比较大小时，有时可以构造函数，利用导数得出其单调性，进而得出大小关系.

三、解答题

17．已知的内角A，B，C的对边分别为a，b，c，且.

(1)求角B的大小；

(2)若BC边上的高为，求.

【答案】(1)

(2)

【分析】（1）先根据式子形式采取角化边，然后利用余弦定理的推论即可解出；

（2）先根据锐角三角函数的定义可知，，得出关系，再根据可求出，然后根据三角形内角和定理，诱导公式，两角和的正弦公式化简，即可解出．

【详解】（1）由，得，即，∴，∵，∴.

（2）∵，且BC边上的高为，∴，∴，

∴.∵，∴C为锐角，∴，

∴.

18．如图， 三棱柱中，侧面，已知，，，点是棱的中点

(1)求证：平面：

(2)求二面角的余弦值；

【答案】(1)证明见解析

(2)

【分析】（1）作出辅助线，利用余弦定理求出，利用勾股定理逆定理得到，进而证明线面垂直；（2）建立空间直角坐标系，利用空间向量进行求解二面角的余弦值.

【详解】（1）连接

∵，，，

∴由余弦定理得：，

∴，∴，

又侧面，平面，∴，

又，，面，∴平面；

（2）由题意及（1）中的垂直关系，以为原点，，，所在直线分别为，，轴，建立如图所示的空间直角坐标系，

则，，，，，

则，，

设平面的一个法向量为，

则，即，

令，得，，所以

设平面的一个法向量为，

则，即，

令，求得

，

∴由图知二面角为锐角，故其余弦值为

19．小张举办了一次抽奖活动.顾客花费3元钱可获得一次抽奖机会.每次抽奖时，顾客从装有1个黑球，3个红球和6个白球（除颜色外其他都相同）的不透明的袋子中依次不放回地摸出3个球，根据摸出的球的颜色情况进行兑奖.顾客中一等奖，二等奖，三等奖，四等奖时分别可领取的奖金为元，10元，5元，1元.若经营者小张将顾客摸出的3个球的颜色分成以下五种情况：个黑球2个红球；个红球；恰有1个白球；恰有2个白球；个白球，且小张计划将五种情况按发生的机会从小到大的顺序分别对应中一等奖，中二等奖，中三等奖，中四等奖，不中奖.

（1）通过计算写出中一至四等奖分别对应的情况（写出字母即可）；

（2）已知顾客摸出的第一个球是红球，求他获得二等奖的概率；

（3）设顾客抽一次奖小张获利元，求变量的分布列；若小张不打算在活动中亏本，求的最大值.

【答案】(1)中一至四等奖分别对应的情况是.(2);(3)194.

【分析】（1）求出一至四等奖的概率，即可写出分别对应的类别；

（2）顾客摸出的第一个球是红球的条件下，利用条件概率计算公式即可得出他获得二等奖的概率．

（3）若经营者不打算在这个游戏的经营中亏本，求出分布列得到期望，即可求a的最大值．

【详解】（1）；，，

，

∵，

∴中一至四等奖分别对应的情况是.

（2）记事件为顾客摸出的第一个球是红球，事件为顾客获得二等奖，则.

（3）的取值为，则分布列为

由题意得，若要不亏本，则，

解得，即的最大值为194.

【点睛】求解该类问题，首先要正确理解题意，其次要准确无误的找出随机变量的所以可能值，计算出相应的概率，写出随机变量的分布列，正确运用均值、方差的公式进行计算，也就是要过三关：（1）阅读理解关；（2）概率计算关；（3）公式应用关.

20．已知椭圆：的离心率为，，分别为椭圆的左、右焦点，过且与轴垂直的直线与椭圆交于点，，且的面积为．

(1)求椭圆的标准方程；

(2)设直线与椭圆交于不同于右顶点的，两点，且，判断直线是否过定点，并说明理由．

【答案】(1)

(2)直线l恒过点，理由见解析

【分析】（1）由题知，，，进而解方程即可得答案；

（2）根据题意设直线的方程为，设，，进而直线方程与椭圆方程联立得，，再根据解方程得，再根据直线方程判断即可.

【详解】（1）解：因为椭圆的离心率为，所以 ①．

将代入，得，

所以，则，即 ②．

又因为，

所以，，

所以椭圆的标准方程为．

（2）解：由题意知，直线的斜率不为0，则不妨设直线的方程为．

联立得消去得，

，化简整理，得．

设，，则，．

因为，所以．

因为，

所以，，

所以，，

将，代入上式整理得，

所以，，解得或（舍去），

所以直线的方程为，则直线恒过点.

21．已知函数（）

(1)当时，有两个实根，求取值范围；

(2)若方程有两个实根，且，证明：

【答案】(1)取值范围是

(2)证明见解析

【分析】（1）利用导数求得的单调区间，由此求得的取值范围.

（2）将方程有两个实根转化为有两个不相等的零点，由此列方程，将证明转化为证明，解得或导数证得不等式成立.

【详解】（1）的定义域为，

，

在上单调递增，所以的取值范围是.

（2）的定义域为，

有两个不相等的实数根，

令，由（1）知在上递增，则，

则有两个不相等的零点，，

，.

要证，只需证，即证，

即证，

，

故只需证，

不妨设，令，

则只需证，

只需证，

令，

，

所以，

即当时，成立.

所以，即，所以.

【点睛】利用导数证明不等式，主要的方法是通过已知条件，划归与转化所要证明的不等式，然后通过构造函数法，结合导数来求所构造函数的取值范围来证得不等式成立.

22．在平面直角坐标系中，直线的参数方程为（为参数）.以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为，点的极坐标为.

（1）求曲线的直角坐标方程和点的直角坐标；

（2）设直线与曲线交于，两点，线段的中点为，求.

【答案】（1）；；（2）.

【解析】（1）直接由极坐标与直角坐标的互化公式化简，即可得到曲线的直角坐标方程和点的直角坐标；

（2）将直线的参数方程代入曲线的直角坐标方程中，得，设有向线段，与实数，对应，则，就是上述方程的两个实根，，从而可得

【详解】解：（1）：，

所以，曲线的直角坐标方程是.

点的极坐标为，化为直角坐标得

（2）将直线的参数方程代入中，

整理得，，此方程有不等实数根.

直线经过定点.

设有向线段，与实数，对应，则，就是上述方程的两个实根，.

已知是线段的中点，对应于参数取值，

所以.

【点睛】关键点点睛：此题考查极坐标与直角坐标的互化，解题的关键是正确利用互化公式，考查直线参数方程的几何意义的应用，直线的参数方程代入曲线方程中化简后要注意判别式的计算，在第二问的解题中关键是准确理解参数几何意义，考查学生的计算能力，属于中档题.

23．已知函数，.

（1）当时，解不等式；

（2）当时，恒成立，求实数的取值范围.

【答案】（1）；（2）.

【解析】（1）对分、、三种情况讨论得解；

（2）等价于，对分、两种情况讨论得解.

【详解】（1）当时，不等式，等价于

当时，不等式化为，即，解集为；

当时，不等式化为，解得；

当时，不等式化为，即，解集为；

综上，所求不等式的解集为.

（2）当时，

等价于，

若，则，∴

若，则，∴

综上，实数的取值范围为.

【点睛】本题主要考查绝对值不等式的解法，考查绝对值三角不等式的应用，意在考查学生对这些知识的理解掌握水平.