山东省烟台龙口市（五四制）2022-2023学年九年级上学期期末考试数学试题(含答案)

2022—2023学年第一学期期末阶段性测试

                       初四数学试题 (120分钟)

一、选择题（本题共10个小题，每小题3分，满分30分）

1.二次函数y=x2+2x-1的图象与y轴的交点坐标是

A．（0，-1）  B．（0，-2） C．（-1，0） D．（-2，0）

2.若sin（70°-α）=cos50°，则α的度数是

A．50°  B．40° C．30° D．20°

3.如图所示的几何体，其左视图是

4.已知⊙O的半径为3，OP=5，则点P与⊙O的位置关系是

A．点P在⊙O外   B．点P在⊙O上  C．点P在⊙O内 D．不能确定

5.为解决“在甲、乙两个不透明口袋中随机摸球”的问题，小明列出表格如表所示，已知这些球除颜色外无其他差别，小明从两个口袋中各随机取出一个球，则取出的球是一个红球和一个白球的概率为

A．   B． 

C．   D．

6.已知cosA=0.5592，运用科学计算器在开机状态下求锐角A时，按下的第一个键是

A.          B.         C.          D.

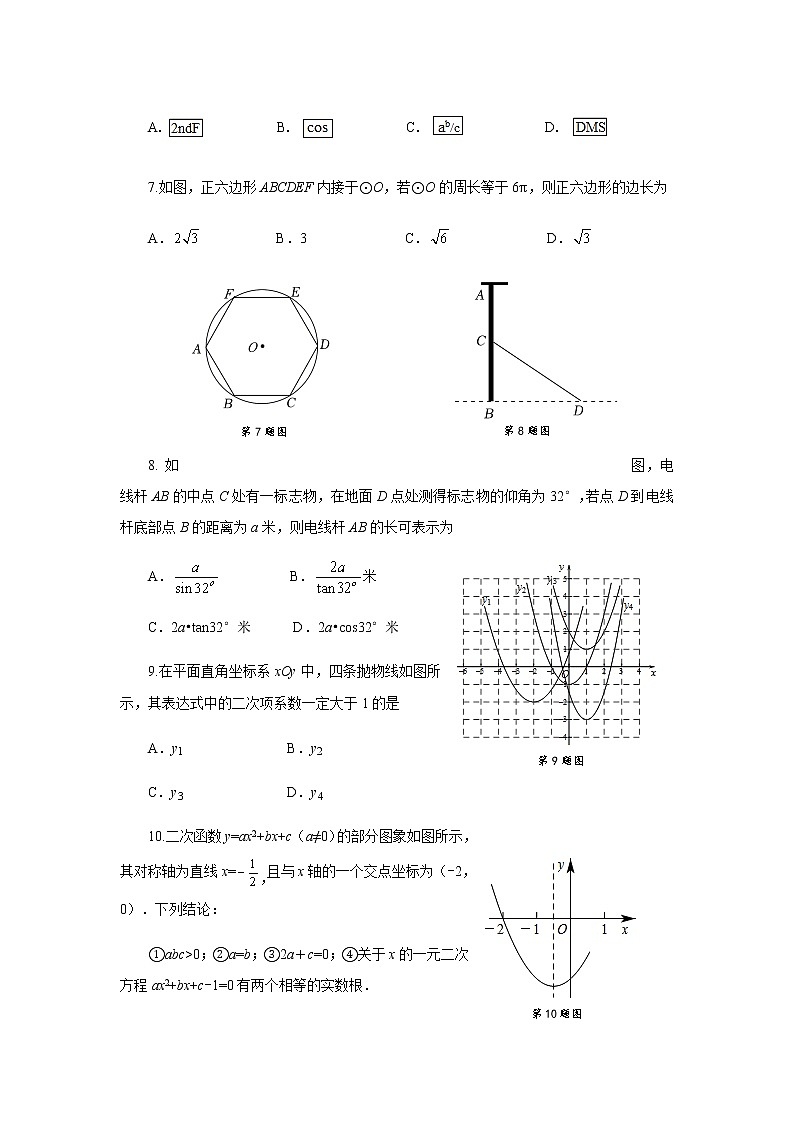
7.如图，正六边形ABCDEF内接于⊙O，若⊙O的周长等于6π，则正六边形的边长为

A．  B．3              C． D．

8.如图，电线杆AB的中点C处有一标志物，在地面D点处测得标志物的仰角为32°，若点D到电线杆底部点B的距离为a米，则电线杆AB的长可表示为

A．          B．米 

C．2a•tan32°米      D．2a•cos32°米

9.在平面直角坐标系xOy中，四条抛物线如图所示，其表达式中的二次项系数一定大于1的是

A．y1   B．y2 

C．y3   D．y4

10.二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，其对称轴为直线x=，且与x轴的一个交点坐标为（-2，0）．下列结论：

①abc>0；②a=b；③2a＋c=0；④关于x的一元二次方程ax2+bx+c-1=0有两个相等的实数根．

其中正确结论的序号是

A．①③              B．②③       

C．②④              D．③④

二、填空题（本大题共6个小题，每小题3分，满分18分）

11.写一个开口向上且过坐标原点的二次函数表达式

                   .

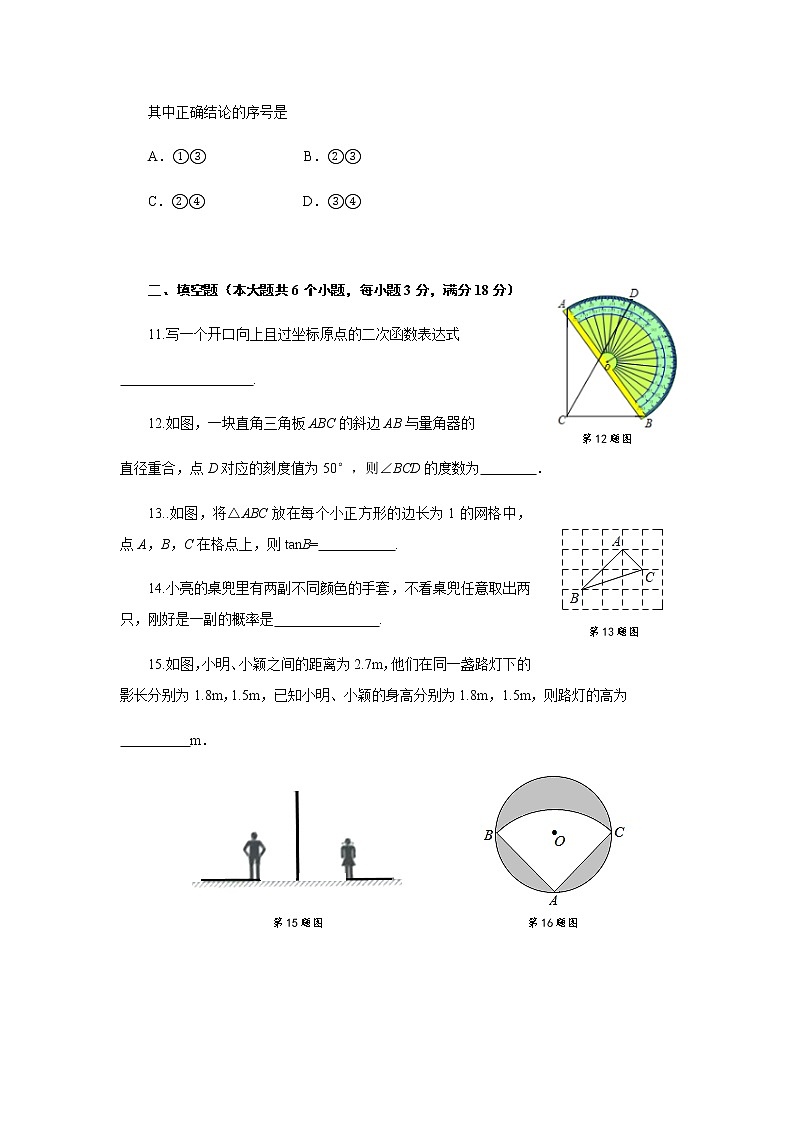
12.如图，一块直角三角板ABC的斜边AB与量角器的

直径重合，点D对应的刻度值为50°，则∠BCD的度数为　    　．

13..如图，将△ABC放在每个小正方形的边长为1的网格中，点A，B，C在格点上，则tanB=           .  

14.小亮的桌兜里有两副不同颜色的手套，不看桌兜任意取出两只，刚好是一副的概率是               .

15.如图，小明、小颖之间的距离为2.7m，他们在同一盏路灯下的影长分别为1.8m，1.5m，已知小明、小颖的身高分别为1.8m，1.5m，则路灯的高为

　      　m．

16.如图，有一直径是米的圆形铁皮，现从中剪出一个圆心角是90°的最大扇形ABC，若用该扇形铁皮围成一个圆锥，则所得圆锥的底面圆的半径为             ．

三、解答题（本大题共9个小题，满分72分）

17.（本题满分5分）

计算：2cos30°-+

18.（本题满分5分）

已知抛物线y=x2+bx+c经过点（-1，0），（3，0）．

（1）求该抛物线的对称轴．

（2）自变量x在什么范围内时，y的值随x值的增大而减小？

19.（本题满分6分）

如图，身高1.5米的小明（AB）在太阳光下的影子AG长1.8米，此时，立柱CD的影子一部分落在地面CE上，一部分落在墙EF上．

（1）请你在墙上画出表示CD的部分影子EH；

（2）若量得CE=1.2米，EH=1.5米，求立柱CD的高．

20.（本题满分6分）

如图，AB是⊙O的直径，CD是⊙O的一条弦，且CD⊥AB于点E．

（1）求证：∠BCO=∠D；

（2）若CD=4，OE=1，求⊙O的半径．

21.（本题满分7分）

如图所示，甲、乙两人玩游戏，他们准备了1个可以自由转动的转盘和一个不透明的袋子．转盘被分成面积相等的三个扇形，并在每一个扇形内分别标上数字-1，-2，-3；袋子中装有除数字以外其它均相同的三个乒乓球，球上标有数字1，2，3．游戏规则：转动转盘，当转盘停止后，指针所指区域的数字与随机从袋中摸出乒乓球的数字之和为0时，甲获胜；其它情况乙获胜．（如果指针恰好指在分界线上，那么重转一次，直到指针指向某一区域为止）

（1）利用树状图求甲获胜的概率；

（2）这个游戏规则对甲乙双方公平吗？请判断并说明理由．

22.（本题满分8分）

尺规作图：（不写作法，保留作图痕迹）

已知：⊙O和⊙O外一点P．

求作：过点P的⊙O的切线PA，PB．

23.（本题满分8分）

某大型超市为缓解停车难问题，建筑设计师提供了楼顶停车场的设计示意图．按规定，停车场坡道口上坡要张贴限高标志，以便告知车辆能否安全驶入．请根据如图，求出汽车通过坡道口的限高DF的长（结果精确到0.1m，sin28°≈0.47，cos28°≈0.88，tan28°≈0.53）．

24.（本题满分12分）

如图，△ABC中，AB=AC，点D为BC上一点，且AD=DC，过A，B，D三点作⊙O，AE是⊙O的直径，连接DE．

（1）求证：AC是⊙O的切线；

（2）若cosC=，AC=24，求直径AE的长．

25.（本题满分15分）

如图，在平面直角坐标系内，抛物线y=ax2+bx-4（a≠0）与x轴交于点A，点B，与y轴交于点C．过点A的直线y=x+2与抛物线交于点E，且点E的横坐标为6．点P为第四象限内抛物线上的一个动点．

（1）求抛物线的表达式；

（2）在点P的运动过程中，是否存在点P使得△AEP的面积最大，求这个最大值和点P的坐标；

（3）在（2）的条件下，在x轴上求点Q，使以A，P，Q为顶点的三角形与△ABE相似．

2022-2023学年第一学期期末阶段性测试

初四数学参考答案及评分意见

一、选择题（每小题3分，共30分）

二、填空题（每小题3分，共18分）

11.答案不唯一，如y=2x2+x， 12.65°， 13.， 14.，15.3， 16..

三、解答题（17-18题每题5分，19-20题每题6分，21题7分，22-23题每题8分，24题12分，25题15分，共72分）

17.解：原式=2×-+1-=-1+1-=．

18.解：（1）∵抛物线y=x2+bx+c经过点（-1，0），（3，0），故.

∴抛物线的对称轴为直线x=1；

（2）∵抛物线的对称轴为直线x=1，且a＞0，开口向上，

∴x＜1时，y的值随x值的增大而减小．

19.解（1）如右图，线段EH为所求．

（2）过点E作EM∥BG，交CD于点M，

则四边形DHEM是平行四边形，即DM=EH=1.5，

∵，∴，∴CM=1，

∴CD=CM+DM=1+1.5=2.5（米），

故立柱CD的高为2.5米．

20.（1）证明：∵OC=OB，∴∠BCO=∠B.

∵∠B=∠D，∴∠BCO=∠D；

（2）解：∵AB是⊙O的直径，且CD⊥AB于点E，∴CE=CD，

∵CD=4，∴CE=.

在Rt△OCE中，OC2=CE2+OE2，∵OE=1，∴，解得OC=3（取正值），

∴⊙O的半径为3．

21.解：（1）树状图如右图，

总共有9种可能的结果，每种结果出现的可能性相同，其中两数之和为0的结果有3种，即（-1，1），（-2，2），（-3，3）.

∴P（甲获胜）=；

（2）游戏不公平，

∵P（甲获胜）=，P（乙获胜）=，

∴P（甲获胜）≠P（乙获胜），

∴游戏不公平．

22.解：（1）作图如右图，

直线PA、PB即为所作的⊙O的切线；

23.解：在Rt△ABC中，∠A=28°，AC=10，

∴BC=ACtan28°≈10×0.53=5.3，

∴BD=BC-CD=5.3-0.5=4.8.

在Rt△BDF中，∠BDF=∠A=28°，BD=4.8，

∴DF=BDcos28°≈4.8×0.88=4.224≈4.2.

答：坡道口的限高DF的长是4.2m．

24.解：（1）∵AB=AC，AD=DC，∴∠C=∠B，∠1=∠C，

∴∠1=∠B.

又∵∠E=∠B，

∴∠1=∠E.

∵AE是⊙O的直径，

∴∠ADE=90°，∴∠E+∠EAD=90°，

∴∠1+∠EAD=90°，即∠EAC=90°，

∴AE⊥AC，

∴AC是⊙O的切线；

（2）如图，过点D作DF⊥AC于点F，

∵DA=DC，∴CF=AC=12.

在Rt△CDF中，∵cosC=，∴=，即=，

解得DC=20，∴DF=16．

∴AD=20.

∵∠ADE=∠DFC=90°，∠E=∠C，

∴△ADE∽△DFC，

∴，即，

解得AE=25．

25.解：（1）令y=0，则x=-2，

∴A点坐标为（-2，0）.

当x=6时，

y=6+2=8.

∴E点坐标为（6，8）.

将（-2，0），（6，8）分别代入y=ax2+bx-4，得

∴

解得

∴y=x2-x-4；

（2）存在点P使得△AEP的面积最大，

理由如下：

过P点作PG∥y轴交AE于G，

设P（t，t2-t-4），则G（t，t+2），

∴PG=-t2+2t+6，

∴S△APE=×（2+6）×（-t2+2t+6）=-2（t-2）2+32，

当t=2时，△AEP的面积最大为32，

此时P（2，-4）；

（3）由抛物线的表达式可知B（4，0），

∵A（-2，0），E（6，8），

∴AE=8，BE=2，AB=6，

∵P（2，-4），

∴AP=4.

过点E作EK⊥x轴交于K点，过点P作PH⊥x轴交于点H，

∴AK=EK=8，AH=PH=4，

∴∠EAB=∠BAP=45°，

当∠AQP=∠ABE时，△ABE∽△AQP，

∴，

∴，

∴AQ=3，

∴Q（1，0）.

当∠APQ=∠ABE时，△ABE∽△APQ，

∴，

∴，

∴AQ=，

∴Q（，0）；

综上所述，Q点坐标为（1，0）或（，0）．