专题 18.41 特殊平行四边形中考真题专练（巩固篇）（专项练习）-八年级数学下册基础知识专项讲练（人教版）

这是一份专题 18.41 特殊平行四边形中考真题专练（巩固篇）（专项练习）-八年级数学下册基础知识专项讲练（人教版），共44页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

专题 18.41 特殊平行四边形中考真题专练（巩固篇）
（专项练习）
一、单选题
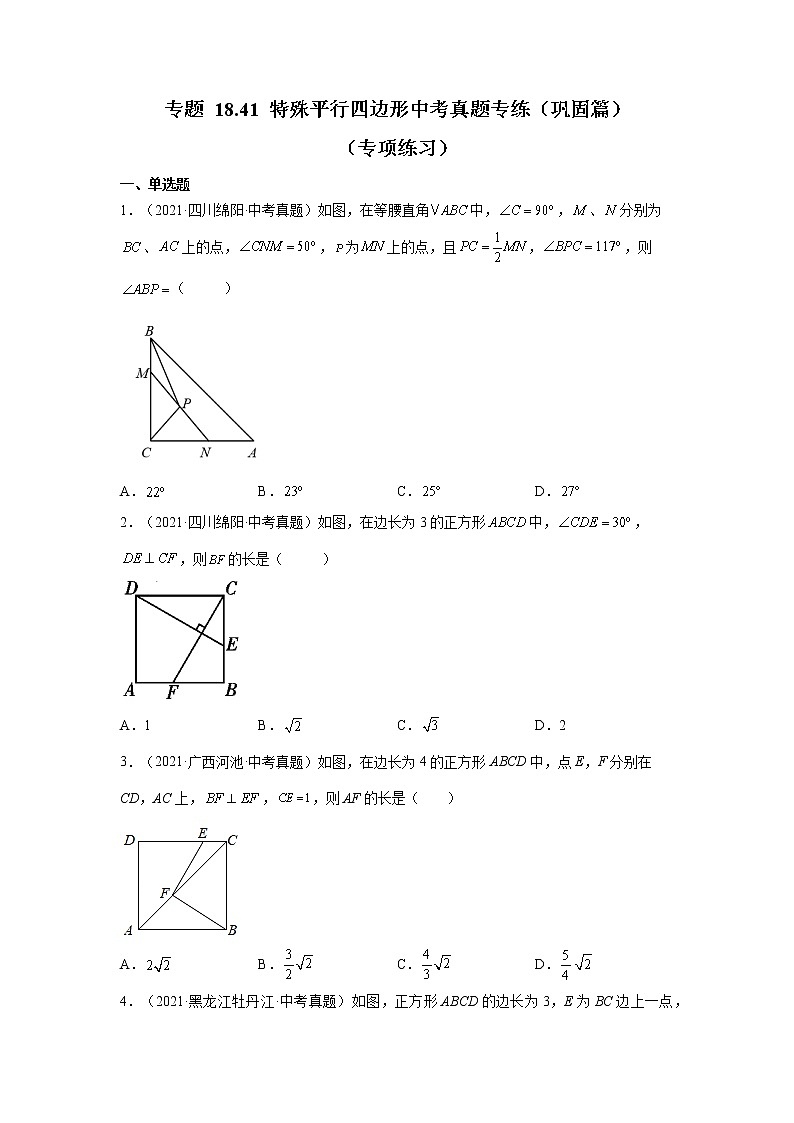
1．（2021·四川绵阳·中考真题）如图，在等腰直角中，，、分别为、上的点，，为上的点，且，，则（       ）

A． B． C． D．
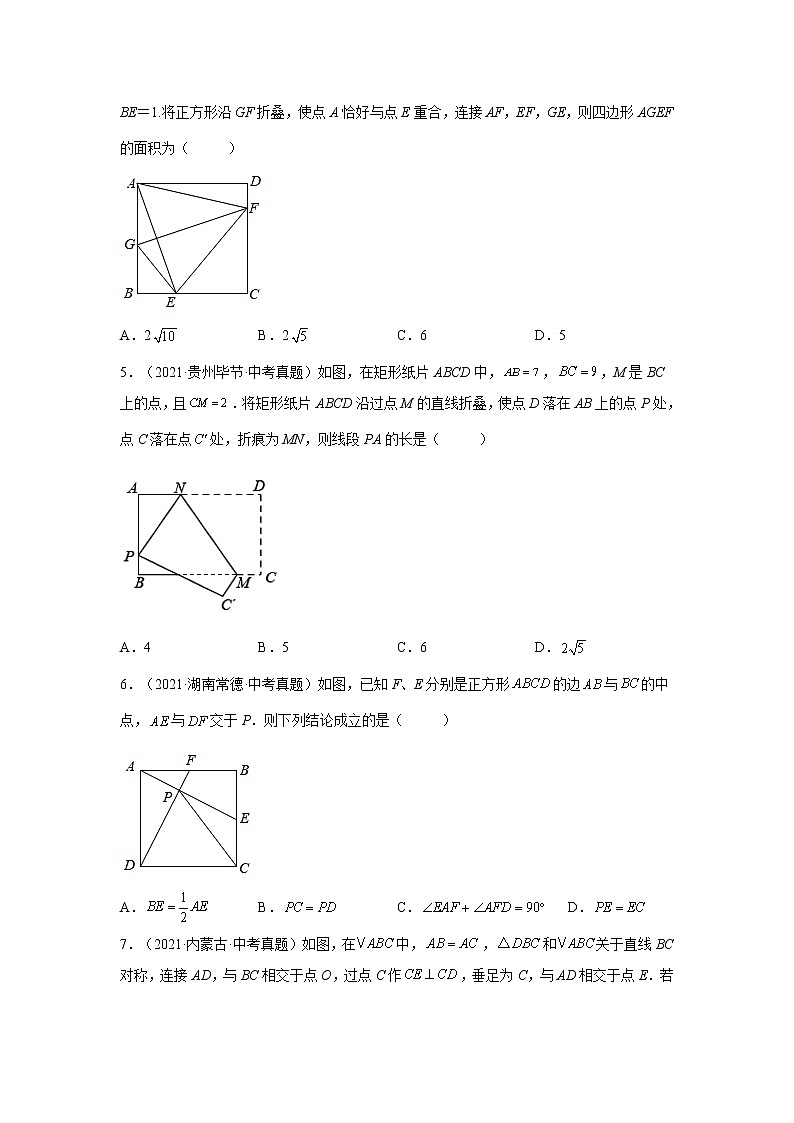
2．（2021·四川绵阳·中考真题）如图，在边长为3的正方形中，，，则的长是（       ）

A．1 B． C． D．2
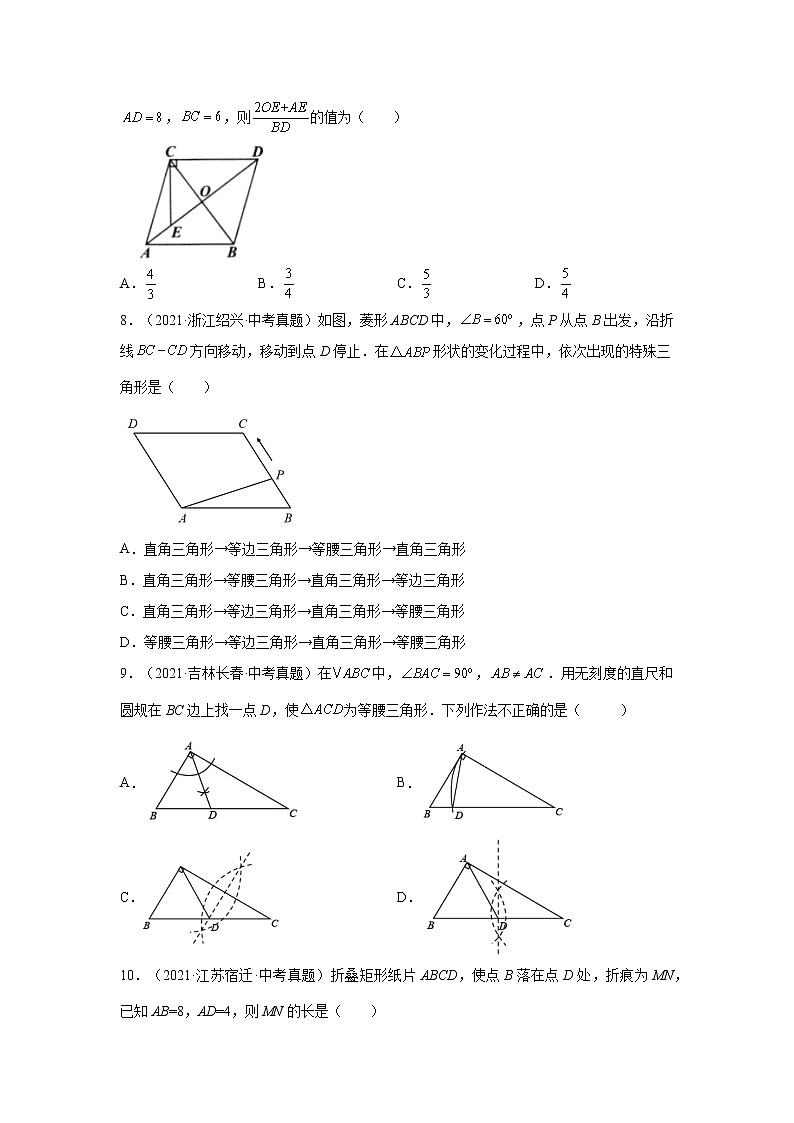
3．（2021·广西河池·中考真题）如图，在边长为4的正方形ABCD中，点E，F分别在CD，AC上，，，则AF的长是（     ）

A． B． C． D．
4．（2021·黑龙江牡丹江·中考真题）如图，正方形ABCD的边长为3，E为BC边上一点，BE＝1.将正方形沿GF折叠，使点A恰好与点E重合，连接AF，EF，GE，则四边形AGEF的面积为（       ）

A．2 B．2 C．6 D．5
5．（2021·贵州毕节·中考真题）如图，在矩形纸片ABCD中，，，M是BC上的点，且．将矩形纸片ABCD沿过点M的直线折叠，使点D落在AB上的点P处，点C落在点处，折痕为MN，则线段PA的长是（       ）

A．4 B．5 C．6 D．
6．（2021·湖南常德·中考真题）如图，已知F、E分别是正方形的边与的中点，与交于P．则下列结论成立的是（       ）

A． B． C． D．
7．（2021·内蒙古·中考真题）如图，在中，，和关于直线BC对称，连接AD，与BC相交于点O，过点C作，垂足为C，与AD相交于点E．若，，则的值为（     ）

A． B． C． D．
8．（2021·浙江绍兴·中考真题）如图，菱形ABCD中，，点P从点B出发，沿折线方向移动，移动到点D停止．在形状的变化过程中，依次出现的特殊三角形是（     ）

A．直角三角形→等边三角形→等腰三角形→直角三角形
B．直角三角形→等腰三角形→直角三角形→等边三角形
C．直角三角形→等边三角形→直角三角形→等腰三角形
D．等腰三角形→等边三角形→直角三角形→等腰三角形
9．（2021·吉林长春·中考真题）在中，，．用无刻度的直尺和圆规在BC边上找一点D，使为等腰三角形．下列作法不正确的是（       ）
A． B．
C． D．
10．（2021·江苏宿迁·中考真题）折叠矩形纸片ABCD，使点B落在点D处，折痕为MN，已知AB=8，AD=4，则MN的长是（     ）
A． B．2 C． D．4
11．（2021·陕西·中考真题）如图，在菱形中，，连接、，则的值为（     ）

A． B． C． D．
12．（2021·广西河池·中考真题）已知平行四边形ABCD，下列条件中，不能判定这个平行四边形为矩形的是（　　）
A．∠A=∠B B．∠A=∠C C．AC=BD D．AB⊥BC
二、填空题
13．（2021·辽宁鞍山·中考真题）如图，，定长为a的线段端点A，B分别在射线OP，OQ上运动（点A，B不与点O重合），C为AB的中点，作关于直线OC对称的，交AB于点D，当是等腰三角形时，的度数为_____________．

14．（2021·辽宁锦州·中考真题）如图，在矩形ABCD中，AB＝6，BC＝10，以点B为圆心、BC的长为半径画弧交AD于点E，再分别以点C，E为圆心、大于CE的长为半径画弧，两弧交于点F，作射线BF交CD于点G，则CG的长为__________________．

15．（2021·江苏徐州·中考真题）如图，四边形与均为矩形，点分别在线段上．若，矩形的周长为，则图中阴影部分的面积为___________．

16．（2021·贵州毕节·中考真题）如图，在菱形ABCD中，，，Q为AB的中点，P为对角线BD上的任意一点，则的最小值为_____________．

17．（2021·辽宁大连·中考真题）如图，在菱形中，，点E在边上，将沿直线翻折180°，得到，点B的对应点是点若，，则的长是__________．

18．（2021·江苏常州·中考真题）中国古代数学家刘徽在《九章算术注》中，给出了证明三角形面积公式的出入相补法．如图所示，在中，分别取、的中点D、E，连接，过点A作，垂足为F，将分割后拼接成矩形．若，则的面积是__________．

19．（2021·内蒙古·中考真题）如图，BD是正方形ABCD的一条对角线，E是BD上一点，F是CB延长线上一点，连接CE，EF，AF．若，，则的度数为__________．

20．（2021·山东枣庄·中考真题）如图，，，点在上，四边形是矩形，连接，交于点，连接交于点．下列4个判断：①；②；③；④若点是线段的中点，则为等腰直角三角形，其中，判断正确的是______．（填序号）

21．（2021·江苏盐城·中考真题）如图，在矩形中，，，、分别是边、上一点，，将沿翻折得，连接，当________时，是以为腰的等腰三角形．

22．（2021·山西·中考真题）如图，在菱形中，对角线，相交于点，，，，交于点，则的长为__________．

三、解答题
23．（2021·辽宁丹东·中考真题）如图，在中，点O是的中点，连接并延长交的延长线于点E，连接、．
（1）求证：四边形是平行四边形；
（2）若，判断四边形的形状，并说明理由．




24．（2021·新疆·中考真题）如图，在矩形ABCD中，点E在边BC上，点F在BC的延长线上，且．
求证：（1）；
（2）四边形AEFD是平行四边形．



25．（2021·吉林·中考真题）如图①，在中，，，是斜边上的中线，点为射线上一点，将沿折叠，点的对应点为点．
（1）若．直接写出的长（用含的代数式表示）；
（2）若，垂足为，点与点在直线的异侧，连接，如图②，判断四边形的形状，并说明理由；
（3）若，直接写出的度数．





26．（2021·山东济宁·中考真题）研究立体图形问题的基本思路是把立体图形问题转化为平面图形问题．
（1）阅读材料
立体图形中既不相交也不平行的两条直线所成的角，就是将直线平移使其相交所成的角．
例如，正方体（图1）．因为在平面中，，与相交于点A，所以直线与所成的就是既不相交也不平行的两条直线与所成的角．
解决问题
如图1，已知正方体，求既不相交也不平行的两条直线与所成角的大小．


（2）如图2，M，N是正方体相邻两个面上的点．
①下列甲、乙、丙三个图形中，只有一个图形可以作为图2的展开图，这个图形是 ；
②在所选正确展开图中，若点M到，的距离分别是2和5，点N到，的距离分别是4和3，P是上一动点，求的最小值．




27．（2021·湖北荆门·中考真题）如图，点E是正方形ABCD的边BC上的动点，，且，．
（1）求证：；
（2）若，，用x表示DF的长．

28．（2021·辽宁阜新·中考真题）在图1中似乎包含了一些曲线，其实它们是由多条线段构成的．它不但漂亮，还蕴含着很多美妙的数学结论．如图，在正方形ABCD中，E，F分别是直线AB，BC上的点（E，F在直线AC的两侧），且．
（1）如图2，求证：；
（2）若直线AC与EF相交于点G，如图3，求证：；
（3）设正方形ABCD的中心为O，，用含的式子表示的度数（不必证明）．

























参考答案
1．A
【解析】
【分析】作辅助线，构建矩形，得P是MN的中点，则MP＝NP＝CP，根据等腰三角形的性质和三角形外角的性质可解答．
【详解】
解：如图，过点M作MG⊥BC于M，过点N作NG⊥AC于N，连接CG交MN于H，

∴∠GMC＝∠ACB＝∠CNG＝90°，
∴四边形CMGN是矩形，
∴CH＝CG＝MN，
∵PC＝MN，
存在两种情况：
如图，CP＝CP1＝MN，

①P是MN中点时，
∴MP＝NP＝CP，
∴∠CNM＝∠PCN＝50°，∠PMN＝∠PCM＝90°−50°＝40°，
∴∠CPM＝180°−40°−40°＝100°，
∵△ABC是等腰直角三角形，
∴∠ABC＝45°，
∵∠CPB＝117°，
∴∠BPM＝117°−100°＝17°，
∵∠PMC＝∠PBM＋∠BPM，
∴∠PBM＝40°−17°＝23°，
∴∠ABP＝45°−23°＝22°．
②CP1＝MN，
∴CP＝CP1，
∴∠CPP1＝∠CP1P＝80°，
∵∠BP1C＝117°，
∴∠BP1M＝117°−80°＝37°，
∴∠MBP1＝40°−37°＝3°，
而图中∠MBP1＞∠MBP，所以此种情况不符合题意．
故选：A．
【点拨】此题主要考查了等腰直角三角形的性质，矩形的性质和判定，等腰三角形的性质等知识，作出辅助线构建矩形CNGM证明P是MN的中点是解本题的关键．
2．C
【解析】
【分析】由正方形的性质得出，，由证得，即可得出答案．
【详解】
解：四边形是正方形，

，，
∵在中，，
，
设，则，
根据勾股定理得：，
即，
解得：（负值舍去），
，
，
，
，
，
，，
，
．
故选：．
【点拨】本题考查了正方形的性质，全等三角形的判定与性质，勾股定理，含角的直角三角形的性质等知识，证明是解题的关键．
3．B
【解析】
【分析】过作的垂线分别交于,由，证明，设，根据，求得，在中，利用勾股定理即可求得．
【详解】
如图，过作的垂线分别交于，

四边形是正方形，
，
，
四边形是矩形，
，，
，
，
，
，
四边形是正方形，
，
，
，
在和中，

（AAS），
，
设，则，
，
即，
解得，
，
四边形是正方形，，
，
，
．
故选B
【点拨】本题考查了矩形的性质，正方形的性质，三角形全等的性质与判定，勾股定理，等腰直角三角形的性质，求得是解题的关键．
4．D
【解析】
【分析】作FH⊥AB于H，交AE于P，设AG=GE=x，在Rt△BGE中求出x，在Rt△ABE中求出AE，再证明△ABE≌△FHG，得到FG=AE，然后根据S四边形AGEF=S△AGF+S△EGF求解即可
【详解】
解：作FH⊥AB于H，交AE于P，则四边形ADFH是矩形，由折叠的性质可知，AG=GE，AE⊥GF，AO=EO．
设AG=GE=x，则BG=3-x，
在Rt△BGE中，
∵BE2+BG2=GE2，
∴12+(3-x)2=x2，
∴x=．
在Rt△ABE中，
∵AB2+BE2=AE2，
∴32+12=AE2，
∴AE=．
∵∠HAP+∠APH=90°，∠OFP+∠OPF=90°，∠APH=∠OPF，
∴∠HAP=∠OFP，
∵四边形ADFH是矩形，
∴AB=AD=HF．
在△ABE和△FHG中，
，
∴△ABE≌△FHG，
∴FG=AE=，
∴S四边形AGEF=S△AGF+S△EGF
=
=
=
=
=5．
故选D．

【点拨】本题考查了折叠的性质，正方形的性质，矩形的判定与性质，三角形的面积，以及勾股定理等知识，熟练掌握折叠的性质是解答本题的关键．
5．B
【解析】
【分析】连接PM，证明即可得到，PA=5．
【详解】
连接PM

∵矩形纸片ABCD中，，，
∴
∵
∴
∵折叠
∴,
∴
∵PM=PM
∴
∴
∴
故选B．
【点拨】本题考查矩形的折叠问题，解题的关键是看到隐藏条件，学会利用翻折不变性解决问题．
6．C
【解析】
【分析】根据正方形的性质，全等三角形的判定和性质以及等腰三角形的性质逐一判断即可．
【详解】
解：∵四边形ABCD是正方形，
∴AB=BC=CD=CA，∠ABC=∠BCD=∠CDA=∠DAB=90°，
∵已知F、E分别是正方形ABCD的边AB与BC的中点，
∴BE=BC=AB 在△ABE和△DAF中，
，
∴△ABE≌△DAF（SAS），
∴∠BAE=∠ADF，
∵∠ADF+∠AFD=90°，
∴∠BAE+∠AFD =90°，
∴∠APF=90°，
∴∠EAF+∠AFD=90°，故C选项正确，符合题意；
连接FC，

同理可证得△CBF≌△DAF（SAS），
∴∠BCF=∠ADF，
∴∠BCD-∠BCF=∠ADC-∠ADF，即90°-∠BCF=90°-∠ADF，
∴∠PDC=∠FCD>∠PCD，
∴PC>PD，故B选项错误，不符合题意；
∵AD>PD，
∴CD>PD，
∴∠DPC>∠DCP，
∴90°-∠DPC<90°-∠DCP，
∴∠CPE<∠PCE，
∴PE> CE，故D选项错误，不符合题意；
故选：C．
【点拨】本题考查了正方形的性质，全等三角形的判定与性质，等腰三角形的性质等知识．此题综合性很强，解题的关键是注意数形结合思想的应用．
7．D
【解析】
【分析】根据，和关于直线BC对称，证明出四边形ABDC是菱形，再根据菱形的性质得到BC⊥AD，OC=OB，OA=OD，最后由勾股定理求出结果．
【详解】
解：∵，和关于直线BC对称，
∴AB=AC=CD=BD，
∴四边形ABDC是菱形，
∴BC⊥AD，OC=OB，OA=OD，
∵，，
∴OC=OB=3，OA=OD=4，
在Rt△COD中，OC=3，OD=4，
∴DC=，
∴AB=AC=CD=BD =5，
∵，
∴，，
∴，
∴，
∴，
故选：D．
【点拨】本题主要考查了等腰三角形的性质、折叠的性质、菱形的判定与性质以及勾股定理，关键在于利用等腰三角形与折叠的性质证明出四边形是菱形，再用菱形的性质与勾股定理进行求解．
8．C
【解析】
【分析】是特殊三角形，取决于点P的某些特殊位置，按其移动方向，逐一判断即可．
【详解】
解：连接AC，BD，如图所示．
∵四边形ABCD是菱形，
∴AB=BC=CD=DA，∠D=∠B．
∵∠B=60°，
∴∠D=∠B=60°．
∴和都是等边三角形．
点P在移动过程中，依次共有四个特殊位置：

（1）当点P移动到BC边的中点时，记作．
∵是等边三角形，是 BC的中点，
∴．
∴．
∴是直角三角形．
（2）当点P与点C重合时，记作．
此时，是等边三角形；
（3）当点P移动到CD边的中点时，记为．
∵和都是等边三角形，
∴．
∴是直角三角形．
（4）当点P与点D重合时，记作．
∵，
∴是等腰三角形．
综上，形状的变化过程中，依次出现的特殊三角形是：
直角三角形→等边三角形→直角三角形→等腰三角形．
故选：C
【点拨】本题考查了菱形的性质、直角三角形的判定、等腰三角形的判定、等边三角形的性质与判定等知识点，熟知特殊三角形的判定方法是解题的关键．
9．A
【解析】
【分析】利用直角三角形的性质、中垂线的性质、角平分线的尺规作图逐一判断即可得．
【详解】
解：A．此作图是作∠BAC平分线，在中，，，无法得出为等腰三角形，此作图不正确，符合题意；
B．此作图可直接得出CA＝CD，即为等腰三角形，此作图正确，不符合题意；
C．此作图是作AC边的中垂线，可直接得出AD＝CD，此作图正确，不符合题意；
D．此作图是作BC边的中垂线，可知AD是BC上的中线，为等腰三角形，此作图正确，不符合题意；
故选：A．
【点拨】本题主要考查作图−基本作图，解题的关键是掌握直角三角形的性质、中垂线的性质、角平分线的尺规作图．
10．B
【解析】
【分析】连接BM，利用折叠的性质证明四边形BMDN为菱形，设DN＝NB＝x，在RtABD中，由勾股定理求BD，在RtADN中，由勾股定理求x，利用菱形计算面积的两种方法，建立等式求MN．
【详解】
解：如图，连接BM，

由折叠可知，MN垂直平分BD，

又AB∥CD，

∴BON≌DOM，
∴ON＝OM，
∴四边形BMDN为菱形（对角线互相垂直平分的四边形是菱形），

设DN＝NB＝x，则AN＝8﹣x，
在RtABD中，由勾股定理得：BD＝＝，
在RtADN中，由勾股定理得：AD2+AN2＝DN2，
即42+（8﹣x）2＝x2，
解得x＝5，
根据菱形计算面积的公式，得
BN×AD＝×MN×BD，
即5×4＝×MN×，
解得MN＝．
故选：B．
【点拨】本题考查图形的翻折变换，勾股定理，菱形的面积公式的运用，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后对应线段相等．
11．D
【解析】
【分析】设AC与BD的交点为O，由题意易得，，进而可得△ABC是等边三角形，，然后问题可求解．
【详解】
解：设AC与BD的交点为O，如图所示：

∵四边形是菱形，
∴，，
∵，
∴△ABC是等边三角形，
∴，
∴，
∴，
∴，
∴；
故选D．
【点拨】本题主要考查菱形的性质、含30°角的直角三角形的性质及勾股定理，熟练掌握菱形的性质、含30°角的直角三角形的性质及勾股定理是解题的关键．
12．B
【解析】
【详解】
【分析】由矩形的判定方法即可得出答案．
【详解】A、∠A=∠B，∠A+∠B=180°，所以∠A=∠B=90°，可以判定这个平行四边形为矩形，正确；
B、∠A=∠C不能判定这个平行四边形为矩形，错误；
C、AC=BD，对角线相等，可推出平行四边形ABCD是矩形，故正确；
D、AB⊥BC，所以∠B=90°，可以判定这个平行四边形为矩形，正确，
故选B．
【点睛】本题考查了矩形的判定，熟练掌握“有一个角是直角的平行四边形是矩形、对角线相等的平行四边形是矩形、有三个角是直角的四边形是矩形”是解题的关键.
13．或
【解析】
【分析】结合折叠及直角三角形斜边中线等于斜边一半的性质可得，设，然后利用三角形外角和等腰三角形的性质表示出，，，，从而利用分类讨论思想解题．
【详解】
解：，C为AB的中点，
，
，，
又由折叠性质可得，
，
设，则，，，，
①当时，，
，
解得，
；
②当时，，
，方程无解，
此情况不存在；
③当时，，
，
解得：，
；
综上，的度数为或，
故答案为：或．
【点拨】此题考查折叠及直角三角形斜边中线等于斜边一半的性质，三角形外角和等腰三角形的性质，难度一般．
14．
【解析】
【分析】根据作图过程可得BF是∠EBC的平分线，然后证明△EBG≌△CBG，再利用勾股定理即可求出CG的长．
【详解】
解：如图，连接EG，

根据作图过程可知：BF是∠EBC的平分线，
∴∠EBG＝∠CBG，
在△EBG和△CBG中，
，
∴△EBG≌△CBG（SAS），
∴GE＝GC，∠BEG=∠C=90°，
在Rt△ABE中，AB＝6，BE＝BC＝10，
∴AE＝＝8，
∴DE＝AD﹣AE＝10﹣8＝2，
在Rt△DGE中，DE＝2，DG＝DC﹣CG＝6﹣CG，EG＝CG，
∴EG2﹣DE2＝DG2
∴CG2﹣22＝（6﹣CG）2，
解得CG＝．
故答案为：．
【点拨】本题考查了矩形的性质，作图-基本作图，解决本题的关键是掌握矩形的性质．
15．
【解析】
【分析】根据矩形性质和矩形周长，得到，然后设，然后根据列出代数式即可求解阴影部分面积．
【详解】
∵矩形的周长为，
∴，
设，则，，，



，
故答案为．
【点拨】本题考查了矩形的性质，和列代数式及整式的化简，关键是读懂题目，列出代数式．
16．
【解析】
【分析】连接AC，CQ，则CQ的长即为AP+PQ的最小值，再根据菱形ABCD中，∠BCD=120°得出∠ABC的度数，进而判断出△ABC是等边三角形，故△BCQ是直角三角形，根据勾股定理即可得出CQ的长．
【详解】
解：连接AC，CQ，

∵四边形ABCD是菱形，
∴A、C关于直线BD对称，
∴CQ的长即为AP+PQ的最小值，
∵∠BCD=120°，
∴∠ABC=60°，
∴△ABC是等边三角形，
∵Q是AB的中点，
∴CQ⊥AB，BQ=BC=×2=1，
∴CQ=．
故答案为：．
【点拨】本题考查了轴对称-最短路线问题，熟知菱形的性质及两点之间线段最短是解答此题的关键．
17．
【解析】
【分析】由题意易得，，则有，进而根据折叠的性质可得，，然后根据三角形内角和可得，最后根据等腰直角三角形的性质可求解．
【详解】
解：∵四边形是菱形，
∴，
∵，
∴，是等边三角形，即，
∵，
∴，
由折叠的性质可得，，，
在中，由三角形内角和可得，
∴，即，
∴是等腰直角三角形，
∴；
故答案为．
【点拨】本题主要考查菱形的性质、折叠的性质及等腰直角三角形的性质与判定，熟练掌握菱形的性质、折叠的性质及等腰直角三角形的性质与判定是解题的关键．
18．12
【解析】
【分析】先证明，，把三角形的面积化为矩形的面积，进而即可求解．
【详解】
解：∵D是的中点，四边形是矩形，
∴AD=BD，∠G=∠AFD=90°，
又∵∠ADF=∠BDG，
∴，
∴DF=DG，AF=BG=2，
同理：，
∴EF=EH，
∴GH=2(DF+EF)=2DE=2×3=6，
∴的面积=矩形的面积=2×6=12．
【点拨】本题主要考查全等三角形的判定和性质，矩形的性质，通过全等三角形的判定，把三角形的面积化为矩形的面积，是解题的关键．
19．
【解析】
【分析】首先连接AE，由题可知，DE=DC=AD,所以△DEC,△AED,△EFC是等腰三角形，由正方形的性质得∠EBC=∠ADE=∠EDC=45°，求出,得出=22.5°，,,所以 ,得出∠AEF=90°，再证明 ,则,所以△AEF为等腰直角三角形，∠FAE=45°，减去∠BAE即可．
【详解】
连接AE,如图，

∵四边形ABCD为正方形，
∴AD=CD,∠ADE=∠EDC=∠CBE=45°， ,
∵DE=CD,
∴AD=DE=CD，
∴∠DAE=∠DEA=∠DEC=∠DCE=67.5°，
∴ , ,
又∵EF=EC,
∴ ,
∴ ,
∴ ,
∴ ,
在△DAE和△DEC中：
∵
∴△DAE≌△DEC(SAS),
∴AE=EC，
又∵EC=EF,
∴AE=EF，
∴△AEF为等腰直角三角形，
∴∠FAE=45°，
∴,
故填：22.5°．
【点拨】本题考查正方形的性质，等腰三角形的性质，全等三角形的判定，三角形内角和，解题关键是添加辅助线，构造全等三角形．
20．①③④
【解析】
【分析】先根据矩形的性质可得，再根据等腰三角形的三线合一可判断①；先根据等腰三角形的性质可得，再根据等腰直角三角形的判定与性质可得，然后根据角的和差即可判断②；先证出，从而可得，再设，从而可得，由此即可判断③；先证出，从而可得，再根据等腰三角形的定义可得为等腰三角形，然后根据角的和差可得，由此即可得判断④．
【详解】
解：四边形是矩形，
，
，
（等腰三角形的三线合一），则①正确；
，
，
又，
是等腰直角三角形，
，
，则②错误；
，
（等腰三角形的三线合一），
在和中，，
，
，
设，
，
，
，
，
，则③正确；
，
，
点是线段的中点，
，
在和中，，
，
，
为等腰三角形，
，
，即，
为等腰直角三角形，则④正确；
综上，判断正确的是①③④，
故答案为：①③④．

【点拨】本题考查矩形的性质、等腰三角形的判定与性质、三角形全等的判定定理与性质、勾股定理等知识点，较难的是④，正确找出两个全等三角形是解题关键．
21．或
【解析】
【分析】对是以为腰的等腰三角形分类讨论，当时，设，可得到，再根据折叠可得到，然后在Rt△ABE中利用勾股定理列方程计算即可；当时，过A作AH垂直于于点H，然后根据折叠可得到，在结合，利用互余性质可得到，然后证得△ABE≌△AHE，进而得到，然后再利用等腰三角形三线合一性质得到，然后在根据数量关系得到．
【详解】
解：当时，设，则，
∵沿翻折得，
∴，
在Rt△ABE中由勾股定理可得：即，
解得：；
当时，如图所示，过A作AH垂直于于点H，

∵AH⊥，，
∴，
∵，
∴，
∵沿翻折得，
∴，
∴，
在△ABE和△AHE中，
∴△ABE≌△AHE（AAS），
∴，
∴，
∴
∵，
∴，
∴，
综上所述，，
故答案为：
【点拨】本题主要考查等腰三角形性质，勾股定理和折叠性质，解题的关键是分类讨论等腰三角形的腰，然后结合勾股定理计算即可．
22．
【解析】
【分析】根据菱形性质，利用勾股定理求出AB的长度，再根据中位线定理求出OE的长即可．
【详解】
解：∵四边形是菱形，
∴，
∵，，
∴，
∴，
∵，O为AC中点，
∴，
故答案为：．
【点拨】本题主要考查菱形性质，勾股定理，中位线定理，熟练掌握以上知识点是解决本题的关键．
23．（1）证明见详解；（2）四边形ACDE是菱形，理由见详解．
【解析】
【分析】（1）利用平行四边形的性质，即可判定，即可得到，再根据CD∥AE，即可证得四边形ACDE是平行四边形；
（2）利用（1）的结论和平行四边形的性质可得AC=CD，由此即可判定是菱形．
【详解】
（1）证明：在ABCD中，AB∥CD，
∴，
∵点O为AD的中点，
∴，
在与中，
∵，
，
，
∴，
∴，
又∵BE∥CD ，
∴四边形ACDE是平行四边形；
（2）解：由（1）知四边形ACDE是平行四边形，，
∵，
∴，
∴四边形ACDE是菱形．

【点拨】本题考查了平行四边形的性质和判定、三角形全等、菱形的判定等，熟练掌握判定定理并融会贯通是解题的关键．
24．（1）证明过程见解析；（2）证明过程见解析．
【解析】
【分析】（1）根据矩形的性质可得AB=DC，∠B=∠DCF=90°，根据全等三角形的判定即可得到；
（2）根据矩形的性质可得AD∥BC，AD=BC，根据可得AD=EF，根据平行四边形的判定即可得到四边形AEFD是平行四边形．
【详解】
证明：（1）∵四边形ABCD是矩形，
∴AB=DC，∠B=∠DCB=90°，
∴∠DCF=90°，
在△ABE和△DCF中，
，
∴（SAS）．
（2）∵四边形ABCD是矩形，
∴AD∥BC，AD=BC，
即AD=BE+EC，
∵BE=CF，
∴AD=CF+EC，
即AD=EF，
∵点F在BC的延长线上，
∴AD∥EF，
∴四边形AEFD是平行四边形．
【点拨】本题考查了矩形的性质，全等三角形的判定，平行四边形的判定．熟记各个图形的性质和判定是解题的关键．
25．（1）；（2）菱形，见解析；（3）或
【解析】
【分析】（1）根据“直角三角形斜边上的中线等于斜边的一半”得；
（2）由题意可得，，由“直角三角形中角所对的直角边等于斜边的一半”，得，得，则四边形是平行四边形，再由折叠得，于是判断四边形是菱形；
（3）题中条件是“点是射线上一点”，因此又分两种情况，即点与点在直线的异侧或同侧，正确地画出图形即可求出结果．
【详解】
解：（1）如图①，在中，，
∵是斜边上的中线，，
∴．

（2）四边形是菱形．
理由如下：
如图②∵于点，
∴，
∴；
由折叠得，，
∵，
∴；
∵，，
∴，
∴，
∴，
∴四边形是平行四边形；
∵，
∴，
∴四边形是菱形．

（3）如图③，点与点在直线异侧，
∵，
∴；
由折叠得，，
∴；

如图④，点与点在直线同侧，
∵，
∴，
∴，
由折叠得，，
∴，
∴．
综上所述，或．

【点拨】此题主要考查了直角三角形的性质、轴对称的性质、平行四边形及特殊平行四边形的判定等知识与方法，在解第（3）题时，应进行分类讨论，解题的关键是准确地画出图形，以免丢解．
26．（1）；（2）①丙；②10
【解析】
【分析】（1）连接，则为等边三角形，即可求得既不相交也不平行的两条直线与所成角的大小；
（2）①根据正方体侧面展开图判断即可；
②根据对称关系作辅助线即可求得的最小值．
【详解】
解：（1）连接，


∵，与相交与点，
即既不相交也不平行的两条直线与所成角为，
根据正方体性质可得：，
∴为等边三角形，
∴，
即既不相交也不平行的两条直线与所成角为；
（2）①根据正方体展开图可以判断，
甲中与原图形中对应点位置不符，
乙图形不能拼成正方体，
故答案为丙；
②如图：作M关于直线AB的对称点，
连接，与交于点P，连接MP，
则，
过点N作BC垂线，并延长与交于点E，

∵点M到的距离是5，点N到的距离是3，
∴，
∵点M到的距离是2，点N到的距离是4，
∴，
∴，
故最小值为10．
【点拨】本题主要考查正方形的性质、正方体的侧面展开图、根据对称关系求最短距离、勾股定理等知识点，读懂题意，明确最小时的情况是解题的关键．
27．（1）见解析；（2）
【解析】
【分析】（1）证明△ABE≌△EHF，即可证明BE=CH；
（2）作FP⊥CD于P，求得PD=3−x，利用勾股定理即可求解．
【详解】
（1）证明：∵四边形ABCD是正方形，
∴∠ABE=90°，AB=BC，
∵∠AEF=90°，
∴∠AEB+∠FEH=90°．
而∠AEB+∠BAE=90°，
∴∠BAE=∠FEH．
又∵EF=AE，
∴△ABE≌△EHF．
∴BE=FH，AB=EH，
∴AB=BC=EH，则BC-EC=EH-EC，
∴BE=CH；
（2）作FP⊥CD于P，

由（1）可知EH=AB，
∴CE=3−x．
∴CH=FH=FP=x，
∴PD=3−x．
．
【点拨】本题考查了正方形的性质，全等三角形的性质和判定，勾股定理等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．
28．（1）见解析；（2）见解析；（3）∠DGO=α+45°或∠DGO=α-45°或∠DGO=45°-α．
【解析】
【分析】（1）四边形ABCD是正方形，，，又知道，可得到即可求解；
（2）作交AC于点H,则,知道四边形ABCD是正方形可得，推出，，，，，得到，，又知道得到即可求解
（3）分三种情况①点E在线段AB上、②点E在线段BA的延长线上、③点E在线段AB的延长线上，逐一进行讨论即可求解．
【详解】
解：（1）∵四边形ABCD是正方形，
∴，．
∴．
又∵，
∴．
∴．
（2）（解法一）作交AC于点H，如图1．则．

            图1
∵四边形ABCD是正方形，
∴，．
∴
∵，
∴．
∴．
∴．
∵，
∴．
又∵，
∴．
∴．
由（1）同理可得，
∴．
（解法二）作交AC于点H ，如图2．

            图2
∵四边形ABCD是正方形，
∴，．
∴，
∵，
∴．
∴．
∴．
又∵，
∴．
连接CE，FH ．
又∵．
∴四边形CEHF是平行四边形．
∴．
由（1）同理可得，
∴．
（3）解：①当点E在线段AB上时，

∵四边形ABCD是正方形，
∴∠BCD=∠ADC=90°，∠ACD=45°，
∵，
∴∠ADE=∠CDF，
∵∠ADE+∠EDC=∠ADC=90°，
∴∠EDC+∠CDF=90°，
即∠EDF=90°，
∵DE=DF，DG⊥EF，
∴∠GDF=∠2=45°，
∴∠1=45°-∠3，
∵∠BCD=90°，
∴∠3+∠2+∠CFE=90°，
∴∠3=90°-45°-α=45°-α，
∴∠1=45°-∠3=α，
∵∠DGO=∠ACD+∠1，
∴∠DGO=α+45°；
②当点E在线段BA的延长线上时，

∵四边形ABCD是正方形，
∴∠BCD=∠ADC=90°，∠BDC=45°，
∵，
∴∠ADE=∠CDF，
∵∠ADF+∠CDF=∠ADC=90°，
∴∠EDA+∠ADF=90°，
即∠EDF=90°，
∵DE=DF，DG⊥EF，
∴∠GDF=∠GFD=∠BDC=45°，
∴∠1=∠2，
∵∠BCD=90°，
∴∠3+∠2=90°，
∵∠3=∠CFE-∠GFD=α-45°，
∴∠2=90°-α+45°=135°-α，
∴∠1=∠2=135°-α，
∴∠DGO=90°-∠1=α-45°；
③当点E在线段AB的延长线上时，

∵四边形ABCD是正方形，
∴AB∥CD，∠ACD=45°，∠ABC=∠ADC=90°，
∵，
∴∠ADE=∠CDF，
∵∠ADE+∠EDC=∠ADC=90°，
∴∠EDC+∠CDF=90°，
即∠EDF=90°，
∴∠2=∠3，
∵DE=DF，DG⊥EF，
∴∠GDE=∠DEG=45°，
∴∠1+∠3=45°，
∵∠ABC=90°，
∴∠CFE+∠2+∠DEG=90°，
∵∠CFE-∠2=45°，
∴∠CFE=∠1=α，
∴∠DGO+∠1=∠ACD=45°，
∴∠DGO=45°-α．
综上：∠DGO=α+45°或∠DGO=α-45°或∠DGO=45°-α．
【点拨】本题属于四边形综合题，考查了正方形的性质，全等三角形的判定和性质，等腰直角三角形的判定和性质等知识，解题的关键是利用全等三角形的判定和性质得DE=DF，利用等腰直角三角形的性质求解．