广东省云浮市郁南县2022年八年级上学期期末数学试题解析版

这是一份广东省云浮市郁南县2022年八年级上学期期末数学试题解析版，共7页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
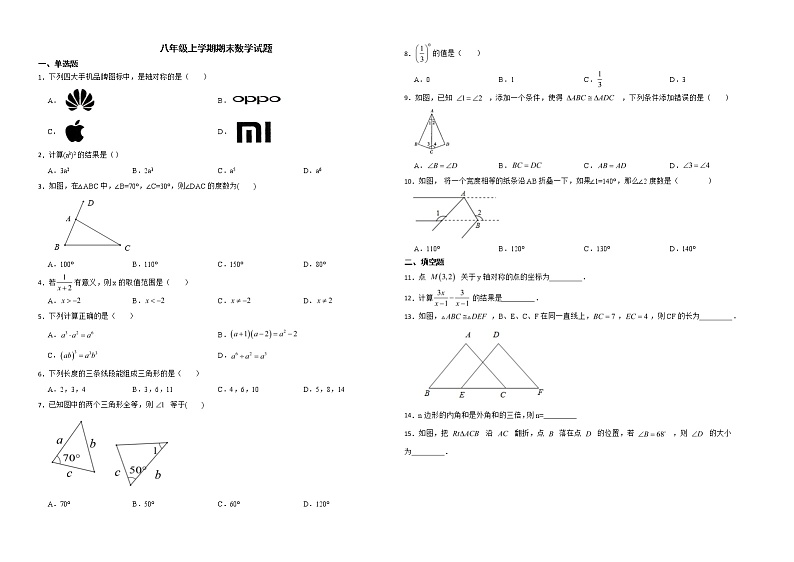
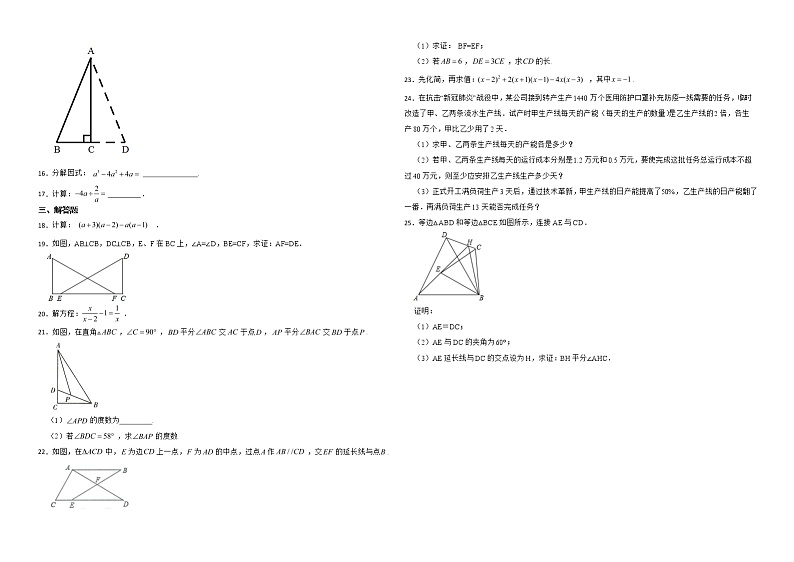
 八年级上学期期末数学试题一、单选题1．下列四大手机品牌图标中，是轴对称的是（　　）   A． B．C． D．2．计算(a3)2的结果是（）A．3a2 B．2a3 C．a5 D．a63．如图，在△ABC中，∠B=70°，∠C=30°，则∠DAC的度数为(　　)A．100° B．110° C．150° D．80°4．若有意义，则x的取值范围是（　　）A． B． C． D．5．下列计算正确的是（　　）A． B．C． D．6．下列长度的三条线段能组成三角形的是（　　）  A．2，3，4 B．3，6，11 C．4，6，10 D．5，8，147．已知图中的两个三角形全等，则 等于(　　)  A．70° B．50° C．60° D．120°8．的值是（　　）A．0 B．1 C． D．39．如图，已知 ，添加一个条件，使得 ，下列条件添加错误的是（　　）  A． B． C． D．10．如图， 将一个宽度相等的纸条沿AB折叠一下，如果∠1=140°，那么∠2度数是（        ）A．110° B．120° C．130° D．140°二、填空题11．点 关于y轴对称的点的坐标为　     　．   12．计算的结果是　     　．13．如图，，B、E、C、F在同一直线上，，，则CF的长为　     　．14．n边形的内角和是外角和的三倍，则n=　     　15．如图，把 沿 翻折，点 落在点 的位置，若 ，则 的大小为　     　．  16．分解因式： 　           　.   17．计算：　     　．三、解答题18．计算： ．   19．如图，AB⊥CB，DC⊥CB，E、F在BC上，∠A=∠D，BE=CF，求证：AF=DE．20．解方程：．21．如图，在直角，，平分交于点，平分交于点.（1）的度数为　     　.（2）若，求的度数.22．如图，在中，为边上一点，为的中点，过点作，交的延长线与点.（1）求证： BF=EF；（2）若，，求的长.23．先化简，再求值：，其中.24．在抗击“新冠肺炎”战役中，某公司接到转产生产1440万个医用防护口罩补充防疫一线需要的任务，临时改造了甲、乙两条流水生产线．试产时甲生产线每天的产能（每天的生产的数量）是乙生产线的2倍，各生产80万个，甲比乙少用了2天．（1）求甲、乙两条生产线每天的产能各是多少？   （2）若甲、乙两条生产线每天的运行成本分别是1.2万元和0.5万元，要使完成这批任务总运行成本不超过40万元，则至少应安排乙生产线生产多少天？   （3）正式开工满负荷生产3天后，通过技术革新，甲生产线的日产能提高了50%，乙生产线的日产能翻了一番．再满负荷生产13天能否完成任务？   25．等边△ABD和等边△BCE如图所示，连接AE与CD．证明：（1）AE＝DC；（2）AE与DC的夹角为60°；（3）AE延长线与DC的交点设为H，求证：BH平分∠AHC．
答案解析部分1．【答案】A【知识点】轴对称图形【解析】【解答】解：A、是轴对称图形，故此选项符合题意；B、不是轴对称图形，故此选项不符合题意；C、不是轴对称图形，故此选项不符合题意；D、不是轴对称图形，故此选项不符合题意；故答案为：A．【分析】根据轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．2．【答案】D【知识点】幂的乘方【解析】【分析】根据幂的乘方乘方法则：幂的乘方，底数不变指数相乘，即可求解．【解答】（a3)2=a3×2=a6．
故答案是：a6．【点评】本题主要考查了幂的乘方法则，正确理解法则：幂的乘方，底数不变指数相乘，是解题关键3．【答案】A【知识点】三角形的外角性质【解析】【解答】解：∵∠DAC是△ABC的一个外角，
∴∠DAC=∠B+∠C
∴∠DAC=70°+30°=100°.
故答案为：A.【分析】根据三角形的一个外角等于和它不相邻的两内角之和，即可求出∠DAC的度数。4．【答案】C【知识点】分式有意义的条件【解析】【解答】解：依题意得：x+2≠0，解得x≠-2，故答案为：C．【分析】分式有意义的条件：分母不为0，据此解答即可.5．【答案】C【知识点】同底数幂的乘法；同底数幂的除法；多项式乘多项式；积的乘方【解析】【解答】A、 ，故该选项不符合题意； B、 ，故该选项不符合题意；C、 ，故该选项符合题意；D、 ，故该选项不符合题意；故答案为：C．【分析】根据同底数幂的乘法及除法，多项式乘以多项式，积的乘方分别计算，再判断即可.6．【答案】A【知识点】三角形三边关系【解析】【解答】解：A、2+3＞4，能组成三角形；B、3+6＜11，不能组成三角形；C、4+6=10，不能组成三角形；D、5+8＜14，不能够组成三角形．故答案为：A．【分析】根据三角形三边的关系，三角形任意两边之和大于第三边，任意两边之差小于第三边。即可判断四个选项中符合题意的选项。7．【答案】C【知识点】三角形全等及其性质【解析】【解答】解：∵两个三角形全等，∴第二个三角形没有标注的边为a，且a和c的夹角为70°∴∠1=180°－70°－50°=60°故答案为：C．【分析】根据全等三角形的对应边相等和全等三角形的对应角相等，可得第二个三角形没有标注的边为a，且a和c的夹角为70°，利用三角形的内角和定理即可求出∠1．8．【答案】B【知识点】0指数幂的运算性质【解析】【解答】∵ ， 故答案为：B．【分析】根据a0=1(a≠0）计算即可.9．【答案】B【知识点】三角形全等的判定【解析】【解答】若添加 ，则可根据“AAS”判定两三角形全等； 若添加 ，则有两组对应边相等，但相等的角不是夹角，不能判定两三角形全等；若添加 ，则可根据“SAS”判定两三角形全等；若添加 ，则可根据“ASA”判定两三角形全等；故答案为：B【分析】根据三角形全等的判定定理添加条件即可．10．【答案】A【知识点】平行线的性质；翻折变换（折叠问题）【解析】【解答】解：如图，∵将一个宽度相等的纸条沿AB折叠，∴∠3=∠4，∵a∥b，∴∠1=∠3+∠4，∠2+∠3=180°，∴2∠3=140°，∴∠3=70°，∴∠2=180°-70°=110°．故答案为：A．【分析】由折叠的性质可得∠3=∠4，由平行线的性质可得∠1=∠3+∠4，∠2+∠3=180°，从而求出∠3的度数，继而得出∠2的度数.11．【答案】(-3,2)【知识点】关于坐标轴对称的点的坐标特征【解析】【解答】保持纵坐标不变，横坐标取相反数故点 关于y轴对称的点的坐标为(-3,2)故答案为：(-3,2)．【分析】根据关于y轴对称的点的坐标的特点求解即可．12．【答案】3【知识点】分式的加减法【解析】【解答】 ， 故答案为：3．【分析】根据同分母分式分式的减法法则进行计算，再约分即可.13．【答案】3【知识点】三角形全等及其性质【解析】【解答】∵△ABC≌△DEF，∴ BC=EF，∵ BC=7，EC=4，∴ CF=7-4=3，故答案为：3．【分析】根据全等三角形的对应边相等可得BC=EF，利用CF=BC-EC即可求解.14．【答案】8【知识点】多边形内角与外角【解析】【解答】解：n边形的内角和为：(n−2)×180°，n边形的外角和为：360°，根据题意得：(−2)×180°=3×360°，解得：n=8，故答案为：8．【分析】由于n边形的内角和为：(n−2)×180°，n边形的外角和为：360°，根据题意列出方程并解之即可.15．【答案】【知识点】翻折变换（折叠问题）【解析】【解答】根据翻折变换的特点可知：故答案为： ．【分析】根据折叠前后图形全等，对应边、对应角相等，据此解答即可.16．【答案】 ；【知识点】提公因式法与公式法的综合运用【解析】【解答】 =a(a2-4a+4)=a(a-2)2.故答案是：a(a-2)2.【分析】先提取公因式a，然后利用完全平方公式进行分解即可.17．【答案】【知识点】分式的乘除法【解析】【解答】解：；
【分析】先将除法转化为乘法，再约分即可.18．【答案】解： =  = ．【知识点】整式的混合运算【解析】【分析】直接利用多项式乘多项式以及单项式乘多项式，再合并同类项得出答案．19．【答案】证明：∵AB⊥CB，DC⊥CB，  ∴∠B=∠C=90°，∵BE=CF ∴BF=CE，且∠A=∠D，∠B=∠C=90°，∴△ABF≌△DCE（AAS）∴AF=DE.【知识点】三角形全等及其性质；三角形全等的判定（AAS）【解析】【分析】由题意可得∠B=∠C=90°，BF=CE，由“AAS”可证△ABF≌△DCE，可得AF=DE．20．【答案】解：两边同时乘以得：解得：经检验，是原方程的解，所以原方程的解是；【知识点】解分式方程【解析】【分析】利用去分母将分式方程化为整式方程，解出整式方程并检验即得.21．【答案】（1）45°（2）解：∵，∴．∵平分，∴．【知识点】三角形内角和定理；三角形的外角性质；角平分线的定义【解析】【解答】(1)∵，∴∠BAC+∠ABC=90°，∵平分，平分，∴∠PAB+∠PBA=（∠BAC+∠ABC）=45°，∴=∠PAB+∠PBA=；【分析】根据三角形的内角和求出∠BAC+∠ABC=90°，由角平分线的定义可得∠PAB+∠PBA=（∠BAC+∠ABC）=45°，利用三角形外角的性质可得=∠PAB+∠PBA=.22．【答案】（1）证明：∵AB//CD，∴∠DAB=∠ADE∵为的中点，∴AF=DF，在△AFB和△DFE中，∴∴△AFB≌△DFE，∴BF=EF．（2）解：∵△AFB≌△DFE，∴DE=AB，∵，，∴CE=2，∴CD=8.【知识点】平行线的性质；三角形全等的判定（AAS）【解析】【分析】（1）由平行线的性质可得∠DAB=∠ADE，由线段的中点可得AF=DF，根据AAS证明△AFB≌△DFE，可得BF=EF；
（2） 由△AFB≌△DFE可得DE=AB，从而求出CE=2，利用CD=CE+DE即可求解.23．【答案】解：原式当时， 原式【知识点】利用整式的混合运算化简求值【解析】【分析】利用整式的混合运算将原式化简，再将x值代入计算即可.24．【答案】（1）解：设乙条生产线每天的产能是x万个，则甲条生产线每天的产能是2x万个，依题意有  ﹣ ＝2，解得x＝20，经检验，x＝20是原方程的解，2x＝2×20＝40，故甲条生产线每天的产能是40万个，乙条生产线每天的产能是20万个；（2）解：设安排乙生产线生产y天，依题意有  0.5y+1.2× ≤40，解得y≥32．故至少应安排乙生产线生产32天；（3）解：（40+20）×3+[40×（1+50%）+20×2]×13  ＝180+1300＝1480（万个），1440万个＜1480万个，故再满负荷生产13天能完成任务．【知识点】分式方程的实际应用；一元一次不等式的应用【解析】【分析】（1）设乙条生产线每天的产能是x万个，则甲条生产线每天的产能是2x万个，根据题意列出方程即求解可；（2）设安排乙生产线生产y天，再根据完成这批任务总运行成本不超过40万元列出不等式求解即可；（3）根据题意求出原来满负荷生产3天和再满负荷生产13天的产能的和，然后与1440万相比即可解答．25．【答案】（1）证明：∵△ABD和△BCE都是等边三角形，∴AB＝DB，EB＝CB，∠ABD＝∠EBC∴∠ABE＝∠DBC∴在△ABE和△DBC中∴△ABE≌△DBC（SAS）∴AE＝DC；（2）证明：∵△ABE≌△DBC∴∠BAE＝∠BDC又∵∠BAE+∠HAD+∠ADB＝120°∴∠BDC+∠HAD+∠ADB＝120°∴△ADH中，∠AHD＝180°﹣120°＝60°即AE与DC的夹角为60°；（3）证明：过B作BF⊥DC于F，BG⊥AH于G，如图：∵△ABE≌△DBC∴S△ABE＝S△DBC，即AE×BGDC×BF∵AE＝DC∴BG＝BF∵BF⊥DC于F，BG⊥AH于G∴BH平分∠AHC．【知识点】三角形的面积；三角形内角和定理；等边三角形的性质；角平分线的判定；三角形全等的判定（SAS）【解析】【分析】（1）证明△ABE≌△DBC（SAS）可得AE＝DC；
（2） 由（1）知△ABE≌△DBC，可得∠BAE＝∠BDC， 从而求出∠BDC+∠HAD+∠ADB=∠BAE+∠HAD+∠ADB＝120° ，利用三角形的内角和即可求解；
（3） 过B作BF⊥DC于F，BG⊥AH于G，如图，由△ABE≌△DBC，可得S△ABE＝S△DBC，即AE×BGDC×BF，由AE＝DC可得BG＝BF，根据角平分线的判定定理即证.