第02讲+玩转立体几何中的角度、体积、距离问题-【暑假自学课】新高二数学暑假精品课（苏教版2019选择性必修第一册）

第02讲 玩转立体几何中的角度、体积、距离问题

【学习目标】

1.掌握各种角的定义，弄清异面直线所成的角与两直线所成的角，二面角与二面角的平面角，直线与平面所成的角和斜线与平面所成的角，二面角与两平面所成的角的联系与区别，弄清他们各自的取值范围。

2.细心体会求空间角的转化和数形结合思想。

3.掌握各种距离和距离的求解方法.

【基础知识】

知识点1.求点线、点面、线面距离的方法

 (1)若P是平面外一点，a是平面内的一条直线，过P作平面的垂线PO，O为垂足，过O作OA⊥a，连接PA，则以PA⊥a．则线段PA的长即为P点到直线a的距离(如图所示)．

 (2)一条直线与一个平面平行时，这条直线上任意一点到这个平面的距离叫直线与平面的距离．

 (3)求点面距离的常用方法：①直接过点作面的垂线，求垂线段的长，通常要借助于某个直角三角形来求解．

 ②转移法：借助线面平行将点转移到直线上某一特殊点到平面的距离来求解．

 ③体积法：利用三棱锥的特征转换位置来求解．

知识点2.异面直线所成角的常用方法

求异面直线所成角的一般步骤：

 (1)找(或作出)异面直线所成的角——用平移法，若题设中有中点，常考虑中位线.

 (2)求——转化为求一个三角形的内角，通过解三角形，求出所找的角.

(3)结论——设(2)所求角大小为θ.若，则θ即为所求；若，则即为所求.

知识点3.直线与平面所成角的常用方法

求平面的斜线与平面所成的角的一般步骤

(1)确定斜线与平面的交点(斜足)；

(2)通过斜线上除斜足以外的某一点作平面的垂线，连接垂足和斜足即为斜线在平面上的射影，则斜线和射影所成的锐角即为所求的角；

(3)求解由斜线、垂线、射影构成的直角三角形.

知识点4.作二面角的三种常用方法

(1)定义法：在二面角的棱上找一个特殊点，在两个半平面内分别作垂直于棱的射线.如图①，则∠AOB为二面角α-l-β的平面角.

(2)垂直法：过棱上一点作棱的垂直平面，该平面与二面角的两个半平面产生交线，这两条交线所成的角，即为二面角的平面角.如图②，∠AOB为二面角α-l-β的平面角.

(3)垂线法：过二面角的一个面内异于棱上的一点A向另一个平面作垂线，垂足为B，由点B向二面角的棱作垂线，垂足为O，连接AO，则为二面角的平面角或其补角.如图③，为二面角的平面角.

知识点5.求体积的常用方法

选择合适的底面，再利用体积公式求解.

【考点剖析】

考点一：异面直线所成的角

例1．在空间四边形中，E，F，G，H分别是，，，的中点，若，且与所成的角为60°，则的长为（       ）

A．1或 B．或 C．1或 D．或

考点二：线面角

例2．如图，在三棱柱中，底面是正三角形，底面，且，，则直线与平面所成角的正弦值为______．

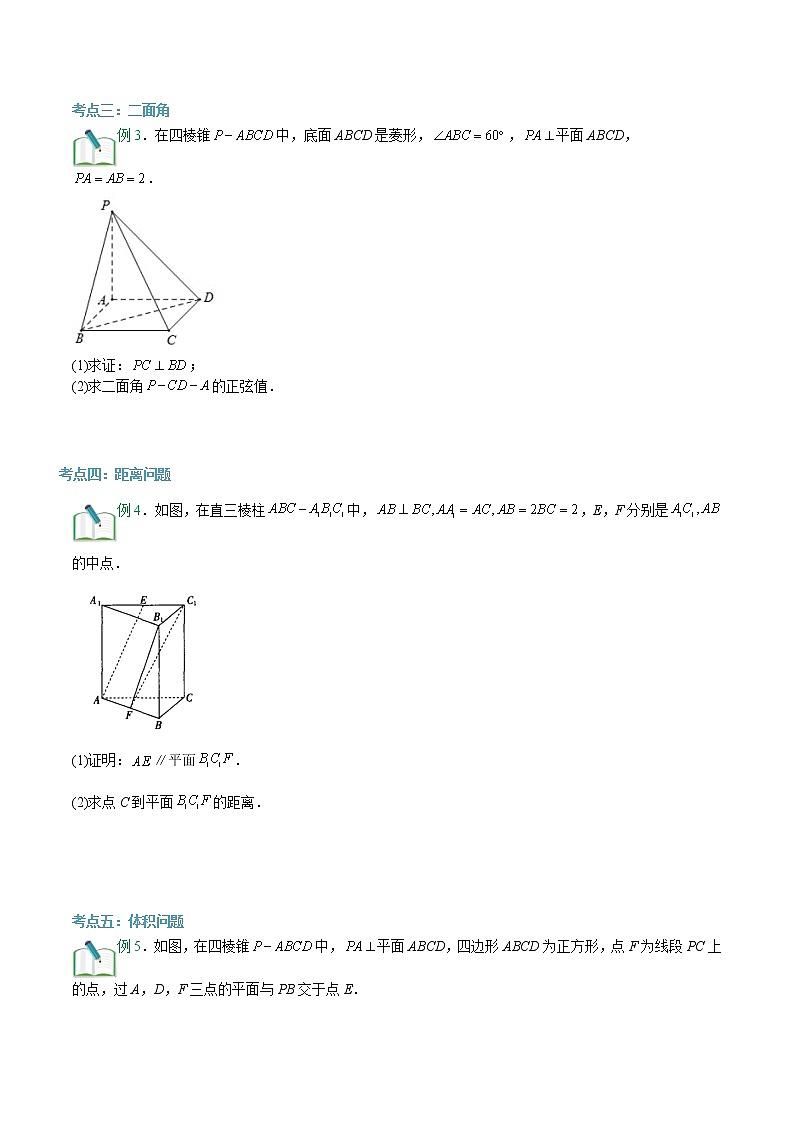
考点三：二面角

例3．在四棱锥中，底面ABCD是菱形，，平面ABCD，．

(1)求证：；

(2)求二面角的正弦值．

考点四：距离问题

例4．如图，在直三棱柱中，，E，F分别是的中点．

(1)证明：∥平面．

(2)求点C到平面的距离．

考点五：体积问题

例5．如图，在四棱锥中，平面ABCD，四边形ABCD为正方形，点F为线段PC上的点，过A，D，F三点的平面与PB交于点E．

(1)证明：平面ABCD；

(2)若E为PB中点，且，求四棱锥的体积．

【真题演练】

1．在正方体中，P为的中点，则直线与所成的角为（       ）

A． B． C． D．

2．如图，四棱锥S-ABCD的底面为正方形，SD⊥底面ABCD，则下列结论中不正确的是（ ）

A．AC⊥SB

B．AB∥平面SCD

C．SA与平面SBD所成的角等于SC与平面SBD所成的角

D．AB与SC所成的角等于DC与SA所成的角

1．线面平行垂直的判定；2．线面角，异面直线所成角

3．已知四棱锥的底面是正方形，侧棱长均相等，是线段上的点（不含端点），设与所成的角为，与平面所成的角为，二面角的平面角为，则

A． B． C． D．

4．在正方体中，为棱的中点，则异面直线与所成角的正切值为

A． B． C． D．

5．已知正方体中，、分别为的中点，那么异面直线与所成角的余弦值为____________.

6．如下图，在四棱锥中，底面是正方形，平面平面，，．

（1）求与所成角的余弦值；

（2）求证：．

7．如图，三角形所在的平面与长方形所在的平面垂直，，，．

（1）证明：平面；

（2）证明：；

（3）求点到平面的距离．

8．如图，在圆锥中，已知，圆的直径，点在上，且，为的中点．

（I）证明：平面；

（II）求直线OC和平面所成角的正弦值．

9．如图，P是边长为1的正六边形ABCDEF所在平面外一点，，P在平面ABC内的射影为BF的中点O．

（Ⅰ）证明⊥；

（Ⅱ）求面与面所成二面角的大小的余弦值．

10．在四棱锥中，底面ABCD为正方形，平面平面ABCD，点M在线段PB上，平面MAC，.

(1)判断M点在PB的位置并说明理由；

(2)记直线DM与平面PAC的交点为K，求的值；

(3)若异面直线CM与AP所成角的余弦值为，求二面角的平面角的正切值.

11．如图，在长方体中，AD=1，，H，F分别是棱，的中点.

(1)判断直线HF与平面的位置关系，并证明你的结论；

(2)求直线HF与平面ABCD所成角的正弦值；

(3)在线段HF上是否存在一点Q，使得点Q到平面的距离是，若存在，求出的值；若不存在，说明理由.

【过关检测】

1．在长方体中，，，点、分别是棱、的中点，、、平面，直线平面，则直线与直线所成角的余弦值为（       ）

A． B． C． D．

2．在正方体中，E，F分别为棱AD，的中点，则异面直线EF与夹角的余弦值为（       ）

A． B． C． D．

3．如图所示，三棱锥的底面ABC是等腰直角三角形，，且，，则PC与平面PAB所成角的余弦值等于（       ）

A． B． C． D．

4．在空间四边形中，E，F，G，H分别是，，，的中点，若，且与所成的角为60°，则的长为（       ）

A．1或 B．或 C．1或 D．或

5．在棱长为1的正方体中，O为正方形的中心，则下列结论错误的是（       ）

A．

B．∥平面

C．点B到平面的距离为

D．直线与直线的夹角为

6．在正方体中，分别为的中点，则下列结论中正确的是（       ）

A．

B．二面角的正切值为

C．异面直线与所成角的余弦值为

D．点到平面的距离是点到平面的距离的2倍

7．如图，是半球的直径，为球心，依次是半圆上的两个三等分点，是半球面上一点，且，

(1)证明：平面平面；

(2)若点在底面圆内的射影恰在上，求二面角的余弦值．

8．已知平面四边形，，，，现将沿边折起，使得平面平面，此时，点为线段的中点.

(1)求证：平面；

(2)若为的中点，求与平面所成角的正弦值；

(3)在（2）的条件下，求二面角的平面角的余弦值.

9．已知四棱锥的底面是边长为2的菱形，底面.

(1)求证：平面；

(2)当，时，求直线与所成角的余弦值；

10．已知四棱锥的底面是边长为2的菱形，底面．

(1)求证：平面；

(2)已知，

（ⅰ）当时，求直线与所成角的余弦值；

（ⅱ）当直线与平面所成的角为时，求四棱锥的体积．

11．在直三棱柱中，，，.

(1)求异面直线与所成角正切值的大小；

(2)求点与平面的距离.