2022北京四中初三（上）期中数学（无答案）

这是一份2022北京四中初三（上）期中数学（无答案），共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本题共16分，每小题2分）
第1-8题均有四个选项，符合题意的选项只有一个.
1.下列四个图形中，是中心对称图形的是（ ）.
A.B.C.D.
2.抛物线的顶点坐标是（ ）.
A.B.C.D.
3.如图，是的外接圆，，则的度数为（ ）.
A.30°B.50°C.80°D.100°
4.下列方程中，有两个相等的实数根的方程是（ ）.
A.B.
C.D.
5.将抛物线先向右平移2个单位，再向上平移1个单位，得到的新抛物线的表达式为（ ）.
A.B.
C.D.
6.如图，绕点逆时针旋转75°，得到，若，则等于（ ）.
A.115°B.75°C.40°D.35°
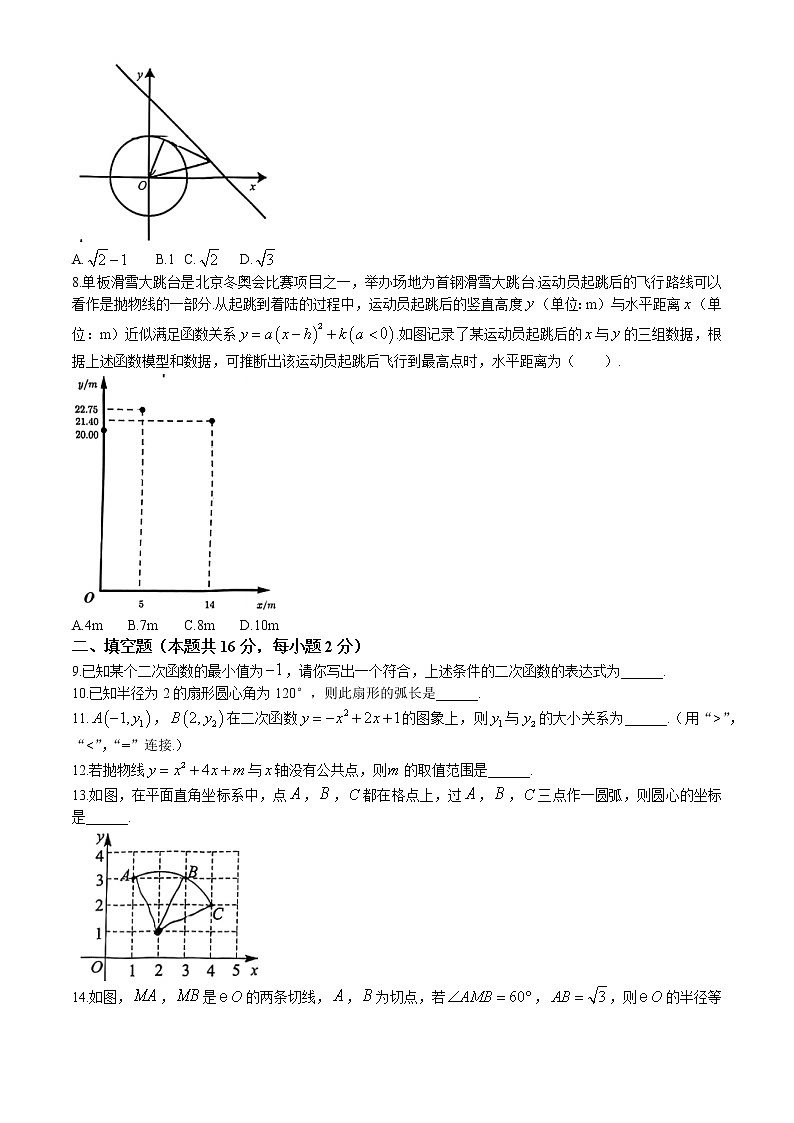
7.如图，的半径是1，点是直线上一动点，过点作的切线，切点为，连接，，则的最小值为（ ）.
A.B.1C.D.
8.单板滑雪大跳台是北京冬奥会比赛项目之一，举办场地为首钢滑雪大跳台.运动员起跳后的飞行路线可以看作是抛物线的一部分.从起跳到着陆的过程中，运动员起跳后的竖直高度（单位：m）与水平距离（单位：m）近似满足函数关系.如图记录了某运动员起跳后的与的三组数据，根据上述函数模型和数据，可推断出该运动员起跳后飞行到最高点时，水平距离为（ ）.
A.4mB.7mC.8mD.10m
二、填空题（本题共16分，每小题2分）
9.已知某个二次函数的最小值为，请你写出一个符合，上述条件的二次函数的表达式为______.
10.已知半径为2的扇形圆心角为120°，则此扇形的弧长是______.
11.，在二次函数的图象上，则与的大小关系为______.（用“>”，“<”，“=”连接.）
12.若抛物线与轴没有公共点，则的取值范围是______.
13.如图，在平面直角坐标系中，点，，都在格点上，过，，三点作一圆弧，则圆心的坐标是______.
14.如图，，是的两条切线，，为切点，若，，则的半径等于______.
15.为响应国家号召打赢脱贫攻坚战，小明利用信息技术开了一家网络商店，将家乡的土特产销往全国.今年6月份盈利12000元，8月份盈利27000元，求6月份到8月份盈利的月平均增长率.设6月份到8月份盈利的月平均增长率为，根据题意，可列方程为______.
16.已知二次函数的对称轴为直线，它的图象经过点，，.对于下列四个结论：
①；
②；
③方程的解为，；
④对于任意实数，总有.
其中正确的结论是______.（填写序号）.
三、解答题（本题共68分）
解答应写出文字说明、演算步骤或证明过程.
17.（6分）解下列方程：
（1）；（2）.
18.（5分）下面是“过圆外一点作圆的切线”的尺规作图过程.
（1）请根据上述作法完成尺规作图；
（2）连接，，可证，理由是________________________；
（3）直线，是的切线，依据是________________________.
19.（5分）已知二次函数：.
（1）将化成的形式；
（2）在右图中画出二次函数的图象；
（3）当时，利用图象直接写出的取值范围.
20.（5分）如图，在平面直角坐标系中，，，.
（1）将先向右平移5个单位长度，再向下平移2个单位长度，得到，请在图中画出；
（2）将绕点顺时针旋转90°得到，请在图中画出；
（3）连接，线段的长等于______.
21.（5分）已知关于的方程.
（1）求证：此方程总有实数根；
（2）若为整数，且此方程有两个不相等的整数根，求的值.
22.（5分）如图，是的直径，是弦，且于点，，.求的半径.
23.（5分）如图，有一农户要建一个矩形菜地，菜地的一边利用长为12m的墙（），另外三边用26m长的篱笆围成.求当矩形的边长为多少m时，菜地面积为？
24.（6分）如图，是的直径，点为上一点，平分，交于点，交于点，延长到点，使得.
（1）求证：与相切；
（2）若的半径5，，求的长.
25.（6分）已知函数的图象过点，.
（1）直接写出的解析式；
（2）如图，请补全分段函数的图象（不要求列表）.
并回答以下问题：
①写出此分段函数的一条性质：________________________；
②若此分段函数的图象与直线有三个公共点，请结合函数图象直接写出实数的取值范围；
（3）横、纵坐标都是整数的点叫做整点，记（2）中函数的图象与直线围成的封闭区域（不含边界）为“区域”，请直接写出区域内所有整点的坐标.
26.（6分）已知，抛物线：经过点，.
（1）求抛物线的对称轴；
（2）平移抛物线：，使其顶点在直线上，设平移后的抛物线的顶点的横坐标为.求抛物线与轴交点的纵坐标的最大值.
（3）在（2）的条件下，抛物线与轴交于点，将其向左平移2个单位得到点，若抛物线与线段只有1个公共点，直接写出的取值范围.
27.（7分）如图，在正方形中，点在线段的延长线上，连接，并将线段绕点顺时针旋转90°，得到线段，连接，，，线段与线段相交于点.
（1）依据题意完成作图，请写出的度数，并给出证明；
（2）求证：点是线段的中点；
（3）直接写出线段，和的数量关系.
28.（7分）在平面直角坐标系中，已知点和，对于点定义如下：以点为对称中心作点的对称点，再将对称点绕点逆时针旋转90°，得到点，称点为点的反转点.
已知的半径为1.
（1）如图，点，，点在上，点为点的反转点.
①当点的坐标为时，在图中画出点；
②当点在上运动时，求线段长的最大值；
（2）已知点是上一点，点和是外两个点，点为点的反转点.若点在第一象限内，点在第四象限内，当点在上运动时，直接写出线段长的最大值和最小值的差.已知：和外一点.
求作：过点的的切线.
作法：如图，
①连接；
②分别以点和点为圆心，大于的长为半径作弧，两弧相交于，两点；
③作直线，交于点；
④以点为圆心，的长为半径作圆，交于，两点；
⑤作直线，.
直线，即为所求作的切线.