华师大版第4章 图形的初步认识综合与测试单元测试达标测试

这是一份华师大版第4章 图形的初步认识综合与测试单元测试达标测试，共9页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
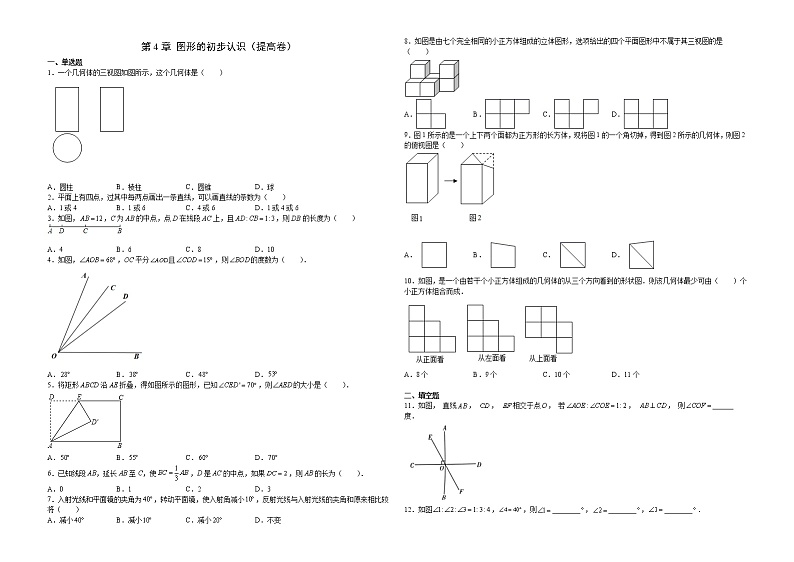
第4章 图形的初步认识（提高卷）一、单选题1．一个几何体的三视图如图所示，这个几何体是（　　）
 A．圆柱 B．棱柱 C．圆锥 D．球2．平面上有四点，过其中每两点画出一条直线，可以画直线的条数为（    ）A．1或4 B．1或6 C．4或6 D．1或4或63．如图，，C为AB的中点，点D在线段AC上，且，则DB的长度为（    ）
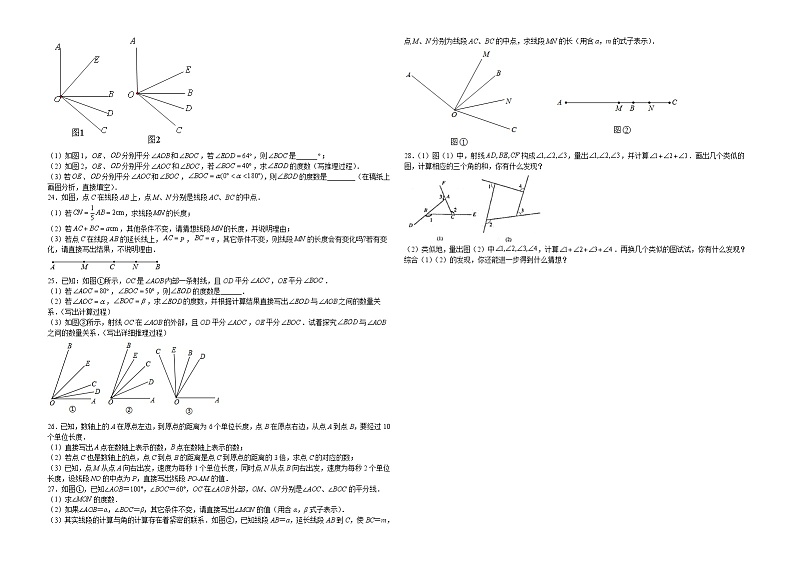
 A．4 B．6 C．8 D．104．如图，，OC平分且，则的度数为（    ）．A． B． C． D．5．将矩形ABCD沿AE折叠，得如图所示的图形，已知，则的大小是（    ）．A． B． C． D．6．已知线段AB，延长AB至C，使，D是AC的中点，如果，则AB的长为（    ）．A．0 B．1 C．2 D．37．入射光线和平面镜的夹角为，转动平面镜，使入射角减小，反射光线与入射光线的夹角和原来相比较将（    ）A．减小 B．减小 C．减小 D．不变8．如图是由七个完全相同的小正方体组成的立体图形，选项给出的四个平面图形中不属于其三视图的是（    ）A． B． C． D．9．图1所示的是一个上下两个面都为正方形的长方体，现将图1的一个角切掉，得到图2所示的几何体，则图2的俯视图是（    ） A．  B．  C．  D． 10．如图，是一个由若干个小正方体组成的几何体的从三个方向看到的形状图．则该几何体最少可由（　　）个小正方体组合而成．A．8个 B．9个 C．10个 D．11个 二、填空题11．如图， 直线， ， 相交于点， 若， ， 则______度．12．如图，，则________，________，________．13．如果两个角的两边分别垂直，其中一个角比另一个角的2倍少，那么这两个角的和是__________．14．如图，已知点C为AB上一点，AC＝12cm，CB＝AC，D、E分别为AC、AB的中点；则DE的长为_____cm．15．直线，垂足为点，直线经过点，若锐角，则__________（用含的代数式表示）.16．如图1，线段OP表示一条拉直的细线，A、B两点在线段OP上，且OA：AP＝2：3，OB：BP＝3：7．若先固定A点，将OA折向AP，使得OA重叠在AP上；如图2，再从图2的B点及与B点重叠处一起剪开，使得细线分成三段，则此三段细线由小到大的长度比是 ________．17．已知，，将一副三角板按照如图方式摆放在平行线之间，且线段BC落在直线MN上，线段DE落在直线PQ上，其中，，CO平分，EO平分，两条角平分线相交与点O，则________．18．如图，点E，F分别在长方形的边，上，连接．将长方形沿对折，点A落在处；将对折，点D落在的延长线上的处，得到折痕．若，则________°．19．如图1，点C在线段AB上，图中共有三条线段AB，AC和BC，若其中有一条线段的长度是另外一条线段长度的2倍，则称点C是线段AB的“巧点”．（1）线段的中点__这条线段的“巧点”；（填“是”或“不是”）；（2）如图2，已知AB＝15cm．动点P从点A出发，以2cm/s的速度沿AB向点B匀速运动；点Q从点B出发，以1cm/s的速度沿BA向点A匀速运动，点P，Q同时出发，当其中一点到达终点时，运动停止．设移动的时间为t（s），当t＝__s时，Q为A，P的“巧点”．20．如图，为直线上一点，过点作射线，，将一直角三角板（）的直角顶点放在点处，一边在射线上，另一边与都在直线的上方．将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周．经过______秒后，恰好评分；若三角板在转动的同时，射线也绕点以每秒5°的速度沿顺时针方向旋转一周，如图，那么经过______秒，平分？三、解答题21．如图，数轴上点B表示的数为﹣4，点A表示的数为10．（1）求A、B两点间的距离；（2）若动点P、Q分别以每秒8个单位长度和每秒4个单位长度的速度从点A、B同时出发沿数轴向负方向作匀速运动，当点P的运动时间为t秒时，①写出点P、Q所表示的数；（用含t的代数式表示）②若数轴上的点M到点P和点Q的距离相等，求的值．22．已知C，D是线段AB上两点，，D为AB的中点．（1）如图1，若，求线段CD的长；（2）如图2，若E为AC的中点，．①求AE：AB的值；②求线段AB的长．23．已知，（1）如图1，、分别平分和，若，则是______；（2）如图2，、分别平分和，若，求的度数（写推理过程）．（3）若、分别平分和，，则的度数是________（在稿纸上画图分析，直接填空）．24．如图，点C在线段AB上，点M、N分别是线段AC、BC的中点．（1）若，求线段的长度；（2）若，其他条件不变，请猜想线段的长度，并说明理由；（3）若点C在线段AB的延长线上，，，其它条件不变，则线段MN的长度会有变化吗?若有变化，请直接写出结果，不说明理由．25．已知：如图①所示，OC是内部一条射线，且OD平分，OE平分．（1）若，，则的度数是______．（2）若，，求的度数，并根据计算结果直接写出与之间的数量关系．（写出计算过程）（3）如图③所示，射线OC在的外部，且OD平分，OE平分．试着探究与之间的数量关系．（写出详细推理过程）26．已知，数轴上的A在原点左边，到原点的距离为6个单位长度，点B在原点右边，从点A到点B，要经过10个单位长度．（1）直接写出A点在数轴上表示的数，B点在数轴上表示的数；（2）若点C也是数轴上的点，点C到点B的距离是点C到原点的距离的3倍，求点C的对应的数；（3）已知，点M从点A向右出发，速度为每秒1个单位长度，同时点N从点B向右出发，速度为每秒2个单位长度，设线段NO的中点为P，直接写出线段PO-AM的值．27．如图①，已知∠AOB＝100°，∠BOC＝60°，OC在∠AOB外部，OM、ON分别是∠AOC、∠BOC的平分线．（1）求∠MON的度数．（2）如果∠AOB＝α，∠BOC＝β，其它条件不变，请直接写出∠MON的值（用含α，β式子表示）．（3）其实线段的计算与角的计算存在着紧密的联系．如图②，已知线段AB＝a，延长线段AB到C，使BC＝m，点M、N分别为线段AC、BC的中点，求线段MN的长（用含a，m的式子表示）．28．（1）图（1）中，射线构成，量出，并计算．画出几个类似的图，计算相应的三个角的和，你有什么发现？（2）类似地，量出图（2）中，计算．再换几个类似的图试试，你有什么发现？综合（1）（2）的发现，你还能进一步得到什么猜想？
第4章 图形的初步认识（提高卷）1．A2．D3．D．4．B．5．B．6．D．7．C．8．C．9·C．10．B．11．120．12．40；120；160．13．或．14．4．15．【答案】【详解】解：由题意，需讨论一下两种情况：如图1，∵AB⊥CD，
∴∠AOC＝90°．
∴∠AOF＝180°−∠AOC−∠COE＝180°−90°−m°＝90°−m°．
②如图2．∵AB⊥CD，
∴∠AOD＝90°．
∵∠COE与∠DOF是对顶角，
∴∠COE＝∠DOF＝m°．
∴∠AOF＝∠AOD＋∠DOF＝90°＋m°．
综上：∠AOF＝．
故答案为：．16．【详解】解：设OP=10k，则OA=4k，AP=6k，OB=3k，BP=7k，∴AB=1k，BO=3k，从图2的B点及与B点重叠处一起剪开后，细线分成三段为：2AB=2k，BO=3k，BP=5k，∴三段细线由小到大的长度比是2AB：BO：BP=2：3：5．故答案为：2：3：5．17．【详解】延长CO交PQ于点F，则∠COE=∠CFE+∠OEF，∵，，CO平分，EO平分，∴∠BCF=30°，∠OEF=22.5°，∵，∴∠BCF=∠CFE，∴∠COE=30°+22.5°=52.5°，故答案为：52.5°．18．【详解】解：由翻折的性质可知：∠BEA＝∠BEA′＝70°，∠DEF＝∠FED′，∴∠BEF＝∠BEA′＋∠FED′＝∠AEA′＋∠DED′＝×180°＝90°．∴∠FED′＝90°−∠BEA′＝90°−70°＝20°．故答案为：20．19．解：（1）若线段中点为C点，AB＝2AC，所以中点是这条线段“巧点”（2）设A点为数轴原点，作数轴，设运动时间为t秒；t最大＝7.5，A：0，P：0+2t＝2t，Q：15﹣t，①Q为AP中点，，∴t＝7.5；②AQ＝2PQ，AQ＝15﹣t﹣0＝15﹣t，PQ＝2t﹣（15﹣t）＝3t﹣15，∵AQ＝2PQ，∴15﹣t＝2（3t﹣15），∴；③PQ＝2AQ，得3t﹣15＝2（15﹣t），∴t＝97.5（舍去）．综上所述：t＝7.5或．故答案为：（1）是；（2）7.5或．20．解：①如图2中，∵∠AOC=30°，∴∠BOC=180°∠AOC=150°，∵OM平分∠BOC，∴∠COM=∠BOM=∠BOC=75°，∠AON=180°90°75°=15°，∴s，故答案为：5；②根据题意，如图：OC平分∠MON；∵∠MON=90°，∴∠NOC=45°，∴，∵三角板绕点O以每秒3°的速度，射线OC也绕O点以每秒5°的速度旋转，设∠AON为3t，∠AOC为30°+5t，∴，解得：，∴那么经过7.5秒，平分．故答案为：7.5．21．解：（1）由题意得：A、B两点间的距离为10-（-4）=14；（2）①由题意得：，∴点P表示的数为，点Q表示的数为；②当点P和点Q重合时，则有，解得：，由①可知：，∵数轴上的点M到点P和点Q的距离相等，∴点M是线段PQ的中点，则可分：当点P在点Q的右边时，则，（），∴，∴，，∴；当点P在点Q的左边时，则，（），∴，∴，，∴，∴综上所述：的值为．22．解：（1）∵，∴，∵，∴，∴，∴，∵D为AB的中点，∴，∴；（2）①∵E为AC的中点，∴，∵，∴，∵，∴，∴，∴；②∵D是AB的中点，∴，∵，∴，∴．23．解：（1）∵，OE平分，∴，∵，∴，∵OD平分，∴，故答案为：38；（2）∵OD平分，，，∴，，∵OE平分，∴，∴；（3）如图3所示，当OE，OD都在∠AOB外部时，∵OE，OD分别平分∠AOC，∠BOC，∴，，∴，∵，∴，∴，∴；当如图1所示，DE在∠AOB内部，OD在∠AOB外部时，由（2）可知此时如图所示，当OD在∠AOB内部，OE在∠AOB外部时，∵OE，OD分别平分∠AOC，∠BOC，∴，，∵，，∴，∴，∴；如图5所示，当OD，OE都在∠AOB内部时，同理可得，，∵，，∴，∴，∴；∴综上所述，或，故答案为：45°或135°．24．解：（1）∵，∴AB=10cm，∵点M、N分别是线段AC、BC的中点，∴CN=BC，CM=AC，∴MN=CM+CN=CN= AC+BC=（AC+BC）=AB=5cm；（2）MN=，理由：∵点M、N分别是线段AC、BC的中点，∴CN=BC，CM=AC，∵AB=acm，∴MN=CM+CN=CN= AC+BC=（AC+BC）=AB=cm；（3）无变化，MN=，理由：如图，∵点M、N分别是线段AC、BC的中点，∴CN=BC，CM=AC，∵，，∴MN=CM-CN= AC-BC=（AC-BC）=；25．（1）∵OD平分，OE平分，∴，，又∵，，∴；故答案是：．（2）方法1：∵OE平分，，∴，∵OD平分，，∴，∴，与之间的关系为：（或）；方法2：∵OD平分，OE平分，∴，，∴，，，，，∵，，∴，与之间的关系为：（或）；（3）∵OD平分，OE平分，∴，，∴．26．解：（1）∵数轴上点A在原点左边，到原点的距离为6个单位长度，点B在原点的右边，从点A走到点B，要经过10个单位长度，∴点A表示-6，点B表示4；（2）设点C表示的数为c，∵点C到点B的距离是点C到原点的距离的3倍，∴|c-4|=3|c|，∴c-4=3c或c-4=-3c，解得c=-2或c=1；（3）设运动时间为t秒，则AM=t，NO=4+2t，∵点P是NO的中点，∴PO=2+t，∴PO-AM=2+t-t=227．解：（1）∵∠AOB＝100°，∠BOC＝60°，∴∠AOC＝∠AOB+∠BOC＝100°+60°＝160°，∵OM平分∠AOC，∴∠MOC＝∠MOA＝∠AOC＝80°，∴∠BOM＝∠AOB﹣∠AOM＝100°﹣80°＝20°，∵ON平分∠BOC，∴∠BON＝∠CON＝30°，∴∠MON＝∠BOM+∠BON＝20°+30°＝50°；（2）∵∠AOB＝α，∠BOC＝β，∴∠AOC＝∠AOB+∠BOC＝α+β，∵OM平分∠AOC，∴∠MOC＝∠MOA＝∠AOC＝（α+β），∴∠BOM＝∠AOB﹣∠AOM＝α﹣（α+β）＝α﹣β，∵ON平分∠BOC，∴∠BON＝∠CON＝β，∴∠MON＝∠BOM+∠BON＝，故∠MON＝；（3）∵AB＝a，BC＝m，∴AC＝AB+BC＝a+m，∵M是AC中点，∴MC＝，∵N是BC中点，∴NC＝，∴MN＝MC﹣NC＝．28．解：（1）经测量得到∠1=120°，∠2=120°，∠3=120°∠1+∠2+∠3=360°，发现：三角形的外角和为360°；如图①：∠1=150°，∠2=150°，∠3=60°∠1+∠2+∠3=360°（2）经测量得到如图②：∠1=70°，∠2=120°，∠3=60°，∠4=110°∴∠1+∠2+∠3+∠4=360°；经测量得到如图②：∠1=150°，∠2=75°，∠3=90°，∠4=45°∴∠1+∠2+∠3+∠4=360°；发现：四边形的外角和为360°；猜想：根据（1）（2）中这些角都是外角，可以猜想多边形的外角和为360°．【点睛】本题考查角的计算，根据所得出的结果对外角和进行猜想是解题关键．