2023龙岩一中高二上学期第二次月考数学试题含答案

这是一份2023龙岩一中高二上学期第二次月考数学试题含答案，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
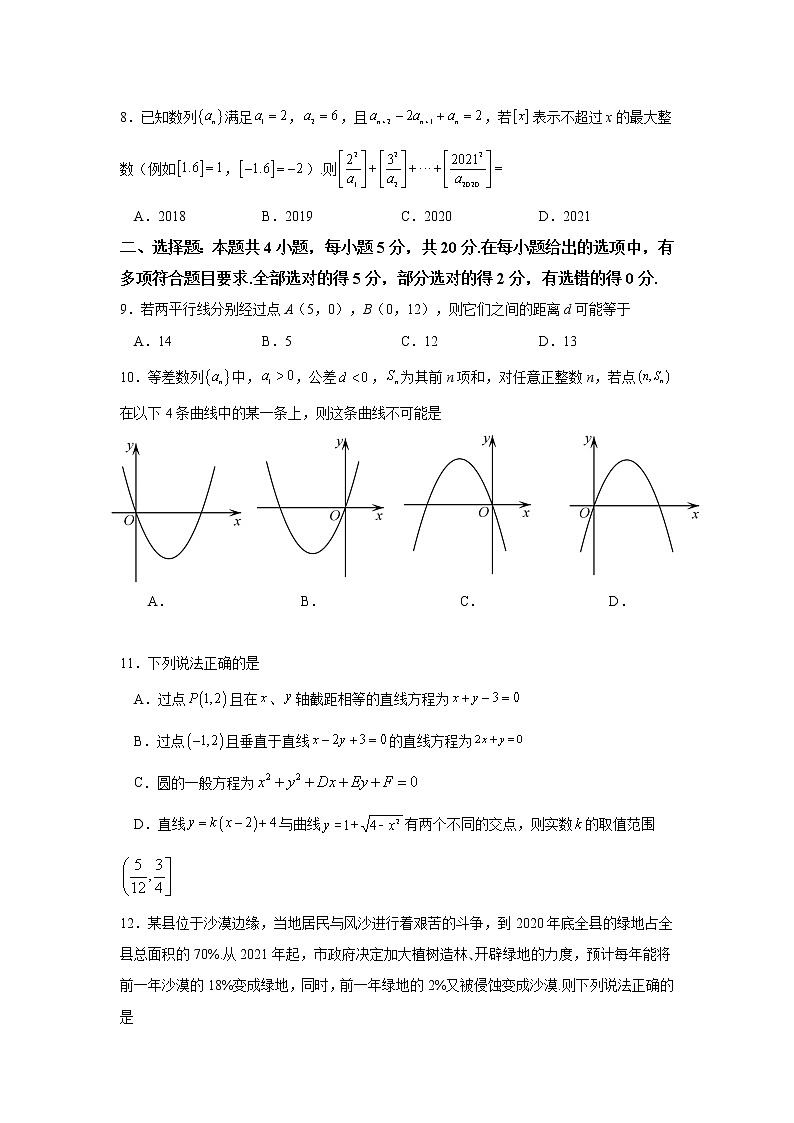
龙岩一中2022-2023学年第一学期高二第二次月考数学试题（考试时间：120分钟   满分：150分） 一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．直线的倾斜角为A．  B．  C．  D．2．已知是等差数列的前项和，若，则A．24  B．36  C．48  D．723．直线与直线互相垂直，则它们的交点坐标为A．  B．  C．  D．4．数列1，，， ，的前n项和为A．  B．  C．  D．5．直线分别与x轴，y轴交于两点，点在圆，则面积的取值范围是A．       B．       C．            D．6．数列A．既有最大项，又有最小项  B．有最大项，无最小项C．无最大项，有最小项  D．既无最大项，又无最小项7．几何学史上有一个著名的米勒问题：“设点M，N是锐角的一边QA上的两点，试在QB边上找一点P，使得最大．”如图，其结论是：点P为过M，N两点且和射线QB相切的圆与射线QB的切点．根据以上结论解决以下问题：在平面直角坐标系xOy中，给定两点M（-1，2），N（1，4），点P在x轴上移动，当取最大值时，点P的横坐标是A．1  B．-7  C．1或-1  D．2或-78．已知数列满足，，且，若表示不超过x的最大整数（例如，）.则A．2018  B．2019  C．2020  D．2021二、选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分. 9．若两平行线分别经过点A（5，0），B（0，12），则它们之间的距离d可能等于A．14  B．5  C．12  D．1310．等差数列中，，公差，为其前n项和，对任意正整数n，若点在以下4条曲线中的某一条上，则这条曲线不可能是     A．       B．          C．                  D． 11．下列说法正确的是A．过点且在、轴截距相等的直线方程为B．过点且垂直于直线的直线方程为C．圆的一般方程为D．直线与曲线有两个不同的交点，则实数的取值范围12．某县位于沙漠边缘，当地居民与风沙进行着艰苦的斗争，到2020年底全县的绿地占全县总面积的70%.从2021年起，市政府决定加大植树造林､开辟绿地的力度，预计每年能将前一年沙漠的18%变成绿地，同时，前一年绿地的2%又被侵蚀变成沙漠.则下列说法正确的是A．2021年底，该县的绿地面积占全县总面积的74%B．2023年底，该县的绿地面积将超过全县总面积的80%C．在这种政策之下，将来的任意一年，全县绿地面积都不能超过90%D．在这种政策之下，将来的某一年，绿地面积将达到100%全覆盖三、填空题：本题共4小题，每小题5分，共20分. 13．数列中，则_____________．14．设是公差为的等差数列，是公比为的等比数列．已知数列的前项和，则的值是_______．15．在直角坐标系中，已知直线，当变化时，动直线始终没有经过点，定点的坐标，则的取值范围为          ．16．已知动点在圆上，则的取值范围是____________，若点，点，则的最小值为____________．四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17．（10分）已知等比数列    的首项，公比，数列．(1)证明：数列    为等差数列；(2)设数列前项和为，求使        的所有正整数  的值的和．18. （12分）已知圆的方程为：.（1）试求的值，使圆的周长最小；（2）求与满足（1）中条件的圆相切，且过点的直线方程．19．（12分）记为数列的前项和，已知是公差为的等差数列．(1)求的通项公式；(2)记                    ，试判断与2的大小并证明．20. （12分）已知圆，直线.(1)求证：对 ，直线与圆总有两个不同的交点；(2)若直线与圆交于两点，当时，求直线的倾斜角．21．（12分）已知数列满足，．（1）求证：数列是等比数列，并求数列的通项公式；（2）记数列的前项中最大值为，最小值为，令，称数列是数列的“中程数数列”．（i）求“中程数数列”的前项和；（ii）若（且），求所有满足条件的实数对．22．（12分）平面直角坐标系中，圆M经过点，，．(1)求圆M的标准方程；(2)设，过点D作直线，交圆M于PQ两点，PQ不在y轴上．（i）过点D作与直线垂直的直线，交圆M于EF两点，记四边形EPFQ的面积为S，求S的最大值；（ii）设直线OP，BQ相交于点N，试讨论点N是否在定直线上，若是，求出该直线方程；若不是，说明理由．      龙岩一中2022-2023学年第一学期高二第二次月考数学试题参考答案 题号123456789101112答案CBBBCAADBCDABCBDAC 13．   14．4   15．   16．     17.(1)证明：因为等比数列的首项，公比，所以，...................2分所以，............................3分所以，，所以是首项为，公差为的等差数列；.................5分(2)解：由（1）可得，所以，....................6分令，解得，........................8分又，所以、、、、5、6、7、8，.........................9分∴1+2+3+4+5+6+7+8=36∴所有正整数的值的和为36..............................10分18.（1），配方得：，................2分当时，圆的半径有最小值2，此时圆的周长最小...................4分（2）由（1）得，，圆的方程为：.当直线与轴垂直时，，此时直线与圆相切，符合条件；..............6分当直线与轴不垂直时，设，............7分由直线与圆相切得：，解得，..............10分所以切线方程为，即..................................11分综上，直线方程为或......................12分19.(1)∵，∴,∴,又∵是公差为的等差数列，∴,∴,...............3分∴当时，，........................4分∴,......................5分整理得：,即,..........................6分∴，显然对于也成立，∴的通项公式；...........................8分(2) ....................10分∴ ∴...................12分20.（1）证明：直线 的方程可化为，令，解得．∴直线恒过定点．..............3分∵，∴点在圆内，∴直线与圆总有两个不同的交点. ...............6分（2）由消去整理得，显然． ....................8分设，是一元二次方程的两个实根， ∴，....................9分∵，....................10分∴，解得∴，即直线的斜率为....................12分 ∴直线的倾斜角为或....................12分21.解：（1）证明：依题意，，即，故，故数列是等比数列，首项为，公比为的等比数列，故，即；....................4分（2）因为，即，故时，即，时，，即，故，故，，所以.......................6分①设数列的前n项和为，则，，两式作差得，，即，故；....................8分②因为，，，所以，即，又因为，，，且，可知且，即，由知，时，，故，即，但，故符合题意；时，，故，即，但，故无解；时，，故，即，又，故符合题意；综上，所有满足条件的实数对有．...................12分22.(1)解：设圆M的方程为，则，解得，所以圆M的标准方程为；....................4分(2)解：设直线的方程为，即，则圆心到直线的距离，所以，（i）若，则直线斜率不存在，则，，则，若，则直线得方程为，即，则圆心到直线的距离，所以，则，当且仅当，即时，取等号，综上所述，因为，所以S的最大值为7；.................8分（ii）设，联立，消得，则，直线的方程为，直线的方程为，联立，解得，则，所以，所以点N在定直线上...................12分