(新高考)高考数学一轮复习课时练习9.1《直线的倾斜角与斜率、直线方程》(含解析)

这是一份(新高考)高考数学一轮复习课时练习9.1《直线的倾斜角与斜率、直线方程》(含解析)，共15页。试卷主要包含了直线的倾斜角，直线的斜率等内容，欢迎下载使用。

第1讲　直线的倾斜角与斜率、直线方程
最新考纲
考向预测
1.在平面直角坐标系中，结合具体图形，探索确定直线位置的几何要素.
2.理解直线的倾斜角和斜率的概念，经历用代数方法刻画直线斜率的过程，掌握过两点的直线斜率的计算公式.
3.根据确定直线位置的几何要素，探索并掌握直线方程的几何形式(点斜式、两点式及一般式)．
命题趋势
直线是解析几何中最基本的内容，对直线的考查一是在选择题、填空题中考查直线的倾斜角、斜率、直线的方程等基本知识；二是在解答题中与圆、椭圆、双曲线、抛物线等知识进行综合考查.
核心素养
直观想象


1．直线的倾斜角
(1)定义：

(2)范围：直线的倾斜角α的取值范围是[0，π)．
2．直线的斜率
条件
公式
直线的倾斜角θ，且θ≠90°
k＝tan_θ
直线过点A(x1，y1)，B(x2，y2)且x1≠x2
k＝
直线Ax＋By＋C＝0(B≠0)
k＝－
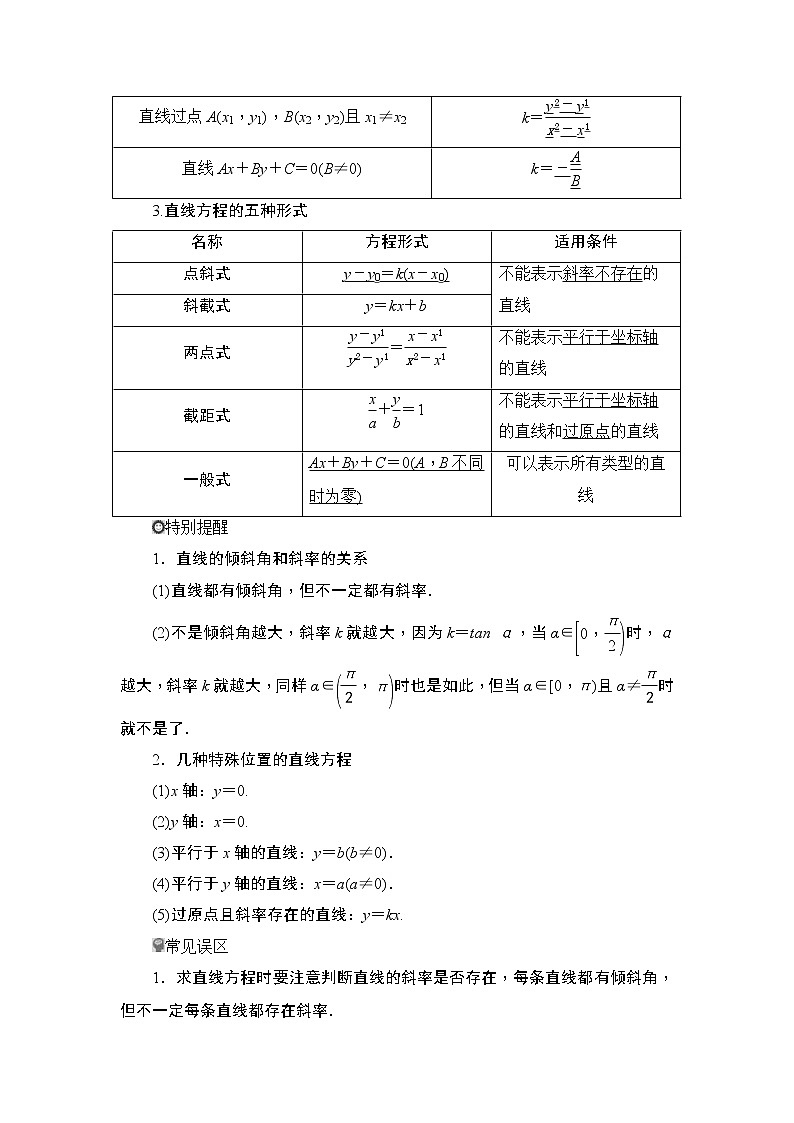
3.直线方程的五种形式
名称
方程形式
适用条件
点斜式
y－y0＝k(x－x0)
不能表示斜率不存在的直线
斜截式
y＝kx＋b
两点式
＝
不能表示平行于坐标轴的直线
截距式
＋＝1
不能表示平行于坐标轴的直线和过原点的直线
一般式
Ax＋By＋C＝0(A，B不同时为零)
可以表示所有类型的直线
特别提醒
1．直线的倾斜角和斜率的关系
(1)直线都有倾斜角，但不一定都有斜率．
(2)不是倾斜角越大，斜率k就越大，因为k＝tan α，当α∈时，α越大，斜率k就越大，同样α∈时也是如此，但当α∈[0，π)且α≠时就不是了．
2．几种特殊位置的直线方程
(1)x轴：y＝0.
(2)y轴：x＝0.
(3)平行于x轴的直线：y＝b(b≠0)．
(4)平行于y轴的直线：x＝a(a≠0)．
(5)过原点且斜率存在的直线：y＝kx.
常见误区
1．求直线方程时要注意判断直线的斜率是否存在，每条直线都有倾斜角，但不一定每条直线都存在斜率．
2．斜率公式k＝(x1≠x2)与两点的顺序无关，且两点的横坐标不相等．
3．“截距”是直线与坐标轴交点的坐标值，它可正，可负，也可以是零，而“距离”是一个非负数．

1．判断正误(正确的打“√”，错误的打“×”)
(1)直线的倾斜角越大，其斜率就越大．(　　)
(2)直线的斜率为tan α，则其倾斜角为α.(　　)
(3)斜率相等的两直线的倾斜角不一定相等．(　　)
(4)经过点P(x0，y0)的直线都可以用方程y－y0＝k(x－x0)表示．(　　)
答案：(1)×　(2)×　(3)×　(4)×
2．直线l：xsin 30°＋ycos 150°＋a＝0的斜率为(　　)
A. B. C．－ D．－
解析：选A.cos 150°＝－，sin 30°＝，所以k＝－＝.
3．(多选)下列说法正确的是(　　)
A．截距相等的直线都可以用方程＋＝1表示
B．方程x＋my－2＝0(m∈R)能表示平行于y轴的直线
C．经过点P(1，1)，倾斜角为θ的直线方程为y－1＝tan θ(x－1)　
D．经过两点P1(x1，y1)，P2(x2，y2)的直线方程为(y2－y1)(x－x1)－(x2－x1)(y－y1)＝0
解析：选BD.对于A，若直线过原点，横纵截距都为0，则不能用方程＋＝1表示，所以A不正确；对于B，当m＝0时，平行于y轴的直线方程为x＝2，所以B正确；对于C，若直线的倾斜角为90°，则该直线的斜率不存在，不能用y－1＝tan θ(x－1)表示，所以C不正确；对于D，设点P(x，y)是经过两点P1(x1，y1)，P2(x2，y2)的直线上的任意一点，则根据∥可得(y2－y1)(x－x1)－(x2－x1)(y－y1)＝0，所以D正确，故选BD.
4．若过点M(－2，m)，N(m，4)的直线的斜率等于1，则m＝________，
解析：由k＝＝1，得4－m＝m＋2，即m＝1.
答案：1
5．过点(－1，2)且倾斜角为150°的直线方程为________．
解析：因为k＝tan 150°＝－，所以直线方程为y－2＝－(x＋1)，即x＋3y－6＋＝0.
答案：x＋3y－6＋＝0


直线的倾斜角与斜率
(1)直线xsin α＋y＋2＝0的倾斜角的取值范围是(　　)
A. B.∪
C. D.∪
(2)直线l过点P(1，0)，且与以A(2，1)，B(0，)为端点的线段有公共点，则直线l斜率的取值范围为________．
【解析】　(1)设直线的倾斜角为θ，则有tan θ＝－sin α.因为sin α∈[－1，1]，所以－1≤tan θ≤1，又θ∈[0，π)，所以0≤θ≤或≤θ＜π，故选B.
(2)如图，因为kAP＝＝1，
kBP＝＝－，所以直线l的斜率k∈∪.
【答案】　(1)B
(2)∪
【引申探究】
1．(变条件)将本例(1)变为：直线2xcos α－y－3＝0的倾斜角的取值范围为________．
解析：直线2xcos α－y－3＝0的斜率k＝2cos α.由于α∈，所以≤cos α≤，因此k＝2cos α∈[1，]．设直线的倾斜角为θ，则有tan θ∈[1，]．由于θ∈[0，π)，所以θ∈，即倾斜角的取值范围是.
答案：
2．(变条件)若将本例(2)中P(1，0)改为P(－1，0)，其他条件不变，求直线l斜率的取值范围．
解：因为P(－1，0)，A(2，1)，B(0，)，所以kAP＝＝，kBP＝＝.
由图可知，直线l斜率的取值范围为.

(1)求倾斜角的取值范围的一般步骤
①求出斜率k＝tan α的取值范围；
②利用三角函数的单调性，借助图象，确定倾斜角α的取值范围．
求倾斜角时要注意斜率是否存在．
(2)斜率的求法
①定义法：若已知直线的倾斜角α或α的某种三角函数值，一般根据k＝tan α求斜率；
②公式法：若已知直线上两点A(x1，y1)，B(x2，y2)，一般根据斜率公式k＝(x1≠x2)求斜率．　

1．(2021·普通高等学校招生全国统一考试模拟)若正方形一条对角线所在直线的斜率为2，则该正方形的两条邻边所在直线的斜率分别为________，________．
答案：　－3
2．若直线l的斜率为k，倾斜角为α，且α∈∪，则k的取值范围是________．
解析：当α∈时，k＝tan α∈；
当α∈时，k＝tan α∈[－，0)．
综上得k∈[－，0)∪.
答案：[－，0)∪

直线的方程
(1)(多选)若直线l过点A(1，2)，且在两坐标轴上截距的绝对值相等，则直线l的方程可能为(　　)
A．x－y＋1＝0 B．x＋y－3＝0
C．2x－y＝0 D．x－y－1＝0
(2)若直线过点A(1，3)，且斜率是直线y＝－4x的斜率的，则该直线的方程为________．
【解析】　(1)当直线经过原点时，斜率为k＝＝2，所求的直线方程为y＝2x，即2x－y＝0；当直线不过原点时，设所求的直线方程为x±y＝k，把点A(1，2)代入可得1－2＝k或1＋2＝k，求得k＝－1或k＝3，故所求的直线方程为x－y＋1＝0或x＋y－3＝0.综上，所求的直线方程为2x－y＝0，x－y＋1＝0或x＋y－3＝0.
故选ABC.
(2)设所求直线的斜率为k，依题意k＝－4×＝－.又直线经过点A(1，3)，因此所求直线的方程为y－3＝－(x－1)，即4x＋3y－13＝0.
【答案】　(1)ABC　(2)4x＋3y－13＝0

求解直线方程的2种方法
直接法
根据已知条件，选择适当的直线方程形式，直接写出直线方程
待定系数法
①设所求直线方程的某种形式；
②由条件建立所求参数的方程(组)；
③解这个方程(组)求出参数；
④把参数的值代入所设直线方程

1．已知△ABC的三个顶点坐标为A(1，2)，B(3，6)，C(5，2)，M为AB的中点，N为AC的中点，则中位线MN所在直线的方程为(　　)
A．2x＋y－12＝0 B．2x－y－12＝0
C．2x＋y－8＝0 D．2x－y＋8＝0
解析：选C.由题知M(2，4)，N(3，2)，中位线MN所在直线的方程为＝，整理得2x＋y－8＝0.
2．经过点(2，1)，且倾斜角比直线y＝－x－1的倾斜角小的直线方程是(　　)
A．x＝2 B．y＝1 C．x＝1 D．y＝2
解析：选A.因为直线y＝－x－1的斜率为－1，则倾斜角为.由已知，所求直线的倾斜角为－＝，斜率不存在，所以过点(2，1)的直线方程为x＝2.

直线方程的综合应用
(一题多解)已知直线l过点M(2，1)，且分别与x轴的正半轴、y轴的正半轴交于A，B两点，O为原点，当△AOB面积最小时，求直线l的方程．
【解】　方法一：设直线l的方程为y－1＝k(x－2)(k0，b>0，因为直线l过点M(2，1)，所以＋＝1，则1＝＋≥2，故ab≥8，故S△AOB的最小值为×ab＝×8＝4，当且仅当＝＝时取等号，此时a＝4，b＝2，故直线l为＋＝1，即x＋2y－4＝0.
【引申探究】　(变问法)本例条件不变，当|MA|·|MB|取得最小值时，求直线l的方程．
解：方法一：由本例3的解析知A，B(0，1－2k)(k0，b>0，＋＝1.
所以|MA|·|MB|＝||·||
＝－·＝－(a－2，－1)·(－2，b－1)
＝2(a－2)＋b－1＝2a＋b－5
＝(2a＋b)－5＝2≥4，当且仅当a＝b＝3时取等号，此时直线l的方程为x＋y－3＝0.

与直线方程有关问题的常见类型及解题策略
(1)求解与直线方程有关的最值问题．先设出直线方程，建立目标函数，再利用基本不等式求解最值．
(2)求直线方程．弄清确定直线的两个条件，由直线方程的几种特殊形式直接写出方程．
(3)求参数值或范围．注意点在直线上，则点的坐标适合直线的方程，再结合函数的单调性或基本不等式求解．　

1．当k>0时，两直线kx－y＝0，2x＋ky－2＝0与x轴围成的三角形面积的最大值为________．
解析：直线2x＋ky－2＝0与x轴交于点(1，0)．由解得y＝，所以两直线kx－y＝0，2x＋ky－2＝0与x轴围成的三角形的面积为×1×＝，又k＋≥2＝2，当且仅当k＝时取等号，故三角形面积的最大值为.
答案：
2．已知直线x＋2y＝2分别与x轴、y轴相交于A，B两点，若动点P(a，b)在线段AB上，则ab的最大值为________．
解析：由题得A(2，0)，B(0，1)，由动点P(a，b)在线段AB上，可知0≤b≤1，且a＋2b＝2，从而a＝2－2b，故ab＝(2－2b)b＝－2b2＋2b＝－2＋.由于0≤b≤1，故当b＝时，ab取得最大值.
答案：

[A级　基础练]
1．倾斜角为120°，在x轴上的截距为－1的直线方程是(　　)
A.x－y＋1＝0 B.x－y－＝0
C.x＋y－＝0 D.x＋y＋＝0
解析：选D.由于倾斜角为120°，故斜率k＝－.又直线过点(－1，0)，所以方程为y＝－(x＋1)，即x＋y＋＝0.
2．(多选)下列说法正确的是(　　)
A．直线x－y－2＝0与两坐标轴围成的三角形的面积是2
B．点(0，2)关于直线y＝x＋1的对称点为(1，1)
C．过两点(x1，y1)，(x2，y2)的直线方程为＝
D．经过点(1，1)且在x轴和y轴上的截距都相等的直线方程为x＋y－2＝0
解析：选AB.A中，直线x－y－2＝0在x轴、y轴上的截距分别为2，－2，则直线与两坐标轴围成的三角形的面积是2，所以A正确．B中，点在直线y＝x＋1上，且点(0，2)，(1，1)连线的斜率为－1，所以B正确．C中，直线方程成立需要条件y2≠y1，x2≠x1，所以C错误．D中，还有一条截距都为0的直线y＝x，所以D错误．故选AB.
3．在等腰三角形MON中，MO＝MN，点O(0，0)，M(－1，3)，点N在x轴的负半轴上，则直线MN的方程为(　　)
A．3x－y－6＝0 B．3x＋y＋6＝0
C．3x－y＋6＝0 D．3x＋y－6＝0
解析：选C.因为MO＝MN，所以直线MN的斜率与直线MO的斜率互为相反数，所以kMN＝－kMO＝3，所以直线MN的方程为y－3＝3(x＋1)，即3x－y＋6＝0，选C.
4．(多选)过点A(1，2)的直线在两坐标轴上的截距之和为零，则该直线方程可能为(　　)
A．x－y＋1＝0 B．x＋y－3＝0
C．2x－y＝0 D．x－y－1＝0
解析：选AC.当直线过原点时，可得斜率为＝2，故直线方程为y＝2x，即2x－y＝0.当直线不过原点时，设直线方程为＋＝1，代入点(1，2)，可得－＝1，解得a＝－1，所以直线方程为x－y＋1＝0，故所求直线方程为2x－y＝0或x－y＋1＝0.故选AC.
5．(2020·四川雅安中学月考)已知直线l1：y＝k1x＋b1与l2：y＝k2x＋b2如图所示，则有(　　)

A. B.
C. D.
解析：选A.由图可知直线l1的倾斜角小于直线l2的倾斜角，并且它们都大于，由y＝tan x在x∈上单调递增，得k1