2020-2021学年3.3 幂函数导学案

这是一份2020-2021学年3.3 幂函数导学案，共1页。
1．理解幂函数的概念．
2．掌握y＝xα(α＝－1，eq \f(1,2)，1,2,3)的图象与性质．
3．理解和掌握幂函数在第一象限的分类特征，能运用数形结合的方法处理幂函数的有关问题．
1．幂函数的概念
一般地，函数y＝xα叫做幂函数，其中x是自变量，α是常数．
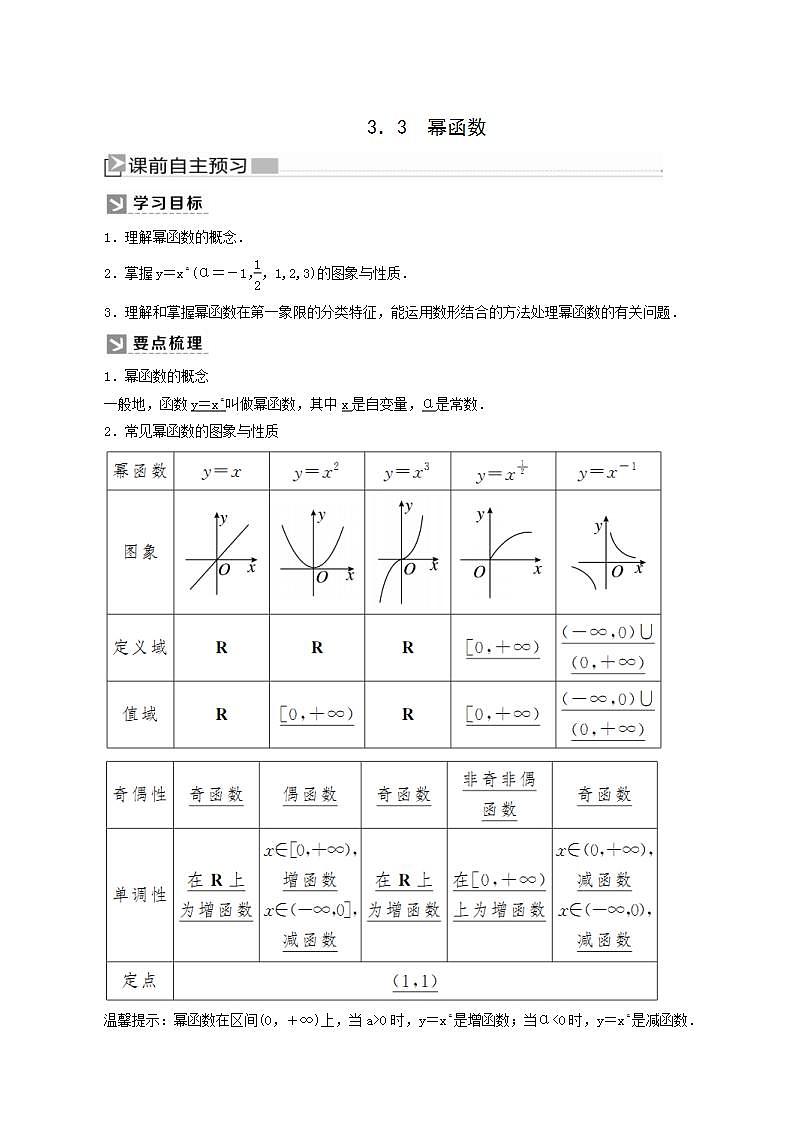
2．常见幂函数的图象与性质
温馨提示：幂函数在区间(0，＋∞)上，当a>0时，y＝xα是增函数；当α0时，y＝xα是增函数．( )
[答案] (1)√ (2)× (3)× (4)×
题型一 幂函数的概念
【典例1】 (1)在函数①y＝eq \f(1,x)，②y＝x2，③y＝2x，④y＝1，⑤y＝2x2，⑥y＝x eq \s\up15(－eq \f (1,2)) 中，是幂函数的是( )
A．①②④⑤B．③④⑥
C．①②⑥D．①②④⑤⑥
(2)已知幂函数y＝(m2－m－1)xm2－2m－3，求此幂函数的解析式，并指出其定义域．
[思路导引] 紧扣幂函数的定义求解．
[解析] (1)幂函数是形如y＝xα(α为常数)的函数，①是α＝－1的情形，②是α＝2的情形，⑥是α＝－eq \f(1,2)的情形，所以①②⑥都是幂函数；③是指数函数，不是幂函数；⑤中x2的系数是2，所以不是幂函数；④是常函数，不是幂函数．所以只有①②⑥是幂函数．故选C.
(2)∵y＝(m2－m－1)x m2－2m－3为幂函数，
∴m2－m－1＝1，解得m＝2或m＝－1.
当m＝2时，m2－2m－3＝－3，则y＝x－3，且有x≠0；
当m＝－1时，m2－2m－3＝0，则y＝x0，且有x≠0.
故所求幂函数的解析式为y＝x－3或y＝x0，它们的定义域都是{x|x≠0}．
[答案] (1)C (2)见解析
判断一个函数是否为幂函数的方法
判断一个函数是否为幂函数的依据是该函数是否为y＝xα(α为常数)的形式，即函数的解析式为一个幂的形式，且需满足：(1)指数为常数；(2)底数为自变量；(3)系数为1.
[针对训练]
1．下列函数中不是幂函数的是( )
A．y＝eq \r(x)B．y＝x eq \s\up15(eq \r(3))
C．y＝22xD．y＝x－1
[解析] 函数y＝22x＝4x不是幂函数，故选C.
[答案] C
2．若幂函数f(x)满足f(9)＝3，则f(100)＝________.
[解析] 设f(x)＝xα，由f(9)＝3，得9α＝3，
∴α＝eq \f(1,2)，∴f(x)＝x eq \s\up15( eq \f (1,2)) ，
∴f(100)＝100 eq \s\up15( eq \f (1,2)) ＝10.
[答案] 10
题型二 幂函数的图象与性质
【典例2】 已知幂函数f(x)＝xα的图象过点Peq \b\lc\(\rc\)(\a\vs4\al\c1(2，\f(1,4)))，试画出f(x)的图象并指出该函数的定义域与单调区间．
[思路导引] 求出α，结合图象确定定义域和值域．
[解] 由f(2)＝eq \f(1,4)，得2α＝eq \f(1,4)，
解得α＝－2，所以f(x)＝x－2.
f(x)的图象如图所示，定义域为(－∞，0)∪(0，＋∞)，单调减区间为(0，＋∞)，单调增区间为(－∞，0)．
[变式] (1)本例条件不变，试判断f(x)的奇偶性．
(2)本例中点P变为eq \b\lc\(\rc\)(\a\vs4\al\c1(8，\f(1,2)))，判断函数f(x)的奇偶性与单调性．
[解] (1)由f(－x)＝(－x)－2＝x－2＝f(x)，
得f(x)是偶函数．
(2)由f(8)＝eq \f(1,2)，得8α＝eq \f(1,2)，解得α＝－eq \f(1,3)，所以f(x)＝x eq \s\up15(－eq \f(1,3)) ，其定义域为(－∞，0)∪(0，＋∞)，是奇函数，在(－∞，0)和(0，＋∞)上都是减函数．
解决幂函数图象问题应把握的2个原则
(1)依据图象高低判断幂指数大小，相关结论为：在(0,1)上，指数越大，幂函数图象越靠近x轴(简记为指大图低)；在(1，＋∞)上，指数越大，幂函数图象越远离x轴(简记为指大图高)．
(2)依据图象确定幂指数α与0,1的大小关系，即根据幂函数在第一象限内的图象(类似于y＝x－1或y＝x eq \s\up15( eq \f (1,2)) 或y＝x3)来判断．
[针对训练]
3．如图，图中曲线是幂函数y＝xα在第一象限的大致图象，已知α取－2，－eq \f(1,2)，eq \f(1,2)，2四个值，则相应于曲线C1，C2，C3，C4的α的值依次为( )
A．－2，－eq \f(1,2)，eq \f(1,2)，2
B．2，eq \f(1,2)，－eq \f(1,2)，－2
C．－eq \f(1,2)，－2,2，eq \f(1,2)
D．2，eq \f(1,2)，－2，－eq \f(1,2)
[解析] 令x＝2，则22>2 eq \s\up15( eq \f (1,2)) >2 eq \s\up15(－eq \f (1,2)) >2－2，故相应于曲线C1，C2，C3，C4的α值依次为2，eq \f(1,2)，－eq \f(1,2)，－2.故选B.
[答案] B
4．如图是幂函数y＝xm与y＝xn在第一象限内的图象，则( )
A．－1