初中数学人教版七年级上册第二章 整式的加减综合与测试学案

这是一份初中数学人教版七年级上册第二章 整式的加减综合与测试学案，共16页。

第5讲 一元一次方程
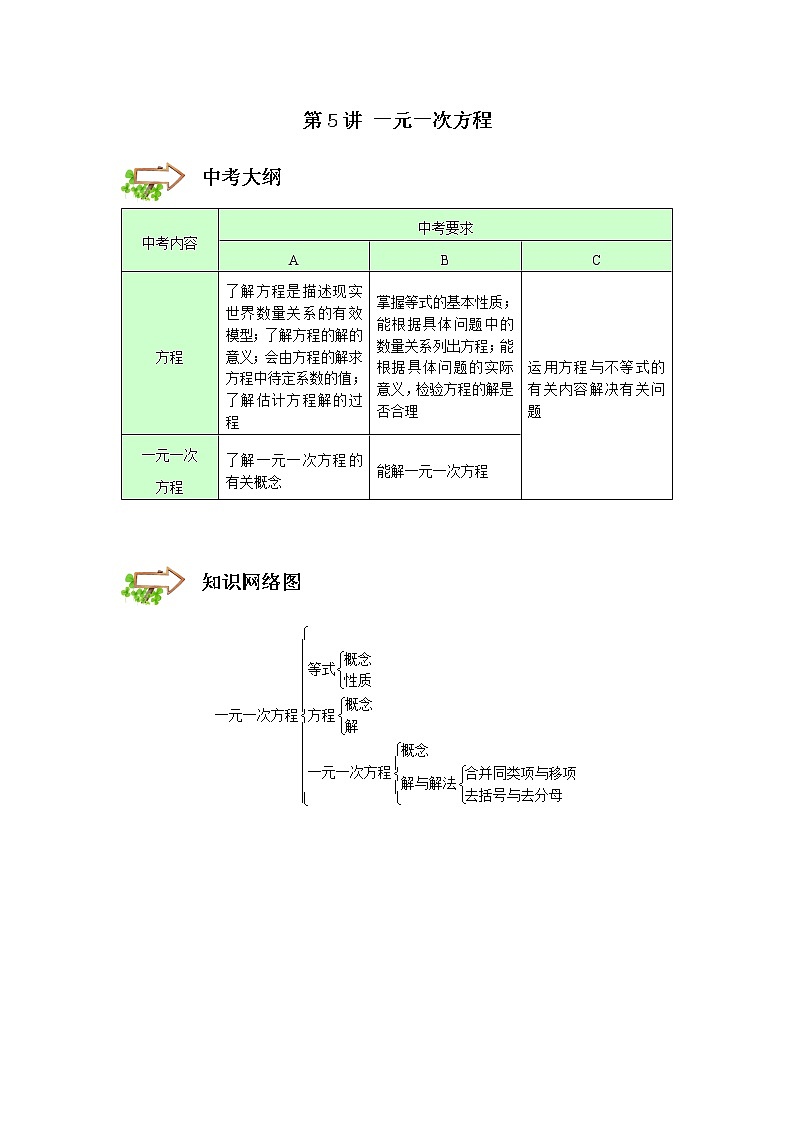
中考大纲

中考内容
中考要求
A
B
C
方程
了解方程是描述现实世界数量关系的有效模型；了解方程的解的意义；会由方程的解求方程中待定系数的值；了解估计方程解的过程
掌握等式的基本性质；能根据具体问题中的数量关系列出方程；能根据具体问题的实际意义，检验方程的解是否合理
运用方程与不等式的有关内容解决有关问题
一元一次
方程
了解一元一次方程的有关概念
能解一元一次方程

知识网络图




1等式与方程
知识概述


一． 等式
1. 等式的概念：含有等号的式子叫做等式．
在等式中，等号左、右两边的式子，分别叫做这个等式的左边、右边．
等式可以是数字算式，可以是公式、方程，也可以是用式子表示的运算律、运算法则．
2. 等式的性质：
（1） 等式的性质1：等式两边加（或减）同一个数（或式子），结果仍相等．
如果，那么
（2） 等式的性质2：等式两边乘同一个数，或除以同一个不为的数，结果仍相等．
如果，那么；
如果，那么.
注意：①在对等式变形过程中，等式两边必须同时进行．
②同时加或同时减，同时乘以或同时除以，不能漏掉某一边．
③等式变形过程中，两边同加或同减，同乘或同除以的数或整式必须相同．
④在等式变形中，以下两个性质也经常用到：
3. 等式的对称性，即：如果，那么．
4. 等式的传递性，即：如果，，那么（又称为等量代换）．
5. 移项：把等式一边的某项变号后移到另一边，叫做移项．
二． 方程
方程的概念：含有未知数的等式叫做方程．
它有两层含义：① 方程必须是等式；② 等式中必须含有未知数．

小试牛刀


【例】（2018•枣庄）如图，将边长为3a的正方形沿虚线剪成两块正方形和两块长方形．若拿掉边长2b的小正方形后，再将剩下的三块拼成一块矩形，则这块矩形较长的边长为（　　）

A．3a+2b B．3a+4b C．6a+2b D．6a+4b
【解答】解：依题意有
3a﹣2b+2b×2
=3a﹣2b+4b
=3a+2b．
故这块矩形较长的边长为3a+2b．
故选：A．
再接再厉


【例】（2018•繁昌县二模）某工厂二月份的产值比一月份的产值增长了x%，三月份的产值又比二月份的产值增长了x%，则三月份的产值比一月份的产值增长了（　　）
A．2x% B．1+2x% C．（1+x%）x% D．（2+x%）x%
【解答】解：设一月份的产值为a，则二月份的产值为：a（1+x%），
故三月份的产值为：a（1+x%）2，
则三月份的产值比一月份的产值增长了﹣1=（2+x%）x%．
故选：D．
【练习】（2018•禹会区二模）某企业今年3月份产值为m万元，4月份比3月份减少了8%，预测5月份比4月份增加9%，则5月份的产值是（　　）
A．（m﹣8%）（m+9%）万元 B．（1﹣8%）（1+9%）m万元
C．（m﹣8%+9%）万元 D．（m﹣8%+9%）m万元
【解答】解：由题意可得，
5月份的产值是：m（1﹣8%）（1+9%）万元，
故选：B．
【练习】（2017秋•金堂县期末）某地电话拨号入网有两种收费方式，用户可任选其一：A．记时制：3元/时；B．包月制：50元/月（限一部个人住宅电话入网）．此外，每一种上网方式都得加收通讯费1.2元/时．
（1）某用户某月的上网时间为x小时，请写出两种收费方式下该用户应该支付的费用；
（2）若某用户估计一个月的上网时间为25小时，你认为选择哪种方式较合算．
【解答】解：（1）采用记时制应付的费用为3x+1.2x=4.2x（元），
采用包月制应付的费用为（50+1.2x）元；

（2）若一个月内上网的时间为25小时，则计时制应付的费用为4.2×25=105（元），
包月制应付的费用为50+1.2×25=80（元）．
∵105＞80
∴包月制合算．
总述

等式的变形问题
考点：等式的两个基本性质，一定要牢记成立的条件．
易错点：两边同时乘或除以一个字母（式子）时，一定要保证该字母（式子）不为零．
做题方法：牢记“”这个特殊情况，用赋值法检验．




2方程的解
知识概述
知识网络图


一． 方程的解：使方程中等号左右两边相等的未知数的值，叫做方程的解．
1. 只含有一个未知数的方程的解，也叫方程的根．
2. 求解的过程就是解方程．
二． 关于方程中的未知数和已知数：
1. 已知数：一般是具体的数值，如中（的系数是，是已知数．但可以不说．）和是已知数，如果方程中的已知数需要用字母表示的话，习惯上用、、、、等表示．
2. 未知数：是指要求的数，未知数通常用、、等字母表示．如：关于、的方程中，、、是已知数，、是未知数．
小试牛刀


【例】（2017秋•大安市期末）关于x的方程2﹣（1﹣x）=0与方程mx﹣3（5﹣x）=﹣3的解互为相反数，求m的值．
【解答】解：解方程2﹣（1﹣x）=0得x=﹣1，
所以方程mx﹣3（5﹣x）=﹣3的解为x=1，
将x=1代入mx﹣3（5﹣x）=﹣3，得：m﹣3×4=﹣3，
解得：m=9．
再接再厉


【例】（2017秋•平谷区期末）阅读材料：规定一种新的运算：=ad﹣bc．例如：=1×4﹣2×3=﹣2．
（1）按照这个规定，请你计算的值．
（2）按照这个规定，当=5时求x的值．
【解答】解：（1）=20﹣12=8
（2）由 ，
得：
解得，x=1
【练习】（2017秋•凌海市期末）解方程：﹣（3x+4）=﹣．
【解答】解：去分母得，（x﹣4）﹣2（3x+4）=﹣15，
去括号得，x﹣4﹣6x﹣8=﹣15，
移项得，x﹣6x=﹣15+4+8，
合并同类项得，﹣5x=﹣3，
系数化为1得，x=．
总述

解题方法总结：
（1）若已知解，求字母的值时，则直接代入方程。
（2）判断是否是方程的解时，代入方程验证。
（3）同解问题，先解出其中一个方程，代入另一个含有字母的方程即可。







3一元一次方程
知识概述


一． 一元一次方程的概念：只含有一个未知数（元），未知数的次数是，等号两边都是整式，这样的方程叫做一元一次方程．
注意：这里的“元”是指未知数，“次”是指含未知数的项的最高次数．
二． 一元一次方程的形式：
1. 最简形式：方程（，，为已知数）叫一元一次方程的最简形式．
2. 标准形式：方程（其中，，是已知数）叫一元一次方程的标准形式．
注意：
（1） 任何一元一次方程都可以转化为最简形式或标准形式，所以判断一个方程是不是一元一次方程，可以通过变形（必须为恒等变换）为最简形式或标准形式来验证．
如：方程是一元一次方程．如果不变形，直接判断就出会现错误．
（2） 方程与方程是不同的，方程的解需要分类讨论完成．
小试牛刀


【例】（2017秋•南充期末）若（m﹣1）x|m|+5=0是一元一次方程，则m的值为（　　）
A．1 B．﹣1 C．±1 D．不能确定
【解答】解：由题意，得，
解得：m=﹣1．
故选：B．
再接再厉


【练习】（2017秋•凉州区期末）当m为何值时，关于x的方程5m+12x=6+x的解比关于x的方程x（m+1）=m（1+x）的解大2．
【解答】解：解关于x的方程5m+12x=6+x，得：x=，
解关于x的方程x（m+1）=m（1+x），得：x=m，
根据题意得﹣m=2，
解得：m=﹣1．
【例】（2017秋•顺义区期末）我们规定：若关于x的一元一次方程ax=b的解为b+a，则称该方程为“和解方程”． 例如：方程2x=﹣4的解为x=﹣2，而﹣2=﹣4+2，则方程2x=﹣4为“和解方程”．
请根据上述规定解答下列问题：
（1）已知关于x的一元一次方程3x=m是“和解方程”，求m的值；
（2）已知关于x的一元一次方程﹣2x=mn+n是“和解方程”，并且它的解是x=n，求m，n的值．
【解答】解：（1）∵方程3x=m是和解方程，
∴=m+3，
解得：m=﹣．

（2）∵关于x的一元一次方程﹣2x=mn+n是“和解方程”，并且它的解是x=n，
∴﹣2n=mn+n，且mn+n﹣2=n，
解得m=﹣3，n=﹣．
【例】（2017秋•鄂城区期末）已知当x=﹣1时，代数式2mx3﹣3mx+6的值为7．
（1）若关于y的方程2my+n=11﹣ny﹣m的解为y=2，求n的值；
（2）若规定[a]表示不超过a的最大整数，例如[4.3]=4，请在此规定下求[m﹣n]的值．（n为（1）中求出的数值）
【解答】解：（1）把x=﹣1代入得：﹣2m+3m+6=7，
解得：m=1，
把m=1，y=2代入得：4+n=11﹣n×2﹣1，
解得：n=2；
（2）把m=1，n=2代入得：m﹣n=1﹣×2=1﹣3.5=﹣2.5，
则[m﹣n]=[﹣2.5]=﹣3．
　总述

判断是否是一元一次方程，要看是否满足下面的条件：
1． 观察给出的式子，若含有、、，则不是一元一次方程；
2． 若不含上述式子，则进行化简整理，整理后只含有一个未知数，且次数为1，则是一元一次方程；
3． 化简后不能含有、、、、等形式；









4一元一次方程的解法
知识概述


一． 解方程：解方程就是求出使方程中等号左右两边相等的未知数的值，这个值就是方程的解．
二． 解一元一次方程的一般步骤：
变形名称
依据
注意事项
去分母
等式性质2
① 不含分母的项不要漏乘
② 注意分数线有括号作用，去掉分母后，如果分子是多项式，要加括号
去括号
分配律，去括号法则
① 运用分配律去括号时，不要漏乘括号内的项
② 如果括号前是“－”号，去括号时，括号内各项要变号
移项
等式性质1
① 移项必须变号
② 一般把含未知数的项移到左边，其他项移到右边
合并同类项
合并同类项法则
合并同类项是系数相加，字母及其指数不变
系数化为1
等式性质2
分子、分母不要颠倒

小试牛刀


【例】（2017秋•延边州期末）已知关于x的方程（m﹣2）x|m﹣1|﹣3=0是一元一次方程，则m的值是（　　）
A．2 B．0 C．1 D．0 或2
【解答】解：由题意，得
|m﹣1|=1，且m﹣2≠0，
解得m=0，
故选：B．
【练习】（2017秋•桐梓县期末）若关于x的方程mxm﹣2﹣m+3=0是一元一次方程，则这个方程的解是（　　）
A．x=0 B．x=3 C．x=﹣3 D．x=2
【解答】解：由一元一次方程的特点得m﹣2=1，即m=3，
则这个方程是3x=0，
解得：x=0．
故选：A．
再接再厉


【例】解方程：（2）．
（2）去分母得，2（x﹣7）﹣3（1+x）=6，
去括号得，2x﹣14﹣3﹣3x=6，
移项得，2x﹣3x=6+14+3，
合并同类项得，﹣x=23，
系数化为1得，x=﹣23．
【例】（2017秋•苍溪县期末）我们规定，若关于x的一元一次方程ax=b的解为b﹣a，则称该方程为“差解方程”，例如：2x=4的解为2，且2=4﹣2，则该方程2x﹣4是差解方程．
（1）判断3x=4.5是否是差解方程；
（2）若关于x的一元一次方程5x=m+1是差解方程，求m的值．
【解答】解：（1）∵3x=4.5，
∴x=1.5，
∵4.5﹣3=1.5，
∴3x=4.5是差解方程；

（2）∵关于x的一元一次方程5x=m+1是差解方程，
∴m+1﹣5=，
解得：m=．
故m的值为．
总述

解方程时容易犯下面的错误，要特别注意：
变形名称
依据
注意事项
去分母
等式性质2
① 不含分母的项不要漏乘
② 注意分数线有括号作用，去掉分母后，如果分子是多项式，要加括号
去括号
分配律，去括号法则
① 运用分配律去括号时，不要漏乘括号内的项
② 如果括号前是“－”号，去括号时，括号内各项要变号
移项
等式性质1
① 移项必须变号
② 一般把含未知数的项移到左边，其他项移到右边
合并同类项
合并同类项法则
合并同类项是系数相加，字母及其指数不变
系数化为1
等式性质2
分子、分母不要颠倒


综合练习
一．选择题（共2小题）
1．解方程+＝0时，去分母正确的是（　　）
A．4（2x﹣1）+9x﹣4＝12 B．4（2x﹣1）+3（3x﹣4）＝12
C．8x﹣1+9x+12＝0 D．4（2x﹣1）+3（3x﹣4）＝0
【解答】解：+＝0
在方程两边同乘以12，即可得
4（2x﹣1）+3（3x﹣4）＝0
∴去分母正确的是答案D．
故选：D．
2．下列变形中：①将方程3x＝﹣4的系数化为1，得x＝﹣；②将方程5＝2﹣x移项得x＝5﹣2；③将方程2（2x﹣1）﹣3（x﹣3）＝1去括号得4x﹣2﹣3x﹣9＝1；④将方程＝1+去分母得2（2x﹣1）＝1+3（x﹣3），其中正确的变形有（　　）
A．0个 B．1个 C．2个 D．3个
【解答】解：①将方程3x＝﹣4的系数化为1，得x＝﹣，错误；
②将方程5＝2﹣x移项得x＝2﹣5，错误；
③将方程2（2x﹣1）﹣3（x﹣3）＝1去括号得4x﹣2﹣3x+9＝1，错误；
④将方程＝1+去分母得2（2x﹣1）＝6+3（x﹣3），错误；
故选：A．
二．填空题（共2小题）
3．设a，b，c，d为有理数，现规定一种新的运算＝ad﹣bc，则满足等式＝4的x的值为　　．
【解答】解：根据题意得：
5x﹣3（x+1）＝4，
去括号得：5x﹣3x﹣3＝4，
移项得：5x﹣3x＝4+3，
合并同类项得：2x＝7，
系数化为1得：x＝，
故答案为：．
4．当代数式2x﹣2与3+x的值相等时，x＝　5　．
【解答】解：根据题意得：2x﹣2＝3+x，
移项合并得：x＝5，
故答案为：5．
三．解答题（共4小题）
5．解方程：
（1）4x+3＝2（x﹣1）+1；
（2）x；
（3）；
（4）x﹣+2．
【解答】解：
（1）原式去括号得：
4x+3＝2x﹣1
移项并合并同类项得，2x＝﹣4
系数化为1得，x＝﹣2
（2）原式去分母得，4（3x+7）＝28﹣21x
去括号得，12x+28＝28﹣21x
移项合并同类项得，33x＝0
系数化为1得，x＝0
（3）原式去括号得，x﹣4＝2
移项得，x＝6
（4）原式去分母得，18x﹣3（2﹣18x）＝2x+36
去括号得，18x﹣6+54x＝2x+36
移项合并同类项得，70x＝42
系数化为1得，x＝
6．解方程：
（1）x﹣3（x+1）﹣1＝2x
（2）y﹣＝3+
【解答】解：（1）去括号得：x﹣3x﹣3﹣1＝2x，
移项得：x﹣3x﹣2x＝3+1，
合并同类项得：﹣4x＝4，
系数化为1得：x＝﹣1，
（2）原方程可整理得：y﹣（4y+20）＝3+，
方程两边同时乘以2得：2y﹣2（4y+20）＝6+（y+3），
去括号得：2y﹣8y﹣40＝6+y+3，
移项得：2y﹣8y﹣y＝6+3+40，
合并同类项得：﹣7y＝49，
系数化为1得：y＝﹣7．
7．解方程：
（1）x﹣9＝4x+27
（2）1﹣x＝3x+
（3）12（2﹣3x）＝4x+4
（4）＝
（5）﹣＝1
（6）﹣＝12
【解答】解：（1）移项得：x﹣4x＝27+9，
合并同类项得：﹣3x＝36，
系数化为1得：x＝﹣12，
（2）方程两边同时乘以2得：2﹣3x＝6x+5，
移项得：﹣3x﹣6x＝5﹣2，
合并同类项得：﹣9x＝3，
系数化为1得：x＝﹣，
（3）去括号得：24﹣36x＝4x+4，
移项得：﹣36x﹣4x＝4﹣24，
合并同类项得：﹣40x＝﹣20，
系数化为1得：x＝，
（4）方程两边同时乘以24得：4（2x﹣1）＝3（5x+1），
去括号得：8x﹣4＝15x+3，
移项得：8x﹣15x＝3+4，
合并同类项得：﹣7x＝7，
系数化为1得：x＝﹣1，
（5）方程两边同时乘以6得：2（2x+1）﹣（5x﹣1）＝6，
去括号得：4x+2﹣5x+5＝6，
移项得：4x﹣5x＝6﹣5﹣2，
合并同类项得：﹣x＝﹣1，
系数化为x＝1，
（6）原方程可整理得：﹣（2x+4）＝12，
方程两边同时乘以3得：10x﹣10﹣3（2x+4）＝36，
去括号得：10x﹣10﹣6x﹣12＝36，
移项得：10x﹣6x＝36+12+10，
合并同类项得：4x＝58，
系数化为1得：x＝．
8．化简或解方程：
（1）化简：3a2﹣[5a﹣（2a﹣3）+4a2]
（2）解方程：+1＝
【解答】解：（1）3a2﹣[5a﹣（2a﹣3）+4a2]
＝3a2﹣[5a﹣2a+3+4a2]
＝3a2﹣5a+2a﹣3﹣4a2
＝﹣a2﹣3a﹣3；
（2）+1＝，
2（2x﹣1）+6＝2x+1，
4x﹣2+6＝2x+1，
4x﹣2x＝1+2﹣6，
2x＝﹣3，
x＝﹣1.5．