2021学年29.5 正多边形与圆说课课件ppt

这是一份2021学年29.5 正多边形与圆说课课件ppt，共19页。PPT课件主要包含了正多边形，各边相等，各角相等，外接圆的圆心，正多边形的中心，外接圆的半径，正多边形的半径，每一条边所对的圆心角，正多边形的中心角，弦心距等内容，欢迎下载使用。

问题：观看下面这些美丽的图案,都是在日常生活中经常能看到的.你能从这些图案中找出类似的图形吗?
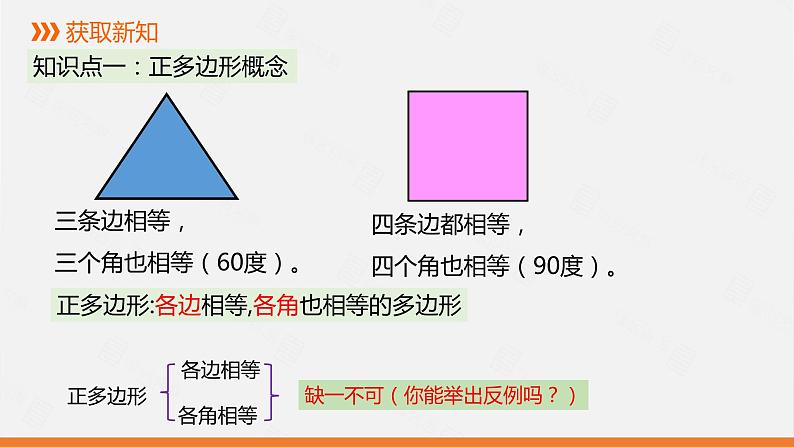
正多边形:各边相等,各角也相等的多边形
三条边相等，三个角也相等（60度）。
四条边都相等，四个角也相等（90度）。
缺一不可（你能举出反例吗？）
知识点一：正多边形概念
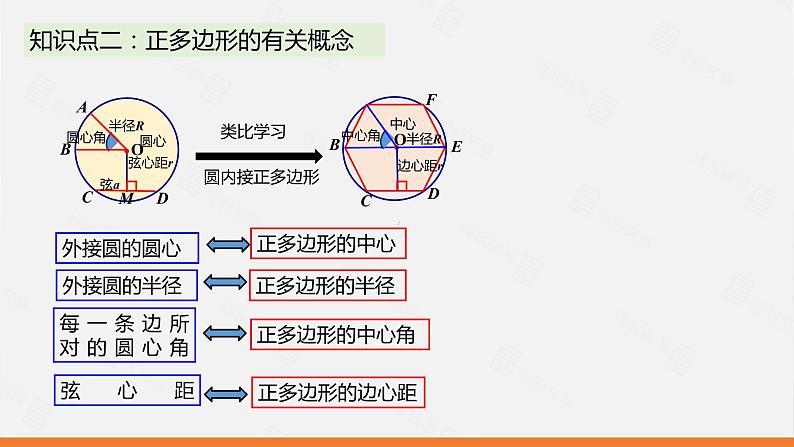
知识点二：正多边形的有关概念
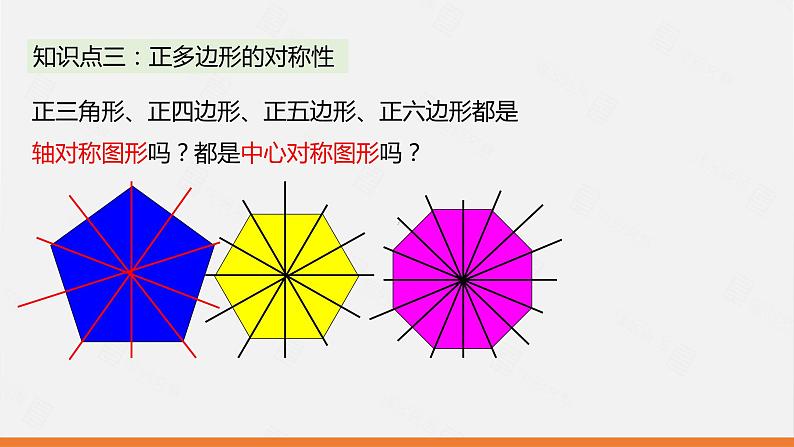
知识点三：正多边形的对称性
正三角形、正四边形、正五边形、正六边形都是轴对称图形吗？都是中心对称图形吗？
n为奇数时，正多边形只是轴对称图形； n为偶数时，既是轴对称图形，又是中心对称图形.对称轴： 为各边的垂直平分线对称中心：正多边形的中心
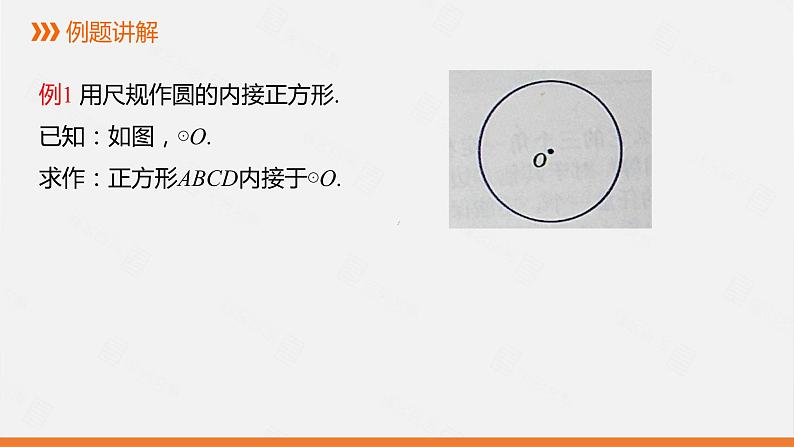
例1 用尺规作圆的内接正方形.已知：如图，⊙O.求作：正方形ABCD内接于⊙O.
作法：(1)如图，作两条互相垂直的直径AC，BD.(2)顺次连接 AB，BC，CD，DA.由作图过程可知，四个中心角都是90°，所以AB=BC= CD=DA.因为AC，BD都是直径，所以∠ABC = ∠BCD= ∠CDA= ∠DAB=90°.即四边形ABCD为⊙O的内接正方形.
例2 如图所示,△ABC为☉O的内接正三角形.如果☉O的半径为r,求这个正三角形的边长和边心距.
解:如图所示,连接OB,过点O作OD⊥BC,垂足为D.
在Rt△OBD中,∵∠OBD=30°,OB=r,
1.下列说法不正确的是(　　)A．等边三角形是正多边形B．各边相等，各角也相等的多边形是正多边形C．菱形不一定是正多边形D．各角相等的多边形是正多边形
2. 下列圆的内接正多边形中，一条边所对的圆心角最大的图形是(　　)A．正三角形 B．正方形C．正五边形 D．正六边形
3. 如图，AD为⊙O的直径，作⊙O的内接正三角形ABC，甲、乙两人的作法分别如下：甲：(1)以D为圆心，OD长为半径画圆弧，交⊙O于B，C两点； (2)连接AB，BC，AC.△ABC即为所求作的三角形．乙：(1)作OD的中垂线，交⊙O于B，C两点； (2)连接AB，AC.△ABC即为所求作的三角形．对于甲、乙两人的作法，可判断(　　)A．甲对，乙不对 B．甲不对，乙对C．两人都对 D．两人都不对
5. 若正多边形的边心距与半径的比为1:2，则这个多边形的边数是 .
6.如图所示,AD是正五边形ABCDE的一条对角线,则∠BAD=　　　　. 
7. 有一个亭子,它的地基是半径为4 m的正六边形,求地基的周长和面积 (精确到0.1 m2).
利用勾股定理,可得边心距
解：过点O作OM⊥BC于M.
8.用尺规作图(不要求写作法和证明,但要保留作图痕迹).(1)如图,已知正五边形ABCDE,求作它的中心O. (2)如图,已知☉O,求作☉O的内接正八边形.
解:(1)如图①,点O即为所求.
(2)如图②,八边形ABCDEFGH即为所求.
正多边形的有关概念及性质
添加辅助线的方法：连半径，作边心距