高中数学人教A版 (2019)必修 第一册5.1 任意角和弧度制示范课课件ppt

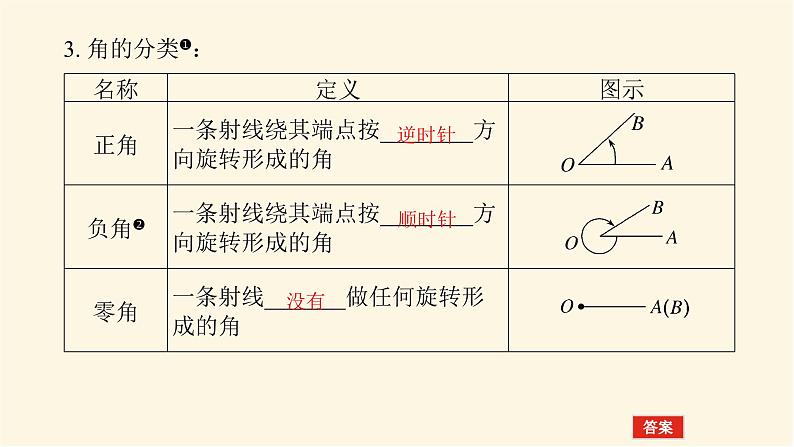
这是一份高中数学人教A版 (2019)必修 第一册5.1 任意角和弧度制示范课课件ppt，共30页。PPT课件主要包含了新知初探·课前预习，角的分类❶，逆时针，顺时针，α＋β，α＋－β，x轴的非负半轴，象限角，坐标轴上，答案D等内容，欢迎下载使用。
课程标准(1)了解任意角的概念，区分正角、负角与零角．(2)理解象限角的概念．(3)理解并掌握终边相同的角的概念，能熟练写出终边相同的角所组成的集合．
教 材 要 点要点一　任意角1．角的概念：角可以看成平面内一条 _______绕着它的端点旋转所成的图形．2．角的表示：如图所示，角α可记为“α”或“∠α”或“∠AOB”，始边：________，终边：__________ ，顶点O.
要点二　角的加法与减法(1)如果角α和角β的旋转方向相同且旋转量相等，那么就称α＝β.(2)设α，β是任意两个角，把角α的终边旋转角β，这时终边所对应的角是______．(3)相反角：把射线OA绕端点O按不同方向旋转相同的量所成的两个角叫做互为相反角，角α的相反角记为－α，于是有α－β＝_________．
要点三　象限角❸把角放在平面直角坐标系中，使角的顶点与原点重合，角的始边与_____________重合，那么角的终边在第几象限，就说这个角是第几________；如果角的终边在________，就认为这个角不属于任何一个象限．要点四　终边相同的角所有与角α终边相同的角，连同角α在内，可构成一个集合S＝____________________❹，即任一与角α终边相同的角，都可以表示成角α与整数个周角的和．
{β|β＝α＋k·360°，k∈Z}
助 学 批 注批注❶　要注意由旋转方向来确定角的符号．批注❷　正角、负角的引入是从正数、负数类比而来的，它们是用来表示具有相反意义的旋转量的．批注❸　象限角只能反映角的终边所在象限，不能反映角的大小．批注❹　(1)角α为任意角，“k∈Z”不能省略．(2)k ·360 °与α中间要用“＋”连接，k ·360 °－α可理解成k ·360 °＋(－α).
基 础 自 测1．思考辨析(正确的画“√”，错误的画“×”)(1)第一象限角都是锐角．(　　)(2)第二象限角是钝角．(　　)(3)终边与始边重合的角为零角．(　　)(4)终边相同的角有无数个，它们相差360°的整数倍.(　　)
2．手表时针走1小时转过的角度是(　　)A．60°　　　B．－60° C．30°　　　D．－30°
3．与53°角终边相同的角是(　　)A．127° B．233°C．－307° D．－127°
解析：与53°角终边相同的角是53°＋k·360°，k∈Z，当k＝－1时，角为－307°.故选C.
4．2 022°是第________象限角．
解析：∵2 022°＝360°×5＋222°，180°