初中数学湘教版九年级上册第2章 一元二次方程2.1 一元二次方程优质教案设计

第2章   一元二次方程

课题

 一元二次方程——小结与复习

本课（章节）需 12 课时 ，本节课为第 12 课时，为本学期总第 18 课时

教

学

目

标

1、掌握一元二次方程概念，

2、会选择适当的方法解一元二次方程；

3、掌握一元二次方程根的判别式和根与系数的关系及运用，

2．学会从数学的角度提出问题、理解问题，并能运用所学一元二次方程的相关知识解决问题．

重点

一元二次方程的解法与根的判别式，根与系数关系的正确理解与运用

难点

把实际问题转化为数学模型

主备教师

教具

多媒体

课型

新授

教   学   过   程

个案修改

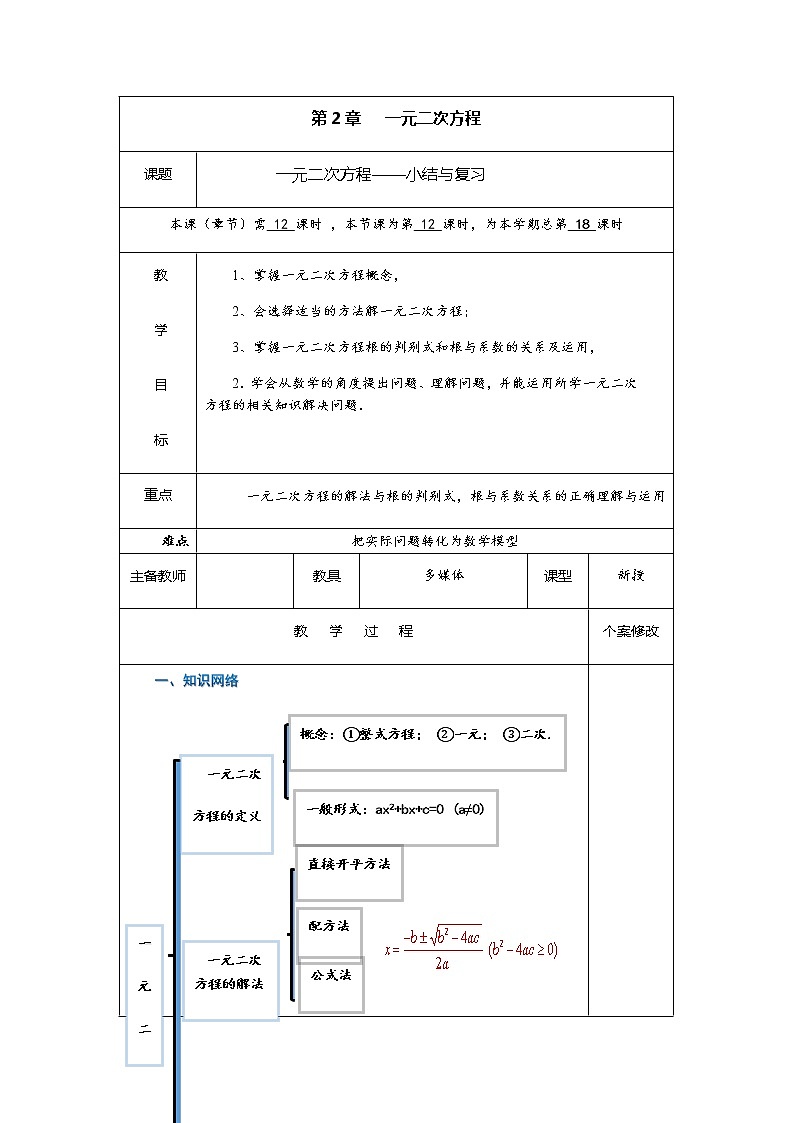
一、知识网络

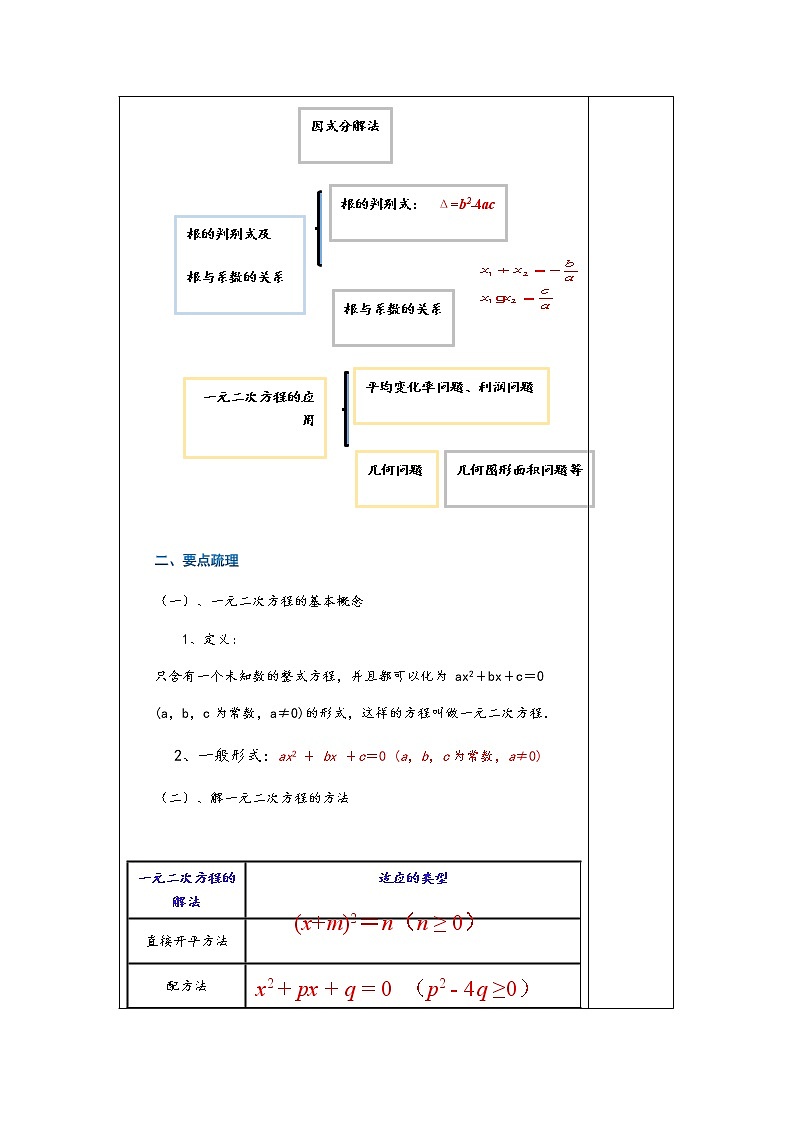
二、要点疏理

（一）、一元二次方程的基本概念

1、定义：

    只含有一个未知数的整式方程，并且都可以化为 ax2＋bx＋c＝0

(a，b，c为常数，a≠0)的形式，这样的方程叫做一元二次方程．

2、一般形式：ax2 ＋ bx ＋c＝0 (a，b，c为常数，a≠0)

（二）、解一元二次方程的方法

（三）、一元二次方程在生活中的应用

列方程解应用题的一般步骤：

1）审题：通过审题弄清已知量与未知量之间的数量关系．

2）设元：就是设未知数,分直接设与间接设,应根据实际需要恰当选取设元法．

3）列方程：就是建立已知量与未知量之间的等量关系．列方程这一环节最重要，决定着能否顺利解决实际问题．

4）解方程：正确求出方程的解并注意检验其合理性．

5）作答：即写出答语，遵循问什么答什么的原则写清答语．

三、专题讲练

例1 若关于x的方程(m-1)x2+mx-1=0是一元二次方程，则m的取值范围是（   ）

1. m≠1   B. m=1  C. m≥1  D. m≠0

例2 若关于x的一元二次方程（m-1)x2+x+m2-1=0有一个根为0,则m=       

例3 (1)用配方法解方程x2-2x-5=0时，原方程应变为（   ）

1.  (x-1)2=6    B.(x+2)2=9    C.  (x+1)2=6    D.(x-2)2=09

例4 已知关于x的一元二次方程x2-3m=4x有两个不相等的实数根，则m的取值范围是           

例5 已知一元二次方程x2－4x－3＝0的两根为m，n，求m2－mn＋n2．

例6 某机械公司经销一种零件，已知这种零件的成本为每件20元，调查发现当销售价为24元，平均每天能售出32件，而当销售价每上涨2元，平均每天就少售出4件.

 (1)若公司每天的销售价为x元，则每天的销售量为多少？

（2）如果物价部门规定这种零件的销售价不得高于每件28元，该公司想要每天获得150元的销售利润，销售价应当为多少元？

例7 菜农小王种植的某种蔬菜，计划以每千克5元的价格对外批发销售.由于部分菜农盲目扩大种植，造成该种蔬菜滞销.小王为了加快销售，减少损失，对价格经过两次下调后，以每千克3.2元的价格对外批发销售.求平均每次下调的百分率是多少？

例8  如图1，在宽为20米，长为32米的矩形地面上修筑同样宽的道路（图中阴影部分），余下的部分种上草坪．要使草坪的面积为540平方米，求道路的宽.

四、课堂小结，升华知识

教

学

反

思