(辅导班专用)人教版数学九年级暑假讲义+课堂小测(提高班)13《点和圆、直线和圆的位置关系》（2份打包，教师版+学生版）

第13讲    点和圆、直线和圆的位置关系

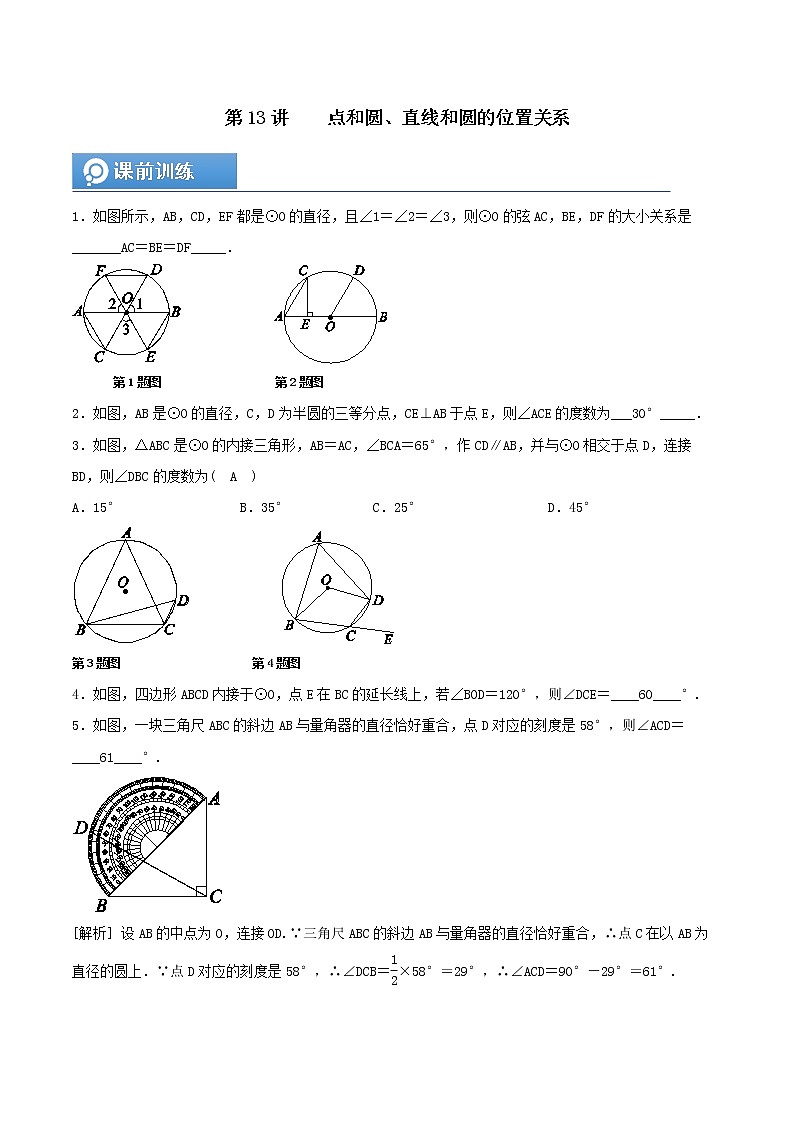
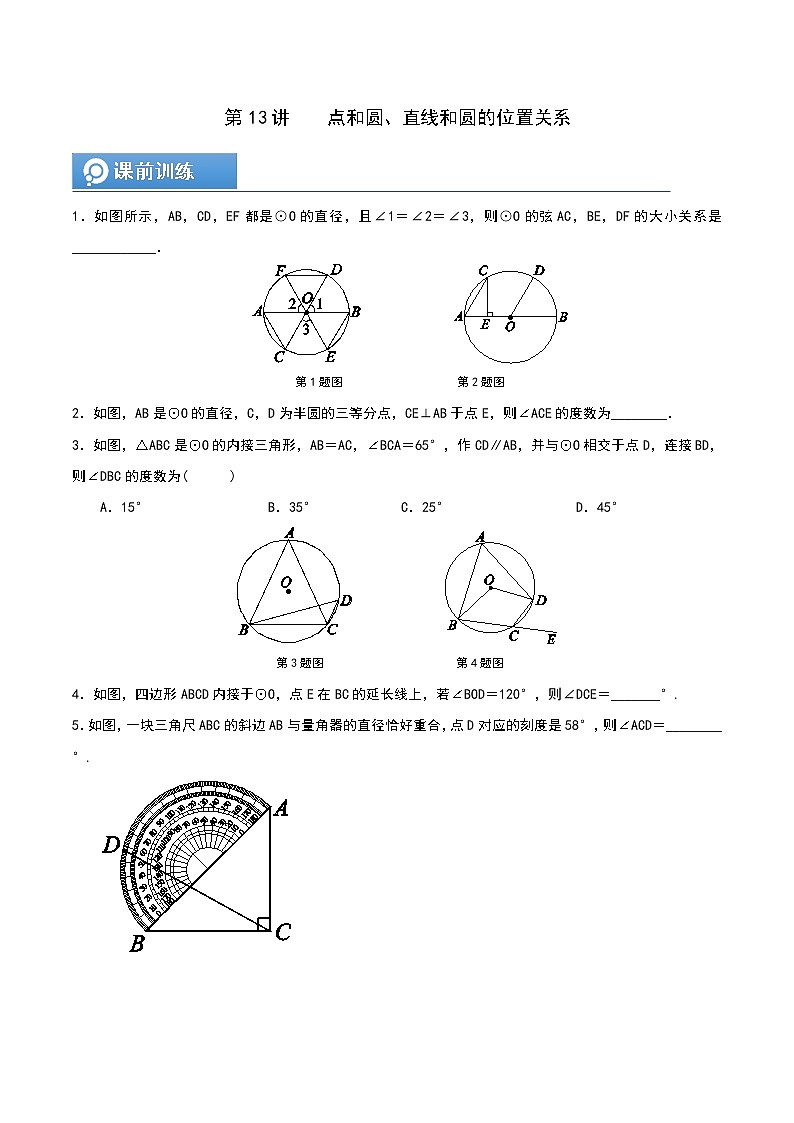
1．如图所示，AB，CD，EF都是⊙O的直径，且∠1＝∠2＝∠3，则⊙O的弦AC，BE，DF的大小关系是_______AC＝BE＝DF_____．

      第1题图                   第2题图

2．如图，AB是⊙O的直径，C，D为半圆的三等分点，CE⊥AB于点E，则∠ACE的度数为___30°_____．

3．如图，△ABC是⊙O的内接三角形，AB＝AC，∠BCA＝65°，作CD∥AB，并与⊙O相交于点D，连接BD，则∠DBC的度数为(　A　)

A．15°      B．35°            C．25°      D．45°

第3题图                      第4题图

4．如图，四边形ABCD内接于⊙O，点E在BC的延长线上，若∠BOD＝120°，则∠DCE＝____60____°.

5．如图，一块三角尺ABC的斜边AB与量角器的直径恰好重合，点D对应的刻度是58°，则∠ACD＝____61____°.

[解析] 设AB的中点为O，连接OD.∵三角尺ABC的斜边AB与量角器的直径恰好重合，∴点C在以AB为直径的圆上．∵点D对应的刻度是58°，∴∠DCB＝×58°＝29°，∴∠ACD＝90°－29°＝61°.

知识点一　点和圆的位置关系 

点和圆的位置关系有三种：点在圆外，点在圆上，点在圆内．

设圆的半径为r，点到圆心的距离为d，则点在圆外⇔d>r；点在圆上⇔d＝r；点在圆内⇔d<r.

说明：符号“⇔”读作“等价于”．“A⇔B”具有两方面的含义：一方面表示“A⇒B”，即由A推出B；另一方面表示“B⇒A”，即由B推出A.

注意：判断点和圆的位置关系，关键是先确定点到圆心的距离d和圆的半径r两个量，然后根据d和r的大小判断点和圆的位置关系．

知识点二　过已知点作圆 

过已知一点可作无数个圆；过已知两点也可作无数个圆；过不在同一条直线上的三点可以作一个圆，并且只能作一个圆．

温馨提示：判断三个点能不能确定一个圆，就是看这三个点在不在同一条直线上，经过同一条直线上的三个点不能作圆，不在同一条直线上的三个点能确定一个圆．

知识点三　三角形的外接圆与外心 

1．经过三角形的三个顶点可以作一个圆，这个圆叫做三角形的外接圆，这个三角形叫做这个圆的内接三角形．

2．外接圆的圆心是三角形三条边的垂直平分线的交点，叫做这个三角形的外心．

3.三角形的外心是三角形三条边的垂直平分线的交点，其中直角三角形的外心是斜边的中点，锐角三角形的外心在三角形的内部，钝角三角形的外心在三角形的外部．

知识点四　直线和圆的位置关系的判定与性质 

1．直线和圆有三种位置关系：相离、相切和相交．

(1)相交的定义：直线和圆有两个公共点，称这条直线和圆相交，这条直线叫做圆的割线．

(2)相切的定义：直线和圆只有一个公共点，称这条直线和圆相切，这条直线叫做圆的切线，这个点叫做切点．

(3)相离的定义：直线和圆没有公共点，称这条直线和圆相离．

2．直线和圆的位置关系的判定：设圆的半径为r，圆心到直线的距离为d，则直线与圆相交⇔d<r，直线与圆相切⇔d＝r，直线与圆相离⇔d>r.

温馨提示：(1)直线和圆的位置关系，可以用直线和圆的公共点的个数来判定，也可以用圆心到直线的距离(d)与半径(r)的大小关系来判定；(2)直线和圆的位置关系与点和圆的位置关系既有联系，又有区别，两者都是根据d与r的数量关系来判定图形的位置关系的，但前者中的d为圆心到直线的距离，后者中的d为点与圆心的距离．

1.1、已知⊙O的直径为10 cm，点P不在⊙O外，则OP的长(　　)

A．小于5 cm     B．不大于5 cm       C．小于10 cm     D．不大于10 cm

　[解析] ∵⊙O的直径为10 cm，∴⊙O的半径为5 cm.∵点P不在⊙O外，

∴点P在圆上或圆内，∴OP≤5 cm.

1.2、在平面直角坐标系中，⊙O的圆心在原点上，半径为2，则下列各点在⊙O上的是(　　)

A．(1，1)           B．(－1，)     C．(－2，－1)       D．(2，－2)

　[解析] A项，点(1，1)到圆心的距离是，＜2，故在圆内；B项，点(－1，)到圆心的距离为2，2＝2，故在圆上；C项，点(－2，－1)到圆心的距离为，＞2，故在圆外；D项，点(2，－2)到圆心的距离为2 ，2 ＞2，故在圆外．故选B.

1.3、如图,已知△ABC中,AC=3,AB=5,∠C=90°,以点C为圆心、r为半径作☉C.

(1)当r=3时,判断点A,B和☉C的位置关系;

(2)当r在什么范围时,点A在☉C内,点B在☉C外.

解:在△ABC中,AC=3,AB=5,∠C=90°,由勾股定理得BC=4.

(1)当r=3时,有r=AC,r<BC,点A在☉C上,点B在☉C外;

(2)当AC<r且BC>r,即3<r<4时,点A在☉C内,点B在☉C外.

1.4、8．如图，已知平面直角坐标系中，A(0，4)，B(4，4)，C(6，2)．

(1)写出经过A，B，C三点的圆弧所在圆的圆心M的坐标：(________，________)；

(2)判断点D(5，－2)与⊙M的位置关系.

解：(1)2　0

(2)∵⊙M的半径AM＝＝2 ，线段MD＝＝＜2 ，∴点D在⊙M内．

1.5、已知点P到⊙O上的点的最短距离为3 cm，最长距离为5 cm，则⊙O的半径为__________．

[答案] 1 cm或4 cm

[解析] 若点P在⊙O内，如图①.∵AP＝3 cm，BP＝5 cm，∴AB＝8 cm，∴OA＝4 cm；

若点P在⊙O外，如图②.∵AP＝3 cm，BP＝5 cm，∴AB＝2 cm，∴OA＝1 cm.

【变式训练1-1】如图，边长为1的正方形ABCD的对角线相交于点O，以点A为圆心，以1为半径画圆，则点O，B，C，D中，点________在⊙A内，点________在⊙A上，点________在⊙A外．

[答案] O　B，D　C

[解析]  ∵四边形ABCD为正方形，∴AC⊥BD，AO＝BO＝CO＝DO.

设AO＝BO＝x.由勾股定理，得AO2＋BO2＝AB2，即x2＋x2＝12，

解得x＝(负值已舍去)，∴AO＝＜1，AC＝＞1，

∴点O在⊙A内，点B，D在⊙A上，点C在⊙A外．

【变式训练1-2】在公园的O处附近有E，F，G，H四棵树，位置如图所示(图中小正方形的边长均相等)．现计划修建一座以点O为圆心，OA长为半径的圆形水池，要求池中不留树木，则E，F，G，H四棵树中需要被移除的为(　　)

A．E，F，G     B．F，G，H    C．G，H，E     D．H，E，F

[解析] ∵OA＝＝，OE＝2＜OA，∴点E在⊙O内∵OF＝2＜OA，∴点F在⊙O内．

∵OG＝1＜OA，∴点G在⊙O内．∵OH＝＝2 ＞OA，∴点H在⊙O外．

【变式训练1-3】如图，在矩形ABCD中，AB＝4，AD＝3，以顶点D为圆心作半径为r的圆，若要求另外三个顶点A，B，C中至少有一个点在圆内，且至少有一个点在圆外，则r的取值范围是__________.

[解析] 连接BD，在Rt△ABD中，AB＝4，AD＝3，则BD＝＝5.由题图可知3＜r＜5.

【变式训练1-4】如图,点A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为_____5______. 

【变式训练1-5】在同一平面内，⊙O 外一点P到⊙O 上的点的最大距离为6 cm，最小距离为2 cm，则⊙O 的半径为________ cm.

　[解析] ∵在同一平面内，⊙O 外一点P到⊙O上的点的最大距离为6 cm，最小距离为2 cm，

∴⊙O的直径为6－2＝4(cm)，∴⊙O的半径为2 cm.

2.1、如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,-2),则△ABC外接圆的圆心坐标是(　D　)

A.(2,3)      B.(3,2)      C.(1,3)    D.(3,1)

2.2、如图，若△ABC内接于半径为R的⊙O，且∠A＝60°，连接OB，OC，则边BC的长为(　　)

A.R       B.R          C.R       D.R

　[解析] 延长BO交⊙O于点D，连接CD，如图，则∠BCD＝90°，∠D＝∠A＝60°，

∴∠CBD＝30°.∵BD＝2R，∴DC＝R，∴BC＝R，故选D.

2.3、如图，在△ABC中，∠A＝60°，BC＝5 cm.能够将△ABC完全覆盖的最小圆形纸片的直径是________cm.

[答案]  [解析] 如图，能够将△ABC完全覆盖的最小圆形纸片是△ABC的外接圆⊙O.

连接OB，OC，则∠BOC＝2∠A＝120°.过点O作OD⊥BC于点D，则∠BOD＝∠BOC＝60°.

由垂径定理得BD＝BC＝ cm，∴OB＝2OD＝ cm，

∴能够将△ABC完全覆盖的最小圆形纸片的直径是 cm.

【变式训练2-1】如图，在平面直角坐标系xOy中，点A的坐标为(0，3)，点B的坐标为(2，1)，点C的坐标为(2，－3)，经画图操作，可知△ABC的外心的坐标应是(　　)

A．(0，0)       B．(1，0)          C．(－2，－1)        D．(2，0)

[解析] 如图．∵△ABC的外心即为三角形三边垂直平分线的交点，∴AB边的垂直平分线MN与BC边的垂直平分线EF的交点O′即为△ABC的外心，∴△ABC的外心的坐标是(－2，－1)．故选C.

【变式训练2-2】如图，AD为△ABC的外接圆⊙O的直径，若∠BAD＝50°，则∠ACB＝________°.

[解析] 连接BD，如图．∵AD为△ABC的外接圆⊙O的直径，∴∠ABD＝90°.

∴∠D＝90°－∠BAD＝90°－50°＝40°，∴∠ACB＝∠D＝40°.

【变式训练2-3】在Rt△ABC中，AB＝6，BC＝8，则这个三角形的外接圆的直径为(　　)

A．5       B．10        C．5或4      D．10或8

[解析] 直角三角形外接圆的直径是斜边，应分两种情况：当BC是斜边时，这个三角形的外接圆的直径为8；当AC是斜边时，AC＝＝＝10，则这个三角形的外接圆直径为10.故选D.

3.1、已知⊙O的半径为5 cm，圆心O到直线l的距离为5 cm，则直线l与⊙O的位置关系为(　B　)

A．相交      B．相切         C．相离      D．无法确定

3.2、如图，已知点A，B在半径为1的⊙O上，∠AOB＝60°，延长OB至点C，过点C作直线OA的垂线，记为l，则下列说法正确的是(　　)

A．当BC＝0.5时，l与⊙O相离      B．当BC＝2时，l与⊙O相切

C．当BC＝1时，l与⊙O相交         D．当BC≠1时，l与⊙O不相切

[解析] 若BC≠1，则OC＝OB＋BC≠2.∵∠AOB＝60°，∴∠ACO＝30°，

∴点O到直线l的距离＝OC≠1，∴l与⊙O不相切，故D正确．

3.3、如图，已知两个同心圆，大圆的半径为5，小圆的半径为3，若大圆的弦AB与小圆有公共点，则弦AB的取值范围是(　A　)

A．8≤AB≤10       B．8＜AB≤10      C．4≤AB≤5        D．4＜AB≤5

3.4、如图，∠APB＝30°，⊙O的半径为1 cm，圆心O在直线PB上，OP＝3 cm，若⊙O沿BP方向移动，当⊙O与直线PA相切时，圆心O移动的距离为__________．

[答案] 1 cm或5 cm[解析] 当⊙O与直线PA相切时，点O到PA的距离为1 cm.

∵∠APB＝30°，∴PO＝2 cm，∴圆心O移动的距离为3－2＝1(cm)或3＋2＝5(cm)．

3.5、如图所示，P为正比例函数y＝x的图象上的一个动点，⊙P的半径为3，设点P的坐标为(x，y)．

(1)求当⊙P与直线x＝2相切时，点P的坐标；

(2)请直接写出当⊙P与直线x＝2相交、相离时，x的取值范围．

解：(1)过点P作直线x＝2的垂线，垂足为A.

当点P在直线x＝2的右侧时，AP＝x－2＝3，∴x＝5，此时y＝×5＝，∴P；

当点P在直线x＝2的左侧时，AP＝2－x＝3，

∴x＝－1，此时y＝×(－1)＝－，

∴P.

综上所述，当⊙P与直线x＝2相切时，点P的坐标为或.

(2)当－1＜x＜5时，⊙P与直线x＝2相交；当x＜－1或x＞5时，⊙P与直线x＝2相离．

【变式训练3-1】已知⊙O的面积为9π cm2，若点O到直线l的距离为π cm，则直线l与⊙O的位置关系是(　　)

A．相交         B．相切      C．相离      D．无法确定

[解析] 依题意可知圆的半径为3 cm.∵圆心到直线的距离为π cm＞圆的半径3 cm，∴圆与直线相离，故选C.

【变式训练3-2】如图，在平面直角坐标系xOy中，半径为2的⊙P的圆心P的坐标为(－3，0)，将⊙P沿x轴正方向平移，使⊙P与y轴相切，则平移的距离为(　　)

A．1            B．1或5       C．3            D．5

[解析] 若⊙P位于y轴左侧且与y轴相切，则平移的距离为1；若⊙P位于y轴右侧且与y轴相切，则平移的距离为5.故选B。　

【变式训练3-3】在平面直角坐标系中，圆心P的坐标为(－3，4)，以r为半径在坐标平面内作圆：

(1)当r为何值时，圆P与坐标轴有1个交点？

(2)当r为何值时，圆P与坐标轴有2个交点？

(3)当r为何值时，圆P与坐标轴有3个交点？

(4)当r为何值时，圆P与坐标轴有4个交点？

解：(1)根据题意，得圆P和y轴相切，则r＝3.

(2)根据题意，得圆P和y轴相交，和x轴相离，则3<r<4.

(3)根据题意，得圆P和x轴相切或经过坐标原点，则r＝4或r＝5.

(4)根据题意，得圆P和x轴相交且不经过坐标原点，则r>4且r≠5.

【变式训练3-4】如图,直线AB,CD相交于点O,∠AOC=30°,半径为1 cm的☉P的圆心在直线AB上,开始时,PO=6 cm.如果☉P以1 cm/s的速度沿由A向B的方向移动,那么

(1)当☉P的运动时间t(s)满足什么条件时,☉P与直线CD相离?

(2)当☉P的运动时间t(s)满足什么条件时,☉P与直线CD相切?

(3)当☉P的运动时间t(s)满足什么条件时,☉P与直线CD相交?

解:当点P在射线OA上时☉P与CD相切,如图,过点P作PE⊥CD于点E,所以PE=1 cm.

因为∠AOC=30°,所以OP=2PE=2 cm.

所以☉P的圆心在直线AB上向右移动了6-2=4 cm后与CD相切.

所以☉P移动所用的时间是4÷1=4(s).

当点P在射线OB上时☉P与CD相切,如图,过点P作PF⊥CD于点F,所以PF=1 cm.

因为∠AOC=∠DOB=30°,所以OP=2PF=2 cm.

所以☉P的圆心在直线AB上向右移动了6+2=8 cm后与CD相切.

所以☉P移动所用的时间是8÷1=8(s).

所以(1)当☉P的运动时间t(s)满足条件0≤t<4或t>8时,☉P与直线CD相离;

(2)当☉P的运动时间t(s)满足条件t=4或t=8时,☉P与直线CD相切;

(3)当☉P的运动时间t(s)满足条件4<t<8时,☉P与直线CD相交.

1.如图,数轴上半径为1的☉O从原点O开始以每秒1个单位的速度向右运动,同时,距原点右边7个单位有一点P以每秒2个单位的速度向左运动,经过　2或　秒后,点P在☉O上. 

2.在Rt△ABC中,已知∠C=90°,BC=3,AC=4,以点B为圆心,3为半径作☉B,则

(1)AB的中点D,AC的中点E与☉B分别有怎样的位置关系?

(2)如果点A和点C有且只有一个点在☉B内,则☉B的半径应满足什么条件?

解:(1)因为∠C=90°,BC=3,AC=4,所以AB==5.

因为D为AB的中点,所以BD=2.5<3,所以点D在☉B内.

因为BE==>3,所以点E在☉B外.

(2)设☉B的半径为r,则r>BC且r≤BA,即当3<r≤5时,点A和点C有且只有一个点在☉B内.

3.如图,在平面直角坐标系xOy中,点A,B,P的坐标分别为(1,0),(2,5),(4,2).若点C在第一象限内,且横坐标、纵坐标均为整数,P是△ABC的外心,则点C的坐标为　(7,4)或(6,5)或(1,4)　. 

4.已知直线y＝kx(k≠0)经过点(12，－5)，将直线向上平移m(m＞0)个单位长度，若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点)，则m的取值范围为_______________．

[解析] 把(12，－5)代入y＝kx，得－5＝12k，∴k＝－.  由直线y＝－x向上平移m(m＞0)个单位长度后得到的直线l所对应的函数关系式为y＝－x＋m(m＞0)，设直线l与x轴、y轴分别交于点A，B，

当x＝0时，y＝m；当y＝0时，x＝m，∴A(m，0)，B(0，m)，

即OA＝m，OB＝m.在Rt△OAB中，AB＝＝＝m.

过点O作OD⊥AB于点D，如图所示．

∵S△ABO＝OD·AB＝OA·OB，∴OD·m＝·m·m，解得OD＝m.

由直线与圆的位置关系可知m＜6，解得0＜m＜.

5.已知直线y＝kx(k≠0)经过点(12，－5)，将直线向上平移m(m＞0)个单位长度，若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点)，则m的取值范围为__________.

[答案] 0＜m＜[解析] 如图，设平移后的直线与y轴、x轴分别交于点A，B.

易知直线AB的解析式为y＝－x＋m，∴A(0，m)，B(m，0)，AB＝＝m.

过点O作OC⊥AB于点C，则OC＝＝m.∵直线AB与半径为6的⊙O相交，∴OC＜6，即m＜6，

∴0＜m＜.

6.如图，已知⊙P的半径为2，圆心P在抛物线y＝x2－1上运动，当⊙P与x轴相切时，圆心P的坐标为______________．

[解析] 依题意，可设P(x，2)或P(x，－2)．

①当点P的坐标是(x，2)时，将其代入y＝x2－1，得2＝x2－1，

解得x＝±，此时P(，2)或(－，2)；

②当点P的坐标是(x，－2)时，将其代入y＝x2－1，得－2＝x2－1，即－1＝x2，此时方程无实数根．

综上所述，符合条件的点P的坐标是(，2)或(－，2)．

7.如图所示，要把破残的圆片复制完整，已知弧上的三点A，B，C.

(1)用尺规作图法找出所在圆的圆心；(保留作图痕迹，不写作法)

(2)设△ABC是等腰三角形，底边BC＝8 cm，腰AB＝5 cm.求圆片的半径R.

解：(1)分别作AB，AC的垂直平分线，设交点为O，则点O为所求圆的圆心．(作图略)

(2)连接AO，交BC于点E，连接OB.

∵AB＝AC，∴AE⊥BC，BE＝BC＝4.在Rt△ABE中，AE＝＝＝3.

在Rt△BEO中，OB2＝BE2＋OE2，即R2＝42＋(R－3)2，解得R＝.

即所求圆片的半径R为 cm.

8．如图，在Rt△ABC中，∠C＝90°，∠B＝60°，若AO＝x cm，⊙O的半径为1 cm，当x在什么范围内取值时，直线AC与⊙O相离、相切、相交？

解：过点O作OD⊥AC于点D.

∵∠C＝90°，∠B＝60°，∴∠A＝30°.

∵AO＝x cm，∴OD＝x cm.

(1)若⊙O与直线AC相离，则有OD>r，即x＞1，解得x＞2；

(2)若⊙O与直线AC相切，则有OD＝r，即x＝1，解得x＝2；

(3)若⊙O与直线AC相交，则有OD<r，即x＜1，解得x＜2，∴0<x<2.

综上可知：当x＞2时，直线AC与⊙O相离；当x＝2时，直线AC与⊙O相切；

当0＜x＜2时，直线AC与⊙O相交．

9.已知直线y＝kx(k≠0)经过点(12，－5)，将直线向上平移m(m＞0)个单位长度，若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点)，求出m的取值范围。

[解析] 把(12，－5)代入y＝kx，得－5＝12k，∴k＝－.

由直线y＝－x向上平移m(m＞0)个单位长度后得到的直线l所对应的函数关系式为y＝－x＋m(m＞0)，

设直线l与x轴、y轴分别交于点A，B，

当x＝0时，y＝m；当y＝0时，x＝m，∴A(m，0)，B(0，m)，

即OA＝m，OB＝m.在Rt△OAB中，AB＝＝＝m.

过点O作OD⊥AB于点D，如图所示．

∵S△ABO＝OD·AB＝OA·OB，∴OD·m＝·m·m，解得OD＝m.

由直线与圆的位置关系可知m＜6，解得0＜m＜.

10.如图，正方形ABCD的边长为8，M是AB的中点，P是BC边上的动点，连接PM，以点P为圆心，PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时，求BP的长.

解：由题意知BM＝4.分两种情况：

(1)当⊙P与CD相切时，设BP＝x，则PM＝PC＝8－x.

由勾股定理得x2＋42＝(8－x)2，解得x＝3；

(2)当⊙P与AD相切时，半径PM＝点P到AD的距离＝8.

由勾股定理得BP2＝82－42，解得BP＝4 (负值已舍)．

综上所述，BP的长为3或4 .

1.已知点P在半径为r的☉O外,点P与点O的距离为4,则r的取值范围是(　C　)

A.r>4        B.r≥4    C.r<4    D.r≤4

2.下列命题中真命题的个数是(　B　)

①过两点可以作无数个圆;

②经过三点一定可以作圆;

③任意一个三角形有一个外接圆,而且只有一个外接圆;

④任意一个圆只有一个内接三角形.

  A.1个      B.2个      C.3个     D.4个

3.☉O的半径为4,圆心到点P的距离为d,且d是方程x2-2x-8=0的根,则点P与☉O的位置关系是(　B　)

  A.点P在☉O内部    B.点P在☉O上       C.点P在☉O外部       D.点P不在☉O上

4.直线l与半径为r的⊙O相交，且点O到直线l的距离为6，则r的取值范围是(　　)

A．r＜6   B．r＝6   C．r＞6   D．r≥6

　[解析] ∵直线l与⊙O相交，∴圆心O到直线l的距离d＜r，即r＞d＝6.故选C.

5.如图,在△ABC中,O是它的外心,BC=24 cm,O到BC的距离是5 cm,则△ABC的外接圆的半径是　13　 cm. 

6.如图，△ABC内接于⊙O，AB为⊙O的直径，∠CAB＝60°，弦AD平分∠CAB，若AD＝6，则AC＝________．

[解析] 连接BD，如图．∵AB是直径，∴∠C＝∠D＝90°.

∵∠CAB＝60°，AD平分∠CAB，∴∠DAB＝∠CBA＝30°.

设BD＝x，则AB＝2x.在Rt△ADB中，∵AD＝6，AB2＝AD2＋BD2，

∴(2x)2＝62＋x2，解得x＝2 ，∴AB＝4 ，∴AC＝2 .

7.如图，在矩形ABCD中，AB＝4，AD＝3，以顶点D为圆心作半径为r的圆，若要求另外三个顶点A，B，C中至少有一个点在圆内，且至少有一个点在圆外，则r的取值范围是________．

[解析] 如图，连接BD.在矩形ABCD中，AD＝3，CD＝AB＝4，在Rt△ABD中，BD＝＝＝5，∴AD＜CD＜BD.若点A一定在圆内，则r＞3；若点B一定在圆外，则r＜5，故r的取值范围为3＜r＜5.

8．⊙O的半径为R，点O到直线l的距离为d，R，d是关于x的方程x2－4x＋m＝0的两根，当直线l与⊙O相切时，m的值为________．

　[解析] ∵R，d是关于x的方程x2－4x＋m＝0的两根，且直线l与⊙O相切，∴d＝R，∴方程有两个相等的实数根，∴Δ＝b2－4ac＝16－4m＝0，解得m＝4.故答案为4.

9.如图，⊙O的半径OC＝5 cm，直线l⊥OC，垂足为H，且l交⊙O于A，B两点，AB＝8 cm，若l沿OC所在直线平移后与⊙O相切，则平移的距离是(　　)

A．1 cm    B．2 cm        C．8 cm     D．2 cm或8 cm

[解析] 如图，连接OB.∵AB⊥OC，∴AH＝BH，∴BH＝AB＝×8＝4(cm)．

在Rt△BOH中，OB＝OC＝5 cm，∴OH＝＝＝3(cm)．

∵直线l通过平移与⊙O相切，∴直线l垂直于过点C的直径，垂足为直径的两个端点，∴当直线l向下平移时，平移的距离＝5－3＝2(cm)；当直线l向上平移时，平移的距离＝5＋3＝8(cm)．

10．以坐标原点O为圆心，作半径为2的圆，若直线y＝－x＋b与⊙O相交，则b的取值范围是(　　)

A．0≤b＜2      B．－2 ≤b≤2

C．－2 <b<2     D．－2 ＜b＜2

[解析] 当直线y＝－x＋b与⊙O相切，且经过第一、二、四象限时，如图．

在y＝－x＋b中，当x＝0时，y＝b，则点B的坐标是(0，b)，当y＝0时，x＝b，

则点A的坐标是(b，0)，则OA＝OB，即△OAB是等腰直角三角形．

连接圆心O和切点C.则OC＝2，OC⊥AB.故OB＝OC＝2 ，即b＝2 ；

同理，当直线y＝－x＋b与⊙O相切，且经过第二、三、四象限时，b＝－2 .

故若直线y＝－x＋b与⊙O相交，则b的取值范围是－2 ＜b＜2 .故选D.