2022北京市.通州区毕业年级学考模拟测试数学试卷有答案

这是一份2022北京市.通州区毕业年级学考模拟测试数学试卷有答案，共15页。试卷主要包含了选择题，填空题，解答题．等内容，欢迎下载使用。
通州区2022年毕业年级学考模拟测试
数学试卷 2022年4月
考生须知
1．本试卷共8页，三道大题，28道小题，满分100分.考试时间120分钟.
2．在试卷、答题卡上准确填写学校名称、班级、姓名.
3．试题答案一律书写在答题卡上各题指定区域内的相应位置上.
4．请用蓝色或黑色钢笔、圆珠笔答卷．
5．考试结束，请将本试卷和答题卡一并交回.
一、选择题(本题共16分，每小题2分)
1. 下列几何体中，其俯视图是三角形的是



A B C D
2. 2022年3月，在第十三届全国人民代表大会第五次会议上，国务院总理李克强在政府工作报告中指出:2021年，我国经济保持恢复发展，国内生产总值达到1140000亿元，增长8.1%. 将1140000用科学记数法表示应为
A．0.114×107 B．1.14×107 C．1.14×106 D．11.4×105
3．2022年北京和张家口成功举办了第24届冬奥会和冬残奥会．下面关于奥运会的剪纸图片中是轴对称图形的是



A B C D
4. 实数a在数轴上的对应点的位置如图所示，那么下列结论正确的是

A． B．-a 0 D．
5．如果甲、乙、丙三位同学随机站成一排，那么甲站在中间的概率是
A． B． C． D．
6．如图，已知，那么的度数为



A．60° B．120° C．130° D．150°
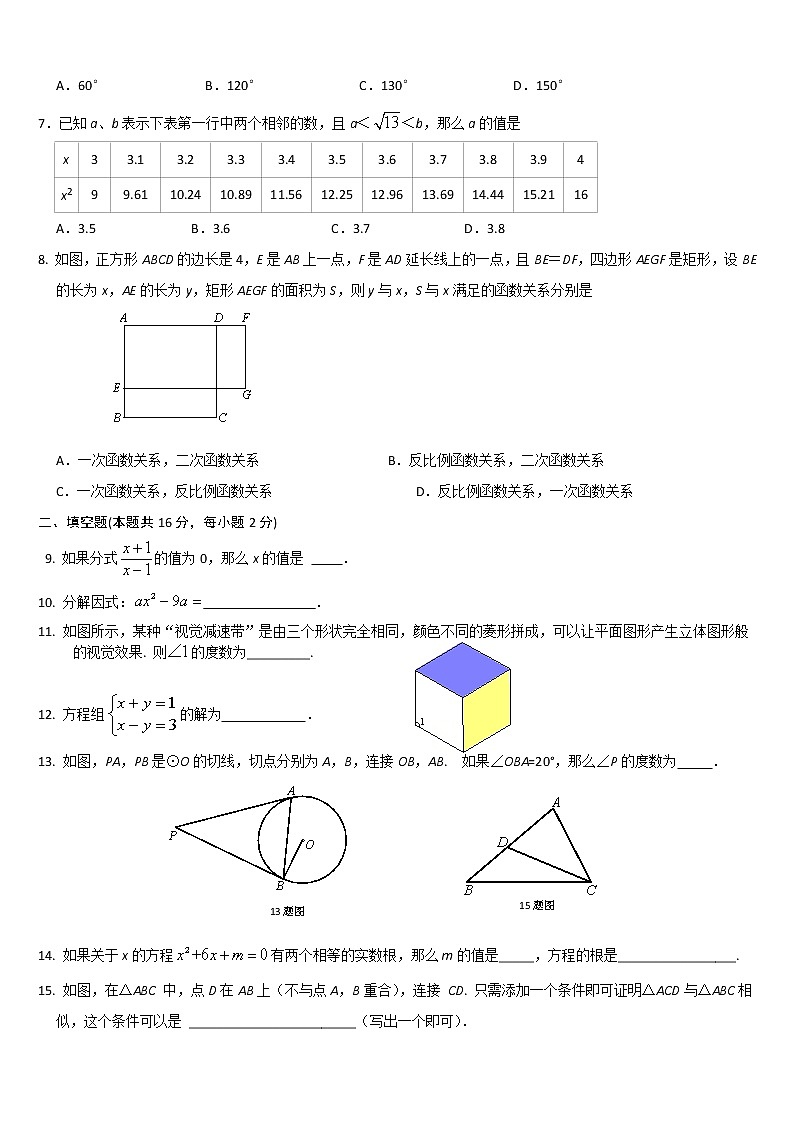
7．已知a、b表示下表第一行中两个相邻的数，且a＜＜b，那么a的值是
x
3
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
4
x2
9
9.61
10.24
10.89
11.56
12.25
12.96
13.69
14.44
15.21
16
A．3.5 B．3.6 C．3.7 D．3.8
8. 如图，正方形ABCD的边长是4，E是AB上一点，F是AD延长线上的一点，且BE＝DF，四边形AEGF是矩形，设BE的长为x，AE的长为y，矩形AEGF的面积为S，则y与x，S与x满足的函数关系分别是

A．一次函数关系，二次函数关系 B．反比例函数关系，二次函数关系
C．一次函数关系，反比例函数关系 D．反比例函数关系，一次函数关系
二、填空题(本题共16分，每小题2分)
9. 如果分式的值为0，那么x的值是 　 　．
10. 分解因式：　 　．
11. 如图所示，某种“视觉减速带”是由三个形状完全相同，颜色不同的菱形拼成，可以让平面图形产生立体图形般
的视觉效果. 则的度数为_________.

12. 方程组的解为　 　．
13. 如图，PA，PB是⊙O的切线，切点分别为A，B，连接OB，AB. 如果∠OBA=20°，那么∠P的度数为 ．
15题图
13题图


14. 如果关于x的方程有两个相等的实数根，那么m的值是_____，方程的根是_________________.
15. 如图，在△ABC 中，点D在AB上（不与点A，B重合），连接 CD. 只需添加一个条件即可证明△ACD与△ABC相似，这个条件可以是 ________________________（写出一个即可）．
16. 某学习兴趣小组由学生和教师组成，人员构成同时满足以下三个条件：
（ⅰ）男学生人数多于女学生人数；
（ⅱ）女学生人数多于教师人数；
（ⅲ）教师人数的两倍多于男学生人数．
① 若教师人数为4，则女学生人数的最大值为 ；
② 该小组人数的最小值为 ．
三、解答题（本题共68分，第17-20题，每题5分，第21-22题，每题6分，第23-24题，每5分，第25-26题，每题6分，第27-28题，每题7分）解答应写出文字说明、演算步骤或证明过程）．
17. 计算：.


18. 解不等式组.


19．已知，求代数式的值．




20．已知：如图，△ABC为锐角三角形，AB＝AC．
求作：点P，使得，且.
作法：①以点A为圆心，AB长为半径画圆；
②以点B为圆心，BC长为半径画弧，交⊙A于点D（异于点C）；
③连接DA并延长交⊙A于点P．
所以点P就是所求作的点．
（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
（2）完成下面的证明．
证明：连接PC.
∵，
∴点C在⊙A上．
又∵，
∴（___________________________）（填推理的依据），
由作图可知，，
∴．
∴．
21．已知一次函数的图象与反比例函数的图象交于A，B两点．
（1）当点A的坐标为（2，1）时.
①求m，k的值；②当时，_____（填“>”，“=”或“”或者“ . ………………… 3分
（2）∵一次函数的图象沿y轴向下平移4个单位长度后，
∴ 平移后的表达式为， ………………… 4分
∵点A，B关于原点对称，
∴的图象经过原点， ………………… 5分
∴，
∴. ………………… 6分
22． （1）证明：∵AB＝BC，BD平分，
∴AD=CD， ………………… 1分
∵E为AB的中点，
∴DE是△ABC的中位线，
∴DE∥CF， ………………… 2分
∵EF∥BD，
∴四边形DEFB是平行四边形. ………………… 3分
（2）解：∵AB＝BC，BD平分，
∴AC⊥BD，
∵，，
∴ . ………………… 4分
∵E为AB的中点，
∴ . ………………… 5分
∵四边形DEFB是平行四边形，
∴ .
∵AB＝BC，
∴ .
∴. ………………… 6分
23. 解：（1）3.99 ………………… 1分
（2）






………………… 3分
（3）是 ………………… 5分
24. （1）2021年我国各省、直辖市、自治区粮食产量的中位数为1421.2 万吨 …………… 1分
（2）>，< ………………… 3分
（3）. ………………… 4分
2022年全国粮食总产量约为13930亿斤. ………………… 5分
25．（1）证明：连接OC，
∵CD是⊙O的切线，
∴∠OCD＝，
∴∠ACO+∠ACD＝， ………………… 1分
∵AB是⊙O的直径，
∴∠ACB＝，
∵∠CAB+∠B＝，
∵OA=OC，
∴∠ACO=∠CAB，
∴∠DCA＝∠B. ………………… 2分
（2）解：∵CD是⊙O的切线，
∴∠OCD＝，
∵∠D＝30°，
∴∠COD＝，
∵
∴∠B＝30°， ………………… 3分
∵AB是⊙O的直径，CE⊥AB，
∴
∴∠AOC＝∠AOF＝，
∴∠BOG=∠AOF＝， ………………… 4分
∴， ………………… 5分
∴ ，
∴，
∴. ………………… 6分
26．解：（1）当时，
∴. ………………… 1分
（2）∵对称轴是直线，
∴顶点B的坐标为 （，）.
点关于对称轴的对称点为.
当时，
∴. ………………… 2分
当时，
∴. ………………… 3分
当，时
y随x的增大而减小，
∴，
∵
∴，
∴， ………………… 4分
当，时，
y随x的增大而增大，
∴，
∵
∴，
∴， ………………… 5分
∴的取值范围是或. ………………… 6分
27．（1）①的度数是； ………………… 1分
②证明： ∵，，
∴，
∵，
∴ , ………………… 2分
∵ EF∥BD，
∴.
∴.
∴. ………………… 3分
（2）线段AF和CD的数量关系是.
证明：延长EF交AC于点G. ………………… 4分
∵ ，
∴，， ………………… 5分
∴
在△DCA和△AGE中，
，
∴△DCA ≌△AGE， ………………… 6分
∴
∵
∴. ………………… 7分
∴.
证法二：在AC上截取CH=CD，连接DH . 证△DHA ≌△AFE .
28. 解：（1） ①原点O到线段AB上一点的最大距离为2，最小距离为1； ………………… 2分
② 当时，符合题意 ………………… 3分
当时；
连接AC ，过点O作OE ⊥AC于点E .
在Rt△COE中，OC=1，
∴OE < OC.
∴不符合题意. ………………… 4分
当时；如图，
连接AC ，过点O作OE ⊥AC于点E .
在Rt△ADC中，
∴ .
∴ .
在Rt△OEC中，
∴.
∴.
∴符合题意
当，时，都不符合题意.
∴的取值范围为或. ………………… 5分
（3）当点O与等边的一边共线时（如下图），
的“全距”为








当等边的一个顶点在线段OM的延长线时（如下图），
的“全距”为





∴的“全距”d的取值范围为. ………………… 7分