2022年广东省清远市清城区九年级下学期一模数学试题（附答案）

这是一份2022年广东省清远市清城区九年级下学期一模数学试题（附答案），共17页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
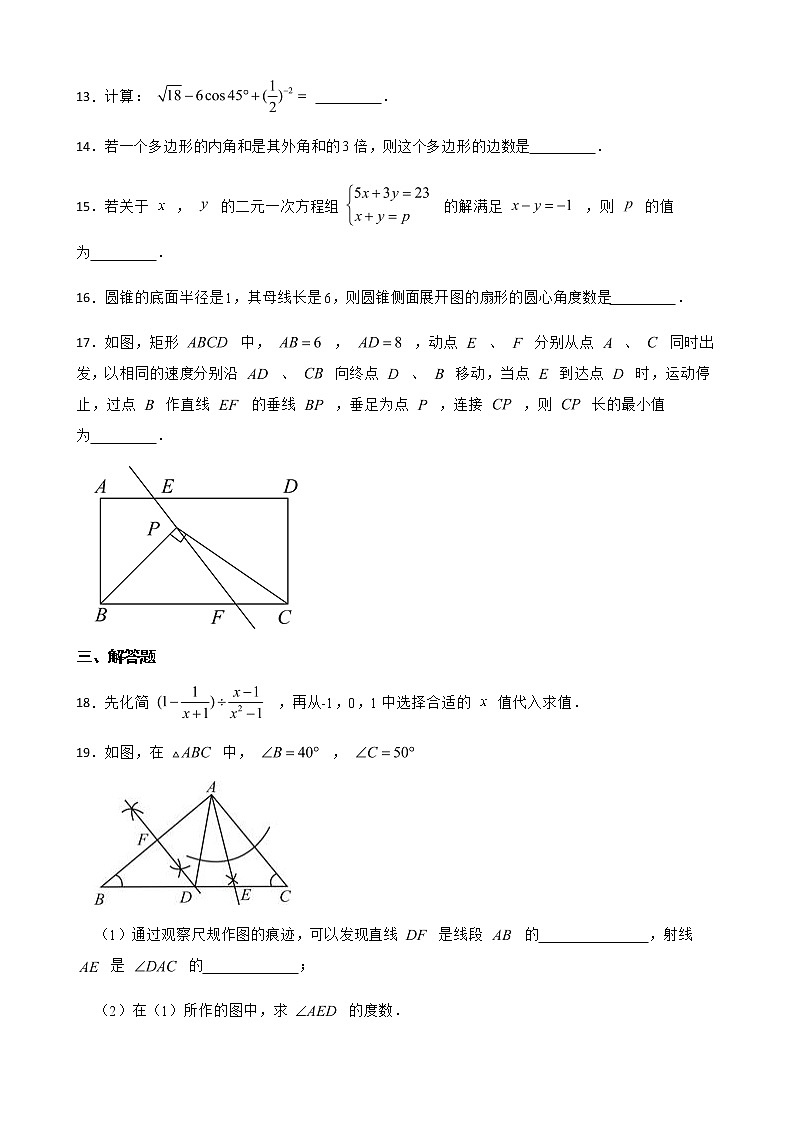
 九年级下学期一模数学试题一、单选题1．下列四个数中，绝对值最大的是（　　）  A．1 B．0.3 C． D．-32．新型冠状病毒呈球形或椭圆形，有包膜，直径大约是 ，属于第七种冠状病毒，将 用科学记数法表示为（　　）  A． B． C． D．3．若 ，则 （　　）  A．-3 B．6 C．-6或6 D．-64．下列运算正确的是（　　）  A． B．C． D．5．在平面直角坐标系中，点 与点 关于 对称，则 的值为（　　）  A．1 B．3或1 C．-3或1 D．3或-16．如图，平行四边形 中， ，点 在 上，且 ，则 的度数是（　　）  A． B． C． D．7．不等式组 的最小整数解是（　　）  A．-1 B．0 C．2 D．38．广东2021年的高考采用“ ”模式：“3”是指语文、数学、外语3科为必选科目，“1”是指在物理、历史2科中任选1科，“2”是指在化学、生物、思想政治、地理4科中任选2科．若小华在“1”中选了物理，则他在“2”中选化学、生物的概率是（　　）  A． B． C． D．9．若点 ， 在反比例函数 的图象上，且 ，则 的取值范围是（　　）  A． B．C． D． 或 10．如图，已知等边三角形 绕点 顺时针旋转 得 ，点 、 分别为线段 和线段 上的点，且 ，则下列结论正确的有（　　）  ① ；② 为等边三角形；③若把 、 、 、 四边的中点相连，则得到的四边形是矩形；④若 ， ，则 A．4个 B．3个 C．2个 D．1个二、填空题11．分解因式x2y－2xy＋y＝　        　12．把抛物线 向右平移1个单位长度，再向上平移2个单位长度，得到的抛物线的解析式为　           　．  13．计算： 　     　．  14．若一个多边形的内角和是其外角和的3倍，则这个多边形的边数是　     　．15．若关于 ， 的二元一次方程组 的解满足 ，则 的值为　     　．  16．圆锥的底面半径是1，其母线长是6，则圆锥侧面展开图的扇形的圆心角度数是　     　．17．如图，矩形 中， ， ，动点 、 分别从点 、 同时出发，以相同的速度分别沿 、 向终点 、 移动，当点 到达点 时，运动停止，过点 作直线 的垂线 ，垂足为点 ，连接 ，则 长的最小值为　     　．  三、解答题18．先化简 ，再从-1，0，1中选择合适的 值代入求值．  19．如图，在 中， ， （1）通过观察尺规作图的痕迹，可以发现直线 是线段 的　           　，射线 是 的　         　；  （2）在（1）所作的图中，求 的度数．  20．2021年秋季教育部提出政策要求，初中书面作业平均完成时间不超过90分钟，学生每天的完成作业时长不能超过2小时，某中学为了积极推进教育部的新政策实施，对本校学生的作业情况进行了抽样调查，统计结果如图所示：（1）这次抽样共调查了 ▲ 名学生，并补全条形统计图：（2）计算扇形统计图中表示作业时长为1小时对应的扇形圆心角的度数；（3）若该中学共有学生2000人，请估计该校作业时间不超过2小时的学生人数．21．如图①，将“欢迎光临”门挂便斜放置时，测得挂绳的一段 cm.另一段 cm.已知两个固定扣之间的距离 cm  （1）求点 到 的距离；  （2）如图②，将该门挂扶“正”（即 ），求 的度数.（参考数据： ， ， ， ， ）  22．某汽车贸易公司销售 ， 两种型号的新能源汽车， 型车每台进货价格比 型车每台进货价格少3万元，该公司用24万元购买 型车的数量和用30万元购买 型车的数量相同．  （1）求购买一台 型、一台 型新能源汽车的进货价格各是多少万元？  （2）该公司准备用不超过300万，采购 ， 两种新能源汽车共22台，问最少需要采购 型新能源汽车多少台？  23．如图，一次函数 的图象与反比例函数 的图象交于点 ，与 轴交于点 ，过点 作 轴，垂足为 ，若 ．  （1）求点 的坐标及 的值：  （2）若 ，求一次函数的表达式．  24．如图，在菱形 中， 是对角线 上一点 ， ，垂足为 ，以 为半径的 分别交 于点 ，交 的延长线于点 ， 与 交于点 ．  （1）求证： 是 的切线；  （2）若 是 的中点， ， ．  ①求 的长；②求菱形 的面积．25．如图，二次函数y= x2+bx+c的图象与x轴交于A（3，0），B（-1，0），与y轴交于点C．若点P，Q同时从A点出发，都以每秒1个单位长度的速度分别沿AB，AC边运动，其中一点到达端点时，另一点也随之停止运动．（1）求该二次函数的解析式及点C的坐标；（2）当点P运动到B点时，点Q停止运动，这时，在x轴上是否存在点E，使得以A，E，Q为顶点的三角形为等腰三角形？若存在，请求出E点坐标；若不存在，请说明理由． （3）当P，Q运动到t秒时，△APQ沿PQ翻折，点A恰好落在抛物线上D点处，请判定此时四边形APDQ的形状，并求出D点坐标．答案解析部分1．【答案】D2．【答案】C3．【答案】D4．【答案】B5．【答案】C6．【答案】A7．【答案】B8．【答案】A9．【答案】C10．【答案】A11．【答案】12．【答案】13．【答案】414．【答案】815．【答案】616．【答案】60°17．【答案】418．【答案】解：化简，得：原式 ，  ∵题中分式有意义，∴ ， ， ，∴有 ，则在-1，0，1三个数中只能选择 ，将 代入化简后的代数式．得：原式=019．【答案】（1）垂直平分线；角平分线（2）解：∵DF是线段AB的垂直平分线， ∴DB=DA，∴∠BAD=∠B=40°，∵∠B=40°，∠C=50°，∴∠BAC=90°，∴∠DAC=50°．∵射线AE是∠DAC的平分线，∴∠DAE=25°=∠EAC．∴∠AED=∠EAC+∠C=25°+50°=75°．20．【答案】（1）解：500；据图可知，需要1.5小时完成作业的学生有占总数的比率为36%， 则需要1.5小时完成作业的学生人数为： （人），条形图补全如下：（2）解：需要1小时完成作业的学生有100人占总数的比率为 ，  则其在扇形统计图中对应的圆心角的度数为： ；（3）解：样本中，处理作业不超过2小时的学生数为：100+180=280（人）， 则其在样本中所占比率为： ，运用样本估算总体，则全校作业时间不超过2小时的学生人数为： （人）．21．【答案】（1）解：过点 作 于点 ，如图.  设 ，则 .∵ ， ， ，∴ ，即 ，解得 ，∴ .（2）解：由已知，得 .  ∵ ， ，∴ ，∴ ，∴ .22．【答案】（1）解：设A型新能源车的进货价格为x万元，B型新能源车的进货价格为y万元， 根据题意，得： ，解得： ，经检验，方程组的解符合题意，即：A型新能源车的进货价格为12万元，B型新能源车的进货价格为15万元；（2）解：设公司计划购买A型新能源车m台，则B型新能源车的购买量为(22-m)台， 根据题意，有： ，解不等式得： ，即：最少需要购买A型新能源车10台．23．【答案】（1）解：令y=0，则kx- 3k= 0， 出x= 2，A(3，0)，设C(a，b)，∵CB⊥y轴，B (0，b)，∴ BC= -a，∵S△ABC=3， ×(-a)·b=3，∴ ab=-6，m- 1=ab=-6，∴m=-5，即A(3，0)， m= -5；（2）解：在Rt△AOB中，AB2=0A2 + OB2， AB=  ，∴b2+9=18，b2=9，b=±3，∵b> 0，∴b=3，∴a=-2，∴C(-2，3)，将C(-2， 3)代入到直线解析式中得-2k-3k= 3，解得k=- ∴一次函数的表达式为y= 24．【答案】（1）证明：过O作OM⊥BC于M， ∵BD是菱形ABCD的对角线，∴∠ABD=∠CBD∵OM⊥BC，OE⊥AB∴OE=OM∴BC是⊙O的切线．（2）解：①如图， ∵G是OF的中点，OF=OH，∴OG= ∵AB∥CD，OE⊥AB，∴OF⊥CD∴∠OGH=90°∴sin∠GHO= '∴∠GHO=30°∴∠GOH=60°∴∠HOE=120°∵OG=4，∴OH=8由弧长公式得到   的长∶  ；②·如图，过A作AN⊥BD于N，∵四边形ABCD是菱形∴DN=NB= ，AB∥CD，∠CDB=∠ADB∴∵ ， ，OE=OH=8∴OD=   ，OB=   ，DN= ∵∠CDB=∠ADB，∠AND=∠DGO=90°∴△DGO∽△AND∴ ，即 ∴∴ ．25．【答案】（1）解：∵二次函数y= x2+bx+c的图象与x轴交于A（3，0），B（-1，0）， ∴ ，解得 ，∴y= x2- x-4．∴C（0，-4）（2）解：存在． 如图1，过点Q作QD⊥OA于D，此时QD∥OC，∵A（3，0），B（-1，0），C（0，-4），O（0，0），∴AB=4，OA=3，OC=4，∴AC= =5，∵当点P运动到B点时，点Q停止运动，AB=4，∴AQ=4．∵QD∥OC，∴ ，∴ ，∴QD= ，AD= ．①作AQ的垂直平分线，交AO于E，此时AE=EQ，即△AEQ为等腰三角形，设AE=x，则EQ=x，DE=AD-AE=| -x|，∴在Rt△EDQ中，（ -x）2+（ ）2=x2，解得 x= ，∴OA-AE=3- =- ，∴E（- ，0），说明点E在x轴的负半轴上；②以Q为圆心，AQ长半径画圆，交x轴于E，此时QE=QA=4，∵ED=AD= ，∴AE= ，∴OA-AE=3- =- ，∴E（- ，0）．③当AE=AQ=4时，当E在A点左边时，∵OA-AE=3-4=-1，∴E（-1，0）．当E在A点右边时，∵OA+AE=3+4=7，∴E（7，0）．综上所述，存在满足条件的点E，点E的坐标为（- ，0）或（- ，0）或（-1，0）或（7，0）．（3）   解：四边形APDQ为菱形，D点坐标为（- ，- ）．理由如下：如图2，D点关于PQ与A点对称，过点Q作，FQ⊥AP于F，∵AP=AQ=t，AP=DP，AQ=DQ，∴AP=AQ=QD=DP，∴四边形AQDP为菱形，∵FQ∥OC，∴ ，∴ ，∴AF= t，FQ= t，∴Q（3- t，- t），∵DQ=AP=t，∴D（3- t-t，- t），∵D在二次函数y= x2- x-4上，∴- t= （3- t）2- （3- t）-4，∴t= ，或t=0（与A重合，舍去），∴D（- ，- ）．